Angle of Depression - Definition, Formula & Problems

Edited By Team Careers360 | Updated on Jul 02, 2025 05:13 PM IST

The angle of depression is an angle formed by a horizontal line and a line of sight from a higher point to a lower point. It is used to describe the angle at which an object is viewed from above. For example, if you are standing on top of a hill and looking down at an object on the ground below, the angle of depression would be the angle between the horizontal line and the line of sight from your eyes to the object.

This Story also Contains

Opposite of depression
Depression meaning in geography
Depression in Hindi
Depression Meaning
How to find the angle of elevation and depression
Pictures that represent depression, the height of the depression

The angle of depression can be measured in degrees using a protractor or other angle-measuring tool. It is often used in trigonometry and geometry to solve problems involving angles and distances, such as finding the distance to an object based on its angle of depression.

In real-world applications, the angle of depression is often used in surveying, aviation, and navigation to measure the angle at which an object is viewed from above. It can also be used in engineering and construction to determine the slope of a surface or the height of an object.

Opposite of depression

Depression is a common mental health disorder characterized by persistent feelings of sadness, hopelessness, and a lack of interest or pleasure in activities. It can cause significant distress and interfere with daily functioning.

The opposite of depression is often described as being in a state of well-being or happiness. This can include feeling content, satisfied, and fulfilled, as well as having a positive outlook on life and a sense of purpose.

While it is not uncommon to experience occasional feelings of sadness or low mood, depression is different in that it is a persistent and often severe condition that can last for weeks, months, or even years. It can also cause physical symptoms such as fatigue, changes in appetite, and difficulty concentrating.

If you are experiencing symptoms of depression, it is important to seek help from a mental health professional. Treatment options may include therapy, medication, or a combination of both. With proper treatment, it is possible to manage and overcome depression and improve your overall well-being.

Depression meaning in geography

In geography, the term "depression" can refer to a low-lying area or a landform that is lower in elevation than the surrounding area. This can include natural features such as valleys, basins, and sinkholes, as well as man-made features such as quarries and pits.

Depressions can be formed through a variety of geological processes, including tectonic activity, erosion, and sedimentation. They can range in size from small, shallow features to large, deep basins.

In some cases, depressions can serve as important habitats for a variety of plant and animal species, particularly if they contain water or other resources. They can also be important sources of minerals and other natural resources, as well as being used for agriculture and other human activities.

It is important to note that the term "depression" in geography is unrelated to the mental health disorder of the same name. The mental health disorder of depression is characterized by persistent feelings of sadness and hopelessness, while depression in geography refers to a low-lying area or landform.

Depression in Hindi

In Hindi, the word "depression" (डिप्रेशन) refers to a mental health disorder characterized by persistent feelings of sadness, hopelessness, and a lack of interest or pleasure in activities. It can cause significant distress and interfere with daily functioning.

Depression is a common mental health condition that can affect people of all ages and backgrounds. It can be caused by a variety of factors, including genetics, life events, and physical health problems.

If you or someone you know is experiencing symptoms of depression, it is important to seek help from a mental health professional. Treatment options may include therapy, medication, or a combination of both. With proper treatment, it is possible to manage and overcome depression and improve overall well-being.

Depression Meaning

A mental health condition called depression is characterized by protracted feelings of melancholy, hopelessness, and a lack of enthusiasm for or enjoyment from activities. It can be extremely upsetting and interfere with day-to-day activities.

A persistently depressed mood can include feelings of sadness, anxiety, or emptiness; feelings of hopelessness or pessimism; a loss of interest or pleasure in once-enjoyable activities; difficulty focusing, remembering details, or making decisions; changes in appetite and sleep patterns; exhaustion or a lack of energy; and thoughts of death or suicide. People of different ages and socioeconomic backgrounds may be affected by depression, a prevalent mental health problem. Several things, including as genetics, life events, and physical health issues, can contribute to its occurrence.

A mental health expert should be consulted if you are exhibiting signs of depression. Therapy, medication, or a combination of the two may be used as a form of treatment. With the right care, depression may be controlled, conquered, and one's general wellbeing enhanced.

How to find the angle of elevation and depression

To find the angle of elevation or depression, you will need to use a bit of trigonometry. Here are the steps to follow:

Draw a diagram to represent the situation. The angle of elevation or depression is formed by a horizontal line and a line of sight from a higher or lower point.
Measure the distance between the two points. This is called the "horizontal distance."
Measure the height difference between the two points. If the higher point is above the lower point, this is the "height." If the lower point is above the higher point, this is the "depth."
Use the trigonometric functions sine, cosine, or tangent to find the angle. For example, if you are trying to find the angle of elevation, you can use the following formula:

angle = sin^(-1)(height/horizontal distance)

If you are trying to find the angle of depression, you can use the following formula:

angle = sin^(-1)(depth/horizontal distance)

Convert the result from radians to degrees if necessary. One full rotation is equal to 360 degrees, so to convert from radians to degrees, you can use the following formula:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

degrees = radians * (180/pi)

It may be helpful to use a calculator or a trigonometry reference chart to help you solve these equations.

Pictures that represent depression, the height of the depression

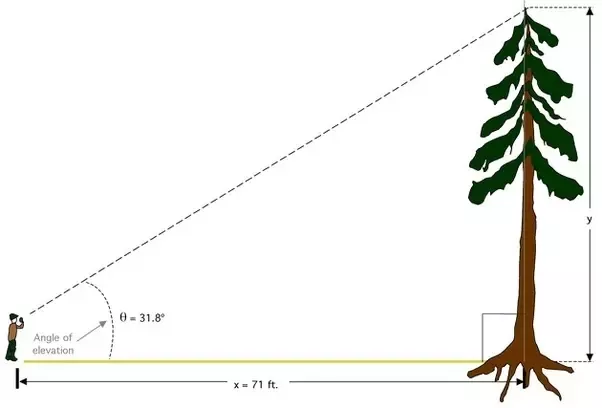
1706366538606

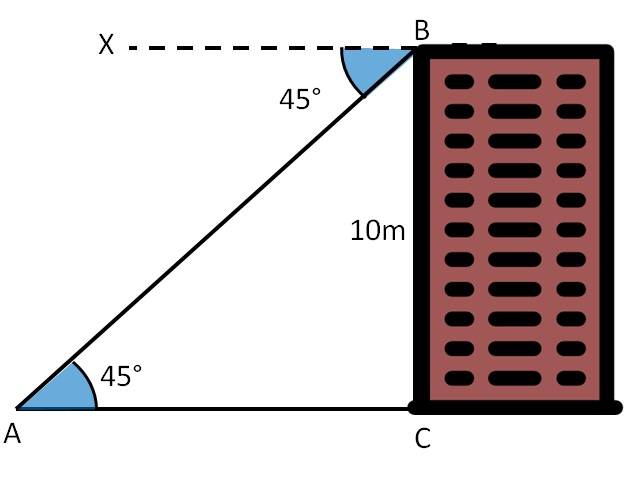
1706366538218

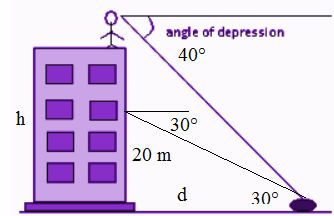
1706366539863

Frequently Asked Questions (FAQs)

1. What is an example of an angle of depression?

You could estimate the angle of depression, for instance, by standing on top of a hill or a structure and looking down at an object. A clinometer or a theodolite can be used to measure these angles

2. How to identify the angle of depression?

The angle of elevation is the angle between a person's horizontal line of sight and an item when they are standing and looking up at it. The angle of depression is the angle between the horizontal line of sight and the object when a person is standing and looking down at something.

3. Where does the angle of depression go?

The angle of depression is the angle formed by your line of sight and the horizontal (when looking down).

4. Why is it called the angle of depression?

If the line of sight is directed downward from the horizontal line, then an angle is created with the horizontal line. The angle produced between the horizontal line and the observer's line of sight is known as the angle of depression if the object being observed is below the observer's level.

5. Is the angle of depression always outside?

Always, the depression's angle is outside the triangle. It never falls within the triangle. From a horizontal line, it is at a downward angle. You might consider the angle of depression in terms of how your eyes move.

6. Can you have a negative angle of depression?

No, you cannot have a negative angle of depression. If the angle is measured upward from the horizontal, it becomes an angle of elevation, which is always positive.

7. How do you convert an angle of depression to an angle of elevation?

To convert an angle of depression to an angle of elevation, simply switch the positions of the observer and the object. The numerical value of the angle remains the same, but it changes from depression to elevation or vice versa.

8. Can the angle of depression be zero? If so, what does this mean?

Yes, the angle of depression can be zero. This occurs when the observer's line of sight is exactly horizontal, meaning they are at the same height as the object they're looking at.

9. Can two angles of depression from different heights to the same object be equal?

No, two angles of depression from different heights to the same object cannot be equal unless the observers are at the same height. The angle of depression changes with height if the horizontal distance remains constant.

10. What's the difference between the angle of depression and the angle the line of sight makes with the vertical?

The angle of depression is measured from the horizontal down to the line of sight. The angle the line of sight makes with the vertical is the complement of the angle of depression, meaning these two angles add up to 90 degrees.

11. In a right-angled triangle formed by an angle of depression, which side represents what?

In the right-angled triangle: the vertical side represents the height difference between the observer and the object, the horizontal side represents the distance between the observer and the object, and the hypotenuse represents the direct line of sight.

12. What's the relationship between the angle of depression and the distance to the object?

As the horizontal distance to the object increases (assuming a fixed height), the angle of depression decreases. Conversely, as the distance decreases, the angle of depression increases.

13. How does the angle of depression relate to the concept of slope in coordinate geometry?

The tangent of the angle of depression is equivalent to the absolute value of the slope of the line connecting the observer to the object. Both represent the ratio of vertical change to horizontal change.

14. How does the angle of depression feature in navigation and aviation?

In navigation and aviation, the angle of depression is crucial for determining distances and positions. Pilots use it to judge their approach to runways, and ships use it to estimate distances to landmarks or other vessels.

15. How does atmospheric refraction affect the measured angle of depression?

Atmospheric refraction can slightly alter the apparent angle of depression. Light bends as it passes through air layers of different densities, which can make distant objects appear slightly higher than they actually are, slightly decreasing the apparent angle of depression.

16. What is the angle of depression?

The angle of depression is the angle formed between the horizontal line of sight and the line of sight to an object below the observer. It is measured downward from the horizontal.

17. How does the angle of depression differ from the angle of elevation?

The angle of depression is measured downward from the horizontal, while the angle of elevation is measured upward from the horizontal. They are complementary angles, meaning they add up to 90 degrees.

18. Is there a formula for calculating the angle of depression?

There isn't a single formula for the angle of depression itself. However, we use trigonometric ratios (sine, cosine, tangent) to solve problems involving angles of depression, depending on the given information and what needs to be calculated.

19. How is the angle of depression related to the angle of elevation?

The angle of depression from point A to point B is equal to the angle of elevation from point B to point A. They form alternate angles when the line of sight intersects parallel lines (the horizontal lines at each point).

20. Can the angle of depression ever be greater than 90 degrees?

No, the angle of depression is always less than or equal to 90 degrees. If it were greater than 90 degrees, the line of sight would be pointing upwards, which would then be an angle of elevation.

21. In what real-life situations might we use the angle of depression?

Angle of depression is used in various real-life scenarios such as navigation, surveying, architecture, and military applications. For example, a person standing on a cliff looking down at a boat in the sea, or a pilot viewing the runway while landing an aircraft.

22. How does changing your height affect the angle of depression to a fixed object?

Increasing your height will increase the angle of depression to a fixed object, while decreasing your height will decrease the angle of depression. This is because the vertical component of the triangle formed increases or decreases, respectively.

23. How does the angle of depression change as you move closer to or farther from an object?

As you move closer to an object below you, the angle of depression increases. As you move farther away, the angle of depression decreases. This is because the ratio of height difference to horizontal distance changes.

24. Can two different positions have the same angle of depression to an object?

Yes, two different positions can have the same angle of depression to an object. This occurs when the ratio of height difference to horizontal distance remains constant, even if the actual heights and distances change.

25. What's the relationship between the tangent of the angle of depression and the height and distance?

The tangent of the angle of depression is equal to the ratio of the height difference between the observer and the object to the horizontal distance between them. Mathematically, tan(θ) = height / distance, where θ is the angle of depression.

26. How do you measure the angle of depression in real life?

In real life, the angle of depression can be measured using instruments like clinometers, theodolites, or even smartphone apps with built-in inclinometers. These tools measure the angle between the horizontal and the line of sight to the object below.

27. How do you solve a problem if you're given the angle of depression and the direct distance to an object?

If you're given the angle of depression and the direct distance (hypotenuse), you can use the sine and cosine functions to find the height difference and horizontal distance respectively. sin(θ) = opposite/hypotenuse for height, and cos(θ) = adjacent/hypotenuse for horizontal distance.

28. Can you use the angle of depression to find the height of a tall object?

Yes, you can use the angle of depression to find the height of a tall object if you know your own height and the horizontal distance to the object. By using the tangent function, you can calculate the height difference, then add your height to get the object's total height.

29. How does the angle of depression relate to the concept of parallax?

Parallax, the apparent change in position of an object when viewed from different points, is related to the angle of depression. The difference in angles of depression from two different observation points can be used to calculate the distance to an object, which is the principle behind parallax.

30. How might angle of depression be used in sports?

In sports, the angle of depression comes into play in activities like diving (angle of entry into water), ski jumping (angle of descent), or in ball sports when considering the trajectory of a ball thrown or hit from a height.

31. In coastal engineering, how might the angle of depression be utilized?

Coastal engineers might use the angle of depression when designing sea defenses, planning beach nourishment projects, or studying coastal erosion. It helps in understanding how waves approach the shore and how structures will interact with the water.

32. In the field of acoustics, how might the angle of depression be relevant?

In acoustics, the angle of depression can be important when considering how sound travels in open spaces or how to design sound systems for large venues. It can affect how sound is perceived at different locations and heights, which is crucial for creating even sound distribution in stadiums or amphitheaters.

33. How is the angle of depression used in trigonometry problems?

In trigonometry problems, the angle of depression is often used to set up right-angled triangles. The known angle and any given distances can then be used with trigonometric ratios (sine, cosine, tangent) to calculate unknown distances or heights.

34. What common mistake do students make when solving angle of depression problems?

A common mistake is confusing the angle of depression with the angle formed at the base of the imaginary right-angled triangle. Remember, the angle of depression is at the observer's eye level, not at the base of the triangle.

35. How do you determine which trigonometric ratio to use in an angle of depression problem?

The choice of trigonometric ratio depends on what information is given and what you need to find. If you know the adjacent and want the opposite, use tangent. If you know the hypotenuse and want the opposite, use sine. If you know the hypotenuse and want the adjacent, use cosine.

36. How does the concept of similar triangles relate to angle of depression problems?

Similar triangles are often used in angle of depression problems when there are multiple observers at different heights looking at the same object. The angles of depression form similar triangles, allowing us to set up proportions to solve for unknown values.

37. In a triangle formed by an angle of depression, which angle is always 90 degrees?

In a triangle formed by an angle of depression, the angle at the base of the triangle, where the vertical height line meets the horizontal distance line, is always 90 degrees.

38. How do you approach a problem where you need to find the angle of depression?

To find the angle of depression, you typically need the height difference and the horizontal distance. Once you have these, you can use the arctangent (tan^-1) function: θ = tan^-1(height difference / horizontal distance).

39. Can the angle of depression ever be exactly 90 degrees?

Theoretically, the angle of depression could be 90 degrees if you're looking straight down, but in practical situations, this is nearly impossible as you'd need to be directly above the object with no horizontal displacement.

40. How does the angle of depression relate to the field of view?

The angle of depression affects the lower limit of your field of view. A larger angle of depression means you can see more of what's below you, while a smaller angle means your view of lower areas is more limited.

41. In surveying, how is the angle of depression used?

In surveying, the angle of depression is used to calculate distances and heights of terrain features. Surveyors use instruments like theodolites to measure these angles accurately, which helps in creating topographic maps and planning construction projects.

42. How do you solve a problem involving two different angles of depression to the same object?

When you have two different angles of depression to the same object (from two different heights), you can set up a system of equations using the tangent function for each angle. This allows you to solve for both the horizontal distance and the height of the lower object.

43. What's the relationship between the angle of depression and the distance at which an object disappears over the horizon?

As an object moves farther away, the angle of depression decreases until it reaches zero when the object is at the horizon. The distance at which an object disappears over the horizon depends on the observer's height and the Earth's curvature.

44. How does the concept of angle of depression apply in satellite imagery or aerial photography?

In satellite imagery and aerial photography, the angle of depression affects the perspective and coverage of the images. A smaller angle of depression (closer to horizontal) covers a larger area but with less detail, while a larger angle provides more detailed images of a smaller area.

45. Can you use the angle of depression to estimate the speed of an object moving away from you?

Yes, by measuring the angle of depression at regular time intervals as an object moves away, you can calculate its speed. The change in angle over time, combined with known height, allows you to determine the object's horizontal speed using trigonometric calculations.

46. How does the angle of depression feature in architecture and building design?

Architects and designers use angles of depression to consider sightlines from buildings, ensure privacy, plan window placements, and design features like balconies or terraces. It's also important in planning how a building will appear from different vantage points.

47. What role does the angle of depression play in optics and camera design?

In optics and camera design, understanding angles of depression is crucial for determining field of view, especially for wide-angle lenses or when designing cameras for specific purposes like security or wildlife photography.

48. How is the angle of depression used in astronomy?

In astronomy, the angle of depression (more commonly referred to as the negative altitude) is used when observing celestial objects that are below the horizon. It's particularly useful in calculating rise and set times of celestial bodies.

49. Can you use the angle of depression to find the depth of a well or a valley?

Yes, if you know your height above the ground and the horizontal distance to the edge of the well or valley, you can use the angle of depression to calculate its depth. The tangent of the angle of depression multiplied by the horizontal distance gives the depth.

50. How does the Earth's curvature affect angle of depression calculations over very long distances?

For very long distances, the Earth's curvature becomes significant and can affect angle of depression calculations. The actual angle will be slightly larger than what would be calculated assuming a flat Earth, due to the curvature dropping the far point lower than a flat plane would.

51. In video game design, how might developers use the concept of angle of depression?

Game developers use angles of depression in designing camera angles, especially in third-person games. It's also used in creating realistic terrain and in programming AI for tasks like aiming or navigating 3D environments.

52. Can the angle of depression be used in meteorology?

Yes, in meteorology, the angle of depression can be used when observing weather phenomena. For example, it can help in estimating the distance to a storm by observing lightning, or in determining the height of cloud bases.

53. How does the angle of depression feature in the design of roller coasters?

Roller coaster designers use angles of depression (and elevation) to calculate the forces experienced by riders, ensure thrilling yet safe drops, and design the overall layout of the track. The angle of depression is crucial in creating the sensation of freefall in steep drops.

54. Can you use the angle of depression to estimate the height of clouds?

Yes, by measuring the angle of depression to the edge of a cloud's shadow on the ground, and knowing the distance to that shadow, you can calculate the height of the cloud using trigonometry.

55. How might angle of depression be used in virtual reality (VR) applications?

In VR, understanding and correctly representing angles of depression is crucial for creating realistic 3D environments. It affects how objects are perceived in the virtual space, especially when simulating views from heights or in applications like virtual architecture tours.