Annulus - Definition, Formula, Examples

Annulus

Edited By Team Careers360 | Updated on Jul 02, 2025 05:17 PM IST

An annulus is a shape made up of two circles. The inner region between two concentric circles, or two or more circles with the same centre point, is known as an annulus. A plane shape known as an annulus is created by two concentric circles. Both circles have a common centre. The annulus resembles a ring in shape. With a round hole in the centre, it is regarded as a circular disc. Examples of annular shapes in everyday objects include finger rings, doughnuts, CDs, etc.

This Story also Contains

What Is An Annulus?
What Does An Annulus Look Like?
Area Of Annulus
Perimeter Of Annulus

What Is An Annulus?

The annulus is the area enclosed between two concentric circles. Concentric circles are those that have the same centre. A circle is a plane shape composed of points that are placed at a uniform distance from a central point. If a circle is encircled by another circle with a radius larger than this circle, then the space or gap between them is the annulus.

What Does An Annulus Look Like?

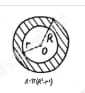
1706460017555

The annulus is shown in the above illustration by the shaded area.

The illustration above depicts two circles: an inner circle, which is a smaller circle, and an outer circle, which is a larger circle. Point O represents the centre of both the circles.

Area Of Annulus

By calculating the areas of the outer and inner circles, the area of the annulus may be computed. The result is then obtained by deducting the area of the inner circle from the area of the outer circle.

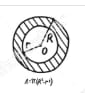
1706460017614

Two circles have the same centre, O, in the illustration above. Let the inner circle's radius be "r," and the outer circle's radius be "R." An annulus is indicated by the shaded area. We must determine the areas of the two circles in order to determine the area of this annulus.

Area of outer circle=\pi R^{2}

Area of inner circle=\pi r^{2}

The area of the annulus equals the difference between the inner and outer circles.

Area of annulus=\pi (R^{2}-r^{2})

This can also be written as, \pi (R+r)(R-r)

Perimeter Of Annulus

The perimeter of a two-dimensional shape is the total linear distance its boundaries cover. As a result, the annulus' perimeter will be equal to the sum of the distances travelled by its outer and inner circles.

If the inner circle's radius is r and the outer circle's radius is R, the annulus's perimeter will be:

2\pi R+2\pi r

This can also be written as, 2\pi (R+r)

Frequently Asked Questions (FAQs)

1. What is an an annulus?

The inner region between two concentric circles, or two or more circles with the same centre point, is known as an annulus.

2. Define concentric circles.

The circles with a common centre are known as concentric circles.

3. How is the area of the annulus calculated?

By calculating the areas of the outer and inner circles, the area of the annulus may be computed. The resultant area of the annulus is then obtained by deducting the area of inner circle from the area of the outer circle.

4. Give a few examples of annular shapes in real life.

Examples of annular shapes in everyday objects include finger rings, doughnuts, CDs, etc.

5. What is the formula for calculating the perimeter of the annulus?

The perimeter of the annulus is calculated as, 2\pi (R+r) .

Here, “R” is the radius of the outer circle and “r” is the radius of the inner circle.

6. How is the area of an annulus calculated?

The area of an annulus is calculated by subtracting the area of the smaller circle from the area of the larger circle. The formula is: A = π(R² - r²), where R is the radius of the larger circle and r is the radius of the smaller circle.

7. Can the area of an annulus ever be zero?

Theoretically, the area of an annulus approaches zero as the radii of the inner and outer circles become very close to each other. However, it can never be exactly zero unless the two circles are identical, at which point it's no longer an annulus.

8. How does changing the outer radius affect the area of an annulus?

Increasing the outer radius while keeping the inner radius constant will increase the area of the annulus. The relationship is quadratic, meaning the area increases proportionally to the square of the outer radius.

9. How does changing the inner radius affect the area of an annulus?

Increasing the inner radius while keeping the outer radius constant will decrease the area of the annulus. Again, this relationship is quadratic, with the area decreasing proportionally to the square of the inner radius.

10. Can an annulus have an area larger than the circle with the same outer radius?

No, an annulus cannot have an area larger than the circle with the same outer radius. The annulus is always a portion of this larger circle, so its area will always be smaller than or equal to the area of the full circle.

11. What's the relationship between the circumferences of the inner and outer circles of an annulus?

The difference between the circumferences of the outer and inner circles of an annulus is always 2π times the difference between their radii. This is because the circumference of a circle is 2πr, where r is the radius.

12. How is the perimeter of an annulus calculated?

The perimeter of an annulus is the sum of the circumferences of its inner and outer circles. It can be calculated using the formula: P = 2π(R + r), where R is the outer radius and r is the inner radius.

13. What's the significance of π in annulus calculations?

π (pi) is crucial in annulus calculations because it's fundamental to circular geometry. It appears in formulas for both area and perimeter of an annulus, reflecting the curved nature of the shape.

14. How do you find the width of an annulus?

The width of an annulus is the difference between the outer and inner radii. If R is the outer radius and r is the inner radius, the width is simply R - r.

15. Can an annulus have a negative area?

No, an annulus cannot have a negative area. Area is always a positive quantity or zero. If calculations result in a negative area, it likely means the inner and outer radii have been swapped or there's an error in the calculation.

16. What real-world objects resemble an annulus?

Many objects resemble an annulus, such as washers, rings, donuts, CD/DVD discs, some types of pools, and circular running tracks. Understanding annuli helps in designing and calculating dimensions for these objects.

17. Can the concept of an annulus be extended to three dimensions?

Yes, the 3D equivalent of an annulus is called a torus. It's essentially an annulus rotated around an axis, creating a donut-like shape. The principles of calculating surface area and volume become more complex in 3D.

18. How is the concept of an annulus used in real-world applications?

Annuli are used in various fields including engineering (for designing gears, washers), architecture (circular structures), physics (describing planetary orbits), and even in computer graphics for creating circular user interface elements.

19. Can you have a "negative" annulus?

There's no such thing as a "negative" annulus in geometry. An annulus is defined by its inner and outer radii, both of which must be positive. The concept of negativity doesn't apply to this shape.

20. What's the difference between an annulus and a washer in mathematics?

In mathematics, "annulus" and "washer" are often used interchangeably. Both refer to the region between two concentric circles. The term "washer" is sometimes preferred in calculus, especially when discussing the washer method for calculating volumes of revolution.

21. What is an annulus?

An annulus is a ring-shaped region formed between two concentric circles. It's the area enclosed by a larger circle with a smaller circle cut out from its center. The word "annulus" comes from Latin, meaning "little ring."

22. What's the difference between an annulus and a circle?

A circle is a single round shape, while an annulus is a ring-shaped region between two concentric circles. An annulus has both an outer and inner boundary, whereas a circle has only an outer boundary.

23. Can an annulus have equal inner and outer radii?

No, an annulus cannot have equal inner and outer radii. If the inner and outer radii were equal, there would be no area between the circles, and it would no longer be an annulus but simply a circle.

24. How does the concept of an annulus relate to concentric circles?

An annulus is directly related to concentric circles. It's the region between two concentric circles, where concentric circles are circles that share the same center point but have different radii.

25. How does the concept of an annulus relate to sectors and segments of a circle?

While sectors and segments are portions of a single circle, an annulus involves two circles. However, you can create an annular sector or segment by applying the concepts of sectors or segments to an annulus.

26. What happens to the area of an annulus if you double both the inner and outer radii?

If you double both the inner and outer radii, the area of the annulus will quadruple. This is because the area formula involves squaring the radii, so doubling each radius results in a factor of 4 increase in area.

27. What's the relationship between the area of an annulus and the areas of its constituent circles?

The area of an annulus is always equal to the difference between the areas of its outer and inner circles. Mathematically, this is expressed as: A_annulus = A_outer - A_inner = π(R² - r²).

28. How does the area of an annulus change as the difference between its inner and outer radii increases?

As the difference between the inner and outer radii increases (while keeping one radius constant), the area of the annulus increases. This increase is not linear but quadratic, as it depends on the square of the radii difference.

29. How would you find the inner radius of an annulus if you know its area and outer radius?

To find the inner radius r, given the area A and outer radius R, you would use the formula A = π(R² - r²) and solve for r. Rearranging the equation gives: r = √(R² - A/π).

30. What's the relationship between the area of an annulus and the area of a circle with a radius equal to the annulus's width?

There's no direct relationship between these areas. The area of an annulus depends on both its inner and outer radii, while the area of a circle depends only on its single radius. They will generally be different unless by coincidence.

31. How would you calculate the area of an annulus if given its outer circumference and width?

If given the outer circumference C and width w, you can calculate the area as follows:

32. How does the area of an annulus change if you increase both radii by the same amount?

If you increase both the inner and outer radii by the same amount, the area of the annulus will increase. The increase in area will be greater for annuli with larger original radii, due to the quadratic nature of the area formula.

33. Can you have an annulus with a hole that isn't circular?

In standard geometry, an annulus is defined as the region between two concentric circles. If the inner "hole" isn't circular, it wouldn't technically be an annulus. However, in some contexts, the term might be loosely applied to similar shapes with non-circular inner boundaries.

34. How is an annulus different from a ring in mathematical terms?

In mathematics, the terms "annulus" and "ring" are often used interchangeably when referring to the region between two concentric circles. However, "ring" has a broader meaning in abstract algebra, where it refers to a specific algebraic structure, unrelated to geometry.

35. What's the relationship between the area of an annulus and the area of a circle with a radius equal to the average of the annulus's inner and outer radii?

There's no simple, direct relationship. The area of the annulus will always be less than the area of this average circle. The difference depends on the specific inner and outer radii of the annulus.

36. How would you find the outer radius of an annulus if you know its area and inner radius?

To find the outer radius R, given the area A and inner radius r, use the formula A = π(R² - r²) and solve for R. Rearranging the equation gives: R = √(r² + A/π).

37. Can the area of an annulus be expressed in terms of its perimeter and width?

Yes, the area of an annulus can be expressed in terms of its perimeter P and width w. The formula is: A = (P/2)w - πw². This comes from expressing the radii in terms of P and w, and then substituting into the standard area formula.

38. How does the concept of an annulus relate to polar coordinates?

In polar coordinates, an annulus can be described as the region between two circles centered at the origin. It's defined by an inequality r₁ ≤ r ≤ r₂, where r is the radial coordinate, and r₁ and r₂ are the inner and outer radii respectively.

39. What's the difference between an annulus and an annular sector?

An annulus is the entire region between two concentric circles. An annular sector is only a portion of this region, bounded by two radial lines. It's like a "slice" of the annulus, similar to how a sector relates to a full circle.

40. How would you calculate the area of an annulus using integration?

Using polar coordinates, you can calculate the area of an annulus by integrating r dr dθ over the appropriate bounds. The integral would be: A = ∫₀²ᵖ ∫ᵣ¹ʳ² r dr dθ, where r₁ and r₂ are the inner and outer radii respectively.

41. Can you have a three-dimensional annulus?

Yes, a three-dimensional annulus is possible. It's called a hollow cylinder or cylindrical shell. It's the region between two coaxial cylinders, like a pipe. The volume is calculated similarly to the area of a 2D annulus, using the difference of the volumes of the outer and inner cylinders.

42. How does the concept of an annulus apply in probability theory?

In probability theory, particularly in two-dimensional continuous probability distributions, an annulus can represent a region of possible outcomes. The probability of an event occurring within this region would be calculated by integrating the probability density function over the annulus.

43. What's the relationship between an annulus and a circular crown in geometry?

"Annulus" and "circular crown" are synonymous terms in geometry. Both refer to the region between two concentric circles. The term "circular crown" is less commonly used but can be found in some mathematical texts.

44. How would you find the radii of an annulus if you know its area and perimeter?

Given the area A and perimeter P of an annulus, you can find the radii by solving a system of two equations:

45. Can the concept of an annulus be applied to ellipses?

Yes, the concept can be extended to ellipses. An elliptical annulus is the region between two concentric ellipses. The mathematics becomes more complex, as ellipses are described by two radii (semi-major and semi-minor axes) rather than one.

46. How does the area of an annulus compare to the area of a rectangle with the same perimeter and width?

The area of an annulus is always less than the area of a rectangle with the same perimeter and width. This is because the annulus "curves inward" while the rectangle has straight sides, resulting in less area for the annulus.

47. What's the relationship between the area of an annulus and the sum of the areas of its inner and outer circles?

The area of an annulus is always less than the sum of the areas of its inner and outer circles, but greater than the area of its outer circle alone. Specifically: A_outer < A_annulus < A_outer + A_inner.

48. How would you calculate the center of mass of a uniform annulus?

For a uniform annulus, the center of mass is located at its geometric center, which is the same as the center of both the inner and outer circles. This is due to the radial symmetry of the annulus.

49. Can you have an annulus on a sphere?

Yes, you can have an annulus on a sphere. It's called a spherical annulus or zone, and it's the region between two parallel planes intersecting a sphere. The area calculation is different from a planar annulus and involves the height of the zone and the radius of the sphere.

50. How does the concept of an annulus relate to the washer method in calculus?

The washer method in calculus uses the concept of an annulus to calculate volumes of solids of revolution. Each "slice" of the solid is treated as a thin annulus, and integrating these slices gives the total volume.

51. What's the relationship between the area of an annulus and the area of a circle with a diameter equal to the difference of the annulus's outer and inner diameters?

There's no simple, direct relationship. The area of this circle will always be less than the area of the annulus, but the exact relationship depends on the specific dimensions of the annulus.

52. How would you find the dimensions of an annulus with a given area and a specified ratio between its inner and outer radii?

If the area A is given and the ratio of inner to outer radius is r/R = k, you can solve this using the equation:

53. Can the concept of an annulus be applied in non-Euclidean geometry?

Yes, the concept of an annulus can be extended to non-Euclidean geometries like hyperbolic or spherical geometry. However, the properties and formulas for area and perimeter would be different from those in Euclidean geometry.

54. How does the moment of inertia of an annulus compare to that of a solid disc with the same outer radius?

The moment of inertia of an annulus is less than that of a solid disc with the same outer radius. This is because the annulus has less mass near its center, which contributes less to the moment of inertia. The exact relationship depends on the inner radius of the annulus.

55. What's the limit of the area of an annulus as its inner radius approaches its outer radius?

As the inner radius approaches the outer radius, the area of the annulus approaches zero. This is because the region between the two circles becomes infinitesimally thin, eventually disappearing when the radii are equal.