Area Between Two Curves in Calculus

Area bounded by curves and axis is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These integration concepts have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

Area Bounded by Curve and Axes

If the function $f(x) ≥ 0 ∀ x ∈ [a, b]$ then $\int_a^{\infty} f(x) d x$ represents the area bounded by $y = f(x), x-$axis and lines $x = a$ and $x = b$.

If the function $f(x) ≤ 0 ∀ x ∈ [a, b]$, then the area by bounded 4y = f(x), x-4axis and lines 4x = a$ and $x = b$ is $\int_a^b f(x) d x$.

Area along Y-axis

The area by bounded $x = g(y)$ [with $g(y)>0$], $y$-axis and the lines $y = a$ and $y = b$ is $\int_a^b x d y=\int_a^b g(y) d y$

Area of Piecewise Function

If the graph of the function $f(x)$ is of the following form, then

then $\int_a^b f(x) d x$ will equal $A_1-A_2+A_3-A_4$ and not $A_1+A_2+A_3+A_4$.

If we need to evaluate $A_1+A_2+A_3+A_1$ (the magnitude of the bounded area) we will have to calculate

$ \underbrace{\int_a^x f(x) d x}_{\mathrm{A}_1}+\underbrace{\left|\int_x^y f(x) d x\right|}_{\mathrm{A}_2}+\underbrace{\int_5^z f(x) d x}_{\mathrm{A}_3}+\underbrace{\left|\int_z^b f(x) d x\right|}_{\mathrm{A}_4} $

The area bounded by curve when curve intersects $X$-axis

The graph $y=f(x) \forall x \in[a, b]$ intersects $x-a x i s$ at $x=c$.

If the function $f(x) \geq 0 \forall x \in[a, c]$ and $f(x) \leq 0 \forall x \in[c, b]$ then area bounded by curve and $x$-axis, between lines $x=a$ and $x=b$ is

$ \int_a^b|f(x)| d x=\int_a^c f(x) d x-\int_c^b f(x) d x$

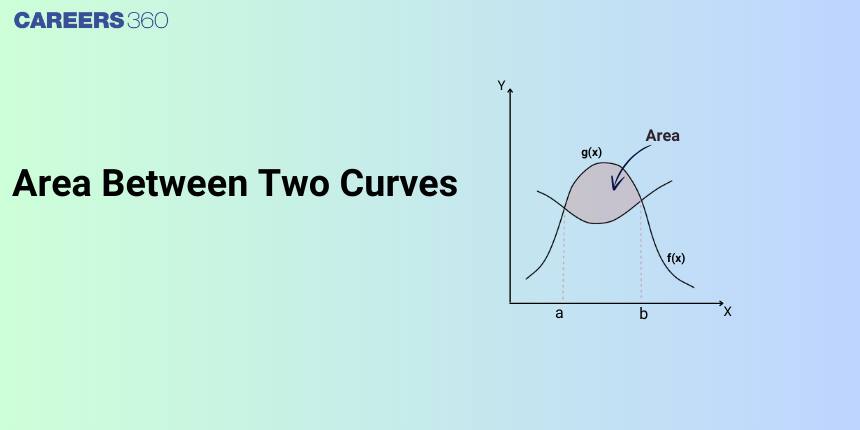
Area Bounded by Two Curves:

Area bounded by the curves $y=f(x), y=g(x) $ and the lines $ x = a$ and $x = b$, and it is given that $f(x) ≤ g(x). $

From the figure, it is clear that,

Area of the shaded region = Area of the region $ABEF$ - Area of the region $ABCD$

$\int_a^b g(x) d x-\int_a^b f(x) d x=\int_a^b(\underbrace{g(x)}_{\begin{array}{c}\text { upper } \\ \text { curve }\end{array}}-\underbrace{f(x)}_{\begin{array}{c}\text { lower } \\ \text { curve }\end{array}}) d x$

Area Bounded by Curves When Intersects at More Than One Point:

Area bounded by the curves $y = f(x), y = g(x)$ which intersect each other in the interval $[a, b]$

First find the point of intersection of these curves $y = f(x)$ and $y = g(x)$ by solving the equation $f(x) = g(x)$, let the point of intersection be $x = c $

Area of the shaded region

$=\int_a^c\{f(x)-g(x)\} d x+\int_c^b\{g(x)-f(x)\} d x$

When two curves intersects more than one point

Area bounded by the curves $y=f(x), y=g(x)$ which intersect each other at three points at $x = a, x = b$ and $x = c. $

To find the point of intersection, solve $f(x) = g(x). $

For $x ∈ (a, c), f(x) > g(x)$ and for $x ∈ (c, b),g(x) > f(x).$

Area bounded by curves,

$\begin{aligned} A & =\int_a^b|f(x)-g(x)| d x \\ & =\int_a^c(f(x)-g(x)) d x+\int^b(g(x)-f(x)) d x\end{aligned}$

Recommended Video Based on Area Between Two Curves

Solved Examples Based on Area Between Two Curves

Example 1: The area of the region (in sq. units) bounded by the curves $y=|x-1|$ and $y=3-|x|$ is
1) $4$
2) $3$
3) $6$
4) $2$

Solution:

The area between the curve $y=f(x), x$ axis and two ordinates at the point $x=a$ and $x=b(b>a)$ is given by $A=\int_a^b f(x) d x=\int_a^b y d x$

$ y=(x-1)$ and $y=3-(x)$

Example 2:The area of the region enclosed by the curves $y=x, x=e, y=1 / x$ and the positive $x$-axis is
1) $3 / 2$ square units
2) $5 / 2$ square units
3) $1 / 2$ square units
4) $1$ square units

Solution:

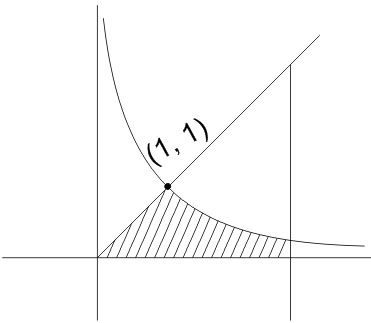
$\begin{aligned} & \int_0^1 x d x+\int_1^e \frac{1}{x} d x \\ & \Rightarrow\left[\frac{x^2}{2}\right]_0^1+[\log x]_1^e \\ & =\frac{1}{2}+\ln e \\ & =\frac{1}{2}+1=\frac{3}{2} \text { sq units }\end{aligned}$

Example 3:

The area bounded by the curves $y=\cos x$ and $y=\sin x$ between the ordinates $x=0$ and $x=\frac{3 \pi}{2}$ is
1) $
4 \sqrt{2}-2
$

2) $
4 \sqrt{2}+2
$

3) $
4 \sqrt{2}-1
$

4) $
4 \sqrt{2}+1
$

Solution

Area along $x$ axis -
Let $y_1=f_1(x)$ and $y_2=f_2(x)$ be two curve then area bounded between the curves and the lines $x=a$ and $x=b$ is

$
\left|\int_a^b \Delta y d x\right|=\left|\int_a^b\left(y_2-y_1\right) d x\right|
$

$\text { Where } \Delta y=f_2(x)-f_1(x)$

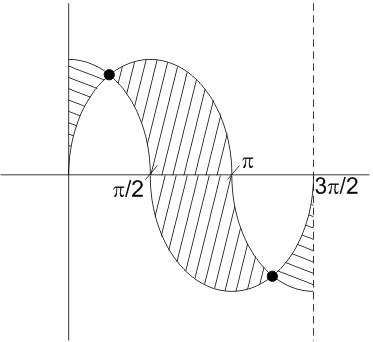
$\begin{aligned} & \text { Area }=\int_0^{\frac{\pi}{4}}(\cos x-\sin x) d x+\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}(\sin x-\cos x) d x+\int_{\frac{5 \pi}{4}}^{\frac{3 \pi}{2}}(\cos x-\sin x) d x \\ & =[\sin x+\cos x]_0^{\frac{\pi}{4}}+[-\cos -\sin x]_{\frac{5 \pi}{4}}^{\frac{5 \pi}{4}}+[\sin x+\cos x]_{\frac{5 \pi}{4}}^{\frac{3 \pi}{2}} \\ & =\sqrt{2}^{-1}+[\sqrt{2}+\sqrt{2}]+1(-1)+\sqrt{2} \\ & =4 \sqrt{2}-2\end{aligned}$

Example 4: The area (in sq. units) of the region described by $\mathrm{A}=\left\{(x, y) \mid y \geq x^2-5 x+4, x+y \geq 1, y \leq 0\right\}$ is :
1) $\frac{7}{2}$
2) $\frac{19}{6}$
3) $\frac{13}{6}$
4) $\frac{17}{6}$

Solution

Area along $x$ axis -
Let $y_1=f_1(x)$ and $y_2=f_2(x)$ be two curve then area bounded between the curves and the lines $x=a$ and $x=b$ is

$
\left|\int_a^b \Delta y d x\right|=\left|\int_a^b\left(y_2-y_1\right) d x\right|
$

$\text { Where } \Delta y=f_2(x)-f_1(x)$

Point of intersection of $y=x^2-5 x+4$ and $x+y=1$ are $x=1,3$ at $x=1, y=0$;

$
x=3, y=-2
$

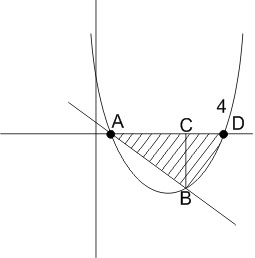
$\begin{aligned} & \text { Req Area }=\text { Area } \triangle A B C+\left|\int_3^4\left(x^2-5 x+4\right) d x\right| \\ & =\frac{1}{2} \times 2 \times 2+\left[\frac{x^3}{3}-\frac{5 x^2}{2}+4 x\right]_3^4 \\ & =\frac{19}{6}\end{aligned}$

Example 5: Area bounded (in sq. units) by the curves $4 y=\left|x^2-4\right|$ and $y+|x|=7$, is equal to
1) $32$
2) $16$
3) $4$
4) $8$

Solution

\begin{aligned}
&\text { If we have two functions intersection each other.First find the point of intersection. Then integrate to find area }\\
&\int_o^a[f(x)-9(x)] d x
\end{aligned}

$\begin{aligned} \text { Required area } & =2\left(\int_0^2\left(7-x-\left(\frac{4-x^2}{4}\right)\right) d x+\int_2^4\left(7-x-\left(\frac{x^2-4}{4}\right)\right) d x\right) \\ = & 2\left(\int_0^2\left(6-x-\frac{x^2}{4}\right) d x+\int_2^4\left(8-x-\frac{x^2}{4}\right) d x\right) \\ = & 2\left(6 x-\frac{x^2}{2}+\frac{x^3}{12}\right)_0^2+2\left(8 x-\frac{x^2}{2}-\frac{x^3}{12}\right)_2^4=32 \text { sq.units }\end{aligned}$