Area of Hexagon Formula - Explanation, Types, Solved Examples and FAQs
Area of hexagon formula
A hexagon is a polygon which has six sides and six angles. The word hexagon is derived from the Greek words “Hexa” and “gonia” which means “six” and “corner” respectively. There are two types of a hexagon:
This Story also Contains
- Table of contents
- Area of regular hexagon formula
- Area of regular hexagon using apothem
- Area of irregular hexagon
- Examples
Regular hexagon: All the sides and all the angles of a regular hexagon are of equal value. The order of rotational symmetry of a regular hexagon is six. It is composed of six equilateral triangles.
Irregular hexagon: All the sides and angles of an irregular hexagon are not the same.
The area of a hexagon is the space contained inside its sides. The area of a hexagon can be calculated in a number of different ways. The various techniques primarily depend on the way of splitting of the hexagon. We shall examine numerous approaches to calculating the area of a hexagon in this article.
Table of contents
Area of regular hexagon formula
Area of regular hexagon using apothem
Area of irregular hexagon
Examples
FAQs
Area of regular hexagon formula
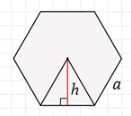
Area of a regular hexagon can be calculated by dividing the hexagon into six equilateral triangles. After dividing the hexagon into triangles, we compute the area of one equilateral triangle and multiply it by six to get the area of the hexagon.
Area of equilateral triangle is given by the following formula:
Area\: of \: equilateral\: triangle=\frac{\sqrt3}{4}a^2
![]()
Where, a is the length of the side of the equilateral triangle.
Since, the area of the hexagon is six times the area of the triangle we get the formula of area of hexagon as:
Area\: of\: hexagon=\frac{3\sqrt3}{2}a^2
![]()
Area of regular hexagon using apothem
Area of equilateral triangle using the height of the triangle is given by:
Area\: of \: equilateral\: triangle=\frac{1}{2}ah
![]()
Where, h is the height of the equilateral triangle and a is the base of the triangle.
Since, the area of the hexagon is six times the area of the triangle we get the formula of area of hexagon as:
Area\: of\: hexagon=3ah
![]()
The perimeter of a hexagon is equal to six times the side of the hexagon. Hence, the perimeter ‘p’ is equal to 6a.
Using the perimeter of the hexagon, the area of hexagon can be calculated by the following formula:
Area\: of\: hexagon=\frac{1}{2}ph
![]()
Area of irregular hexagon
There is no precise formula for determining the area of an irregular hexagon. The area of an irregular hexagon can be calculated by partitioning it into several shapes like squares, rectangles and triangles. The area of these shapes can be calculated individually and then summed up to determine the area of the hexagon.
Examples
Example 1: Find the area of a regular hexagon with side length equal to 5m.
Answer: Given, side of hexagon (a) = 5m.
Therefore,
Area\: of\: hexagon=\frac{3\sqrt3}{2}a^2\\
=\frac{3\sqrt3}{2}5^2m^2\\
=64.95m^2
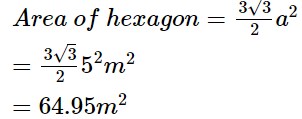
Example 2: If the length of side of a regular hexagon is equal to 4m and the length of apothem is equal to 3.464m then, find the area of the hexagon.
Answer: Given, the length of side (a) = 4m
The length of apothem (h) = 3.464m
The area of hexagon is given by:
Area\: of\: hexagon=3ah\\
=3 \times 4 \times 3.464 m^2\\
=41.568 m^2
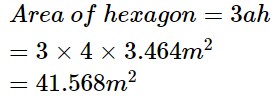
Example 3: Find the side of the regular hexagon whose area is equal to 260 sq. units.
Answer: Given area is equal to 260 sq. units.
Let the side of the hexagon be a. Then,
Area\: of\: hexagon = \frac{3\sqrt3}{2}a^2\\
\frac{3\sqrt3}{2}a^2 = 260\\
a= 10\: units
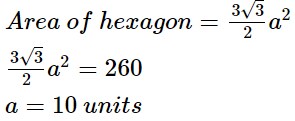
Frequently Asked Questions (FAQs)
The area of a regular hexagon is given by following formulas:
Area\: of\: hexagon=\frac{3\sqrt3}{2}a^2
Area\: of\: hexagon=3ah
Area\: of\: hexagon=\frac{1}{2}ph
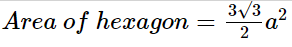
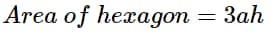
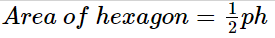
Here, ‘a’ is the side of the hexagon.
‘h’ is the length of the apothem of the hexagon.
‘p’ is the perimeter of the hexagon.
The perimeter of a hexagon is the sum of length of all six sides of a hexagon. If one side of a regular hexagon is equal to ‘a’ then its perimeter is equal to six times the side of the hexagon that is equal to ‘6a’.
A hexagon is a polygon with six sides and six angles.
A hexagon has two types: Regular hexagon and irregular hexagon.
If all the six sides and six angles of a hexagon are of equal value then the hexagon is regular hexagon otherwise, the hexagon is an irregular hexagon.
A polygon is a two-dimensional, closed geometrical shape that is flat or planar and is bordered by straight sides. Its sides are not curved or curled.