Area of Hexagon

Edited By Team Careers360 | Updated on Jan 20, 2025 03:43 PM IST

The portion or the region inside the six sides of the hexagon is called the area of the hexagon. A polygon can be defined as the closed 2-D shape with six sides and six angles. The Hexagon word comes from Greek words "Hexa," which means "six," and "Gona," which means "corner,".

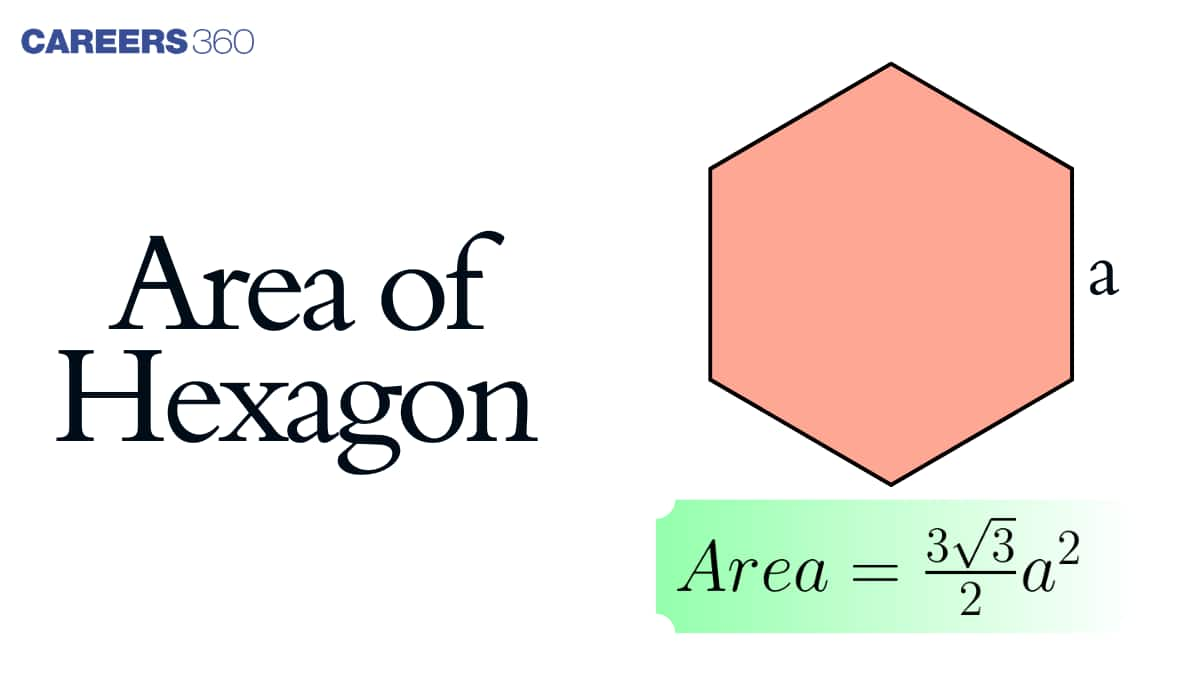
Hexagon

Hexagons are six-sided polygonal shapes. A hexagon is referred to as a regular hexagon if all of its sides are equal and all of its angles are the same. There are a total of 9 diagonals in a hexagon. A normal hexagon has 720 degrees total internal angles. The inner angles are all 120 degrees, as well. The outside angle of a regular hexagon is 60 degrees, while the total exterior angle is 360 degrees.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

Hexagon
Area Of Hexagon
Area Of Hexagon With Apothem

Area of Hexagon - Definition, Formula, Derivation and Examples

Six equilateral triangles make up a regular hexagon, which has six equal sides and six angles. Whether you're dealing with an irregular hexagon or a regular hexagon, there are numerous ways to figure out the area of a hexagon. The area of the hexagon formula can be calculated in a number of ways. There are several ways to compute a hexagon's area, which is stated in square units like $m^{2}, c m^{2}, i n^{2}, f t^{2}$ , and so on.

The area of a regular hexagon is calculated using the formula $\frac{3 \sqrt{3} a^{2}}{2}$ , where a is the length of a hexagonal side. The formula Area of the Hexagon = $\frac{3 \sqrt{3} a^{2}}{2}$ , which is the length of the hexagonal side, can be used to determine the area of a regular hexagon when one of its sides is known.

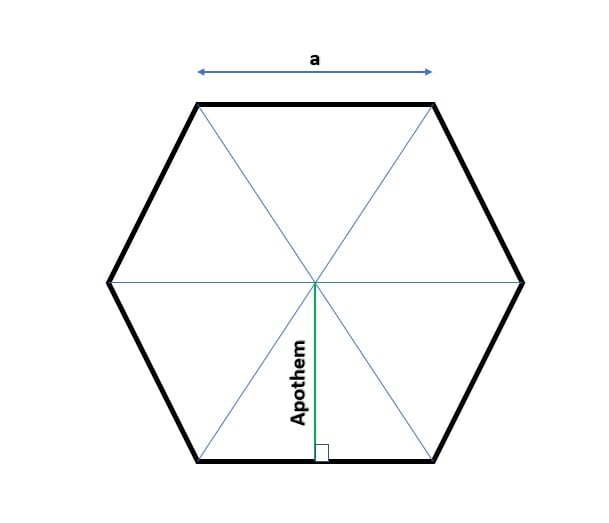
Area Of Hexagon With Apothem

When the side length and the apothem are known, the area of a regular hexagon can be determined. Apothem is the section of line traced from the hexagon's center that is parallel to each hexagonal side.

Area of hexagon = (1/2) × apothem × Perimeter of hexagon.

1706507423206

Frequently Asked Questions (FAQs)

1. What is the Area of Hexagon?

The area of the hexagon is defined as the area enclosed within the sides of the hexagon. The area of a hexagon is expressed in square units like $m^{2}, c m^{2}, i n^{2}, f t^{2}$ , and so on.

2. What will be the area of a regular hexagon if it has a side length of 8 units?

Given, the length of the side of the regular hexagon = 8 units.

We know that, The formula Area of the Hexagon = $\frac{3 \sqrt{3} s^{2}}{2}$ , here s is the side of the hexagon

Area of the Hexagon = $\frac{3 \sqrt{3} \times 8^{2}}{2} = 166.27$ sq. units

3. How Can We Find the Irregular Hexagon's Area?

The area of an asymmetric hexagon cannot be calculated using a precise formula. Triangles and rectangles can be used to partition a hexagon into multiple forms. The area of the hexagon can then be computed by adding the areas of these other forms.

4. What is the definition of Polygon?

A polygon is a straightforward closed curve. A polygon is a closed, two-dimensional shape that is circumscribed by three or more straight lines. Polygons include shapes like triangles, squares, rectangles, pentagons, and hexagons.

The sides of the polygon are the individual segments. Vertices are the places where two segments converge. Adjacent sides refer to segments that have the same vertex. A diagonal is a segment whose endpoints are non-adjacent vertices.