Area of Parallelogram Questions (with Solutions)

Edited By Team Careers360 | Updated on Jul 02, 2025 05:19 PM IST

2D or 3D shapes are the foundation of geometry. Each of these shapes has a unique set of features and uses a distinct area formula. The area of a parallelogram is the space it takes up on a two-dimensional plane. The area of a parallelogram is the region enclosed by its four sides. The area of a parallelogram is found by multiplying its length by its height.

This Story also Contains

What Is A Parallelogram?
What Is The Formula To Determine A Parallelogram's Area?
Perimeter Of Parallelogram
Types Of Parallelograms
Properties Of Parallelogram

What Is A Parallelogram?

A parallelogram is a four-sided, two-dimensional shape in geometry. It is a unique quadrilateral instance where the opposing sides are parallel and equal. The total of a quadrilateral's internal angles is 360 degrees. Two pairs of parallel sides with equal lengths make up a parallelogram. It has a perimeter and area because it is a two-dimensional figure. A parallelogram's interior opposite angles are also similar. A parallelogram has adjacent angles that sum to 180 degrees. Anything from a rectangle to a square to a rhombus can be a parallelogram.

What Is The Formula To Determine A Parallelogram's Area?

To find the parallelogram's area, multiply the perpendicular base by its height. In contrast to the lateral side of the parallelogram, which is not perpendicular to the base, the parallelogram's base and height are perpendicular to one another.

Therefore, the area of a parallelogram can be calculated using the formula below:

Area of parallelogram = Base * Height

If the length of adjacent sides and the angle between them are known, the area of a parallelogram can also be determined without knowing its height.

Area of parallelogram = ab\sin\theta 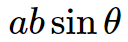1706509682965

Here, ‘a’ and ‘b’ represents the length of parallel sides and \theta 1706509682799 .

The length of a parallelogram's diagonals can also be used to determine its area. A parallelogram has two diagonals that cross one other at specific angles.

Area of parallelogram = \frac{1}{2}d_{1}d_{2}\sin x 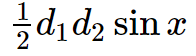1706509682453

Here, d_{1} 1706509682378 and d_{2} 1706509682700 represent the lengths of the two diagonals and ‘x’ represents the angle between the two diagonals.

Perimeter Of Parallelogram

Any shape's perimeter is either its entire length or the total distance enveloping it. In a similar manner, the total length of a parallelogram's edges determines its perimeter. Consequently, the following can be used to write the perimeter calculation formula:

Perimeter of parallelogram = 2(a+b)

Here, ‘a’ and ‘b’ represent the lengths of the sides of a parallelogram.

Types Of Parallelograms

There are three different types of parallelograms, as follows:

Rhombus - A parallelogram with equal sides is a rhombus. Every rhombus is a parallelogram because every pair of opposite sides is parallel.
Rectangle - A rectangle is a parallelogram when the diagonals are equal and all angles are right angles. Each interior angle of a rectangle, which is a particular instance of a parallelogram, is 90 degrees in measurement.
Square - A parallelogram with all equal sides and all 90-degree angles is called a square. The diagonals of a square are also equal.

Properties Of Parallelogram

The characteristics of a parallelogram are as follows:

Both sides will be congruent and parallel.
Congruence exists between the opposite angles.
The other angles are all right angles if any of the angles are right angles.
The two diagonals will cut each other in half.
The parallelogram is split into two congruent triangles by each diagonal.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Frequently Asked Questions (FAQs)

1. What is a parallelogram?

A parallelogram is a four-sided, two-dimensional shape in geometry. It is a unique quadrilateral instance where the opposing sides are parallel and equal.

2. Name the different types of parallelograms.

There are three different types of parallelograms, as follows:

Rhombus
Rectangle
Square

3. How to calculate the area of a parallelogram?

There are 3 methods to compute the area of a parallelogram:

When the parallelogram's height and base are known,

Area of parallelogram = Base * Height

When the length of adjacent sides and the angle between them are known,

Area of parallelogram = ab\sin\theta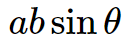

When the length of a parallelogram's diagonals and the angle between them is known,

Area of parallelogram = \frac{1}{2}d_{1}d_{2}\sin x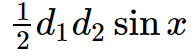

4. What is the perimeter of a parallelogram?

The total length of a parallelogram's edges determines its perimeter. The following formula can be used to compute the perimeter of a parallelogram:

Perimeter of parallelogram = 2(a+b)

Here, ‘a’ and ‘b’ represent the lengths of the sides of a parallelogram.

5. Define a rectangle.

A rectangle is a parallelogram when the diagonals are equal and all angles are at right angles. Each interior angle of a rectangle, which is a particular instance of a parallelogram, is 90 degrees in measurement.

6. Can you explain how the concept of work in physics relates to finding the area of a parallelogram?

The concept of work in physics (force × distance) is mathematically similar to finding the area of a parallelogram. In both cases, we're integrating a varying quantity (force or height) over a distance. This illustrates the broad applicability of integration in different fields.

7. How do you verify that your integrated result for a parallelogram's area is correct?

To verify, you can: 1) Check if the result matches the standard formula for simple cases, 2) Use graphing software to visualize and estimate the area, 3) Use numerical integration methods to approximate the result, or 4) Solve the problem using a different method and compare results.

8. Can you explain how parametric equations might be used in finding a parallelogram's area?

Parametric equations can be useful when the sides of the parallelogram are more easily expressed in parametric form. In this case, we'd typically convert the problem to a line integral around the boundary of the parallelogram, using Green's Theorem.

9. How do you handle a parallelogram problem where the height function involves trigonometric functions?

When the height function involves trigonometric functions, we often use trigonometric identities or u-substitution to simplify the integral. It's crucial to consider the period of these functions and how they relate to the limits of integration.

10. Can you explain how the concept of a vector cross product relates to finding a parallelogram's area?

The magnitude of the cross product of two vectors that define a parallelogram is equal to its area. This provides a quick way to calculate the area and connects the geometric concept of area to vector operations, bridging geometry and linear algebra.

11. How does changing the orientation of a parallelogram affect the integration process?

Changing the orientation can affect which axis we integrate with respect to. If the base is parallel to the y-axis instead of the x-axis, we might integrate with respect to y instead of x. The principle remains the same, but the setup of the integral changes.

12. Why do we need to use integration to find the area of some parallelograms?

Integration is necessary when dealing with parallelograms that have non-linear (curved) sides. In these cases, the height of the parallelogram varies along its base, making the standard formula inadequate. Integration allows us to account for this varying height.

13. What are some common mistakes students make when setting up integrals for parallelogram areas?

Common mistakes include: incorrectly identifying the height function, using the wrong limits of integration, forgetting to account for the angle of the parallelogram's sides, and not recognizing when to use integration (i.e., for curved-side parallelograms).

14. What is the basic principle behind using integration to find the area of a parallelogram?

The basic principle is to view the parallelogram as a continuous sum of thin rectangular strips. By integrating the height of these strips over the base of the parallelogram, we can calculate its area. This method allows us to handle parallelograms with non-linear sides as well.

15. How does the concept of definite integrals relate to finding the area of a parallelogram?

A definite integral represents the area under a curve between two points. When finding the area of a parallelogram, we're essentially calculating the area under the height function curve, which represents the parallelogram's shape.

16. What's the relationship between the area of a parallelogram and the area between two curves?

Finding the area of a parallelogram with curved sides is mathematically equivalent to finding the area between two curves. The top and bottom sides of the parallelogram can be thought of as two functions, and we're calculating the area between them.

17. How does the method for finding a parallelogram's area relate to finding the area of other shapes?

The method of integration for parallelograms is a specific application of a more general principle: finding areas by integrating. This same principle applies to finding areas of circles, ellipses, and arbitrary shapes bounded by functions. It's a foundational concept in calculus.

18. How do you approach a problem where the parallelogram is rotated at an angle to the coordinate axes?

When a parallelogram is rotated, we might need to use a coordinate transformation. This could involve rotating the coordinate system or using trigonometric functions to express the height in terms of the original coordinates before integrating.

19. How do you approach a problem where the parallelogram's height function is given implicitly?

When the height function is implicit, we may need to solve for y in terms of x first. If this isn't possible, we might need to use implicit differentiation or change the variable of integration. The key is to express the height as a function of the base variable before integrating.

20. How does the method for finding a parallelogram's area extend to finding the volume of a parallelepiped?

To find the volume of a parallelepiped, we extend the 2D integration to 3D. Instead of integrating the height function over a line (the base), we integrate the cross-sectional area function over a plane. This results in a double integral for volume.

21. What's the relationship between the area of a parallelogram and the absolute value of a determinant?

For a parallelogram defined by two vectors a and b, its area is equal to the absolute value of the determinant of the matrix formed by these vectors. This connects the geometric concept of area to the algebraic operation of finding determinants.

22. Can the area of a parallelogram ever be negative when using integration?

Mathematically, a negative area could result if we integrate from right to left (b < a) or if the height function is negative. However, in practical terms, area is always positive. A negative result usually indicates an error in setup or interpretation.

23. What role does the Fundamental Theorem of Calculus play in finding parallelogram areas?

The Fundamental Theorem of Calculus allows us to evaluate the definite integral that represents the parallelogram's area. It connects the concept of integration (summing infinitesimal areas) to anti-differentiation, providing a practical way to compute the result.

24. Can you use integration to find the area of a parallelogram in three-dimensional space?

Yes, but it requires multiple integrals. We'd typically use a double integral to account for both dimensions of the parallelogram in 3D space. This extends the concept from finding area to finding the surface area of a parallelogram in 3D.

25. What's the significance of the Mean Value Theorem in the context of parallelogram areas?

The Mean Value Theorem guarantees that for a continuous height function, there exists a point where the instantaneous height equals the average height. This helps us understand that the integrated area can be thought of as the product of the base length and an average height.

26. How do you set up the integral to find the area of a parallelogram?

To set up the integral, we first identify the base of the parallelogram along the x-axis, from a to b. Then, we determine the height function h(x). The area is given by the definite integral of h(x) from a to b: Area = ∫[a to b] h(x) dx.

27. How does the formula for the area of a parallelogram using integration differ from the standard formula?

The standard formula (base × height) works for parallelograms with straight sides. The integration method allows us to find the area of parallelograms with curved sides by integrating the varying height function over the base. This makes it more versatile for complex shapes.

28. What's the significance of the limits of integration in parallelogram area problems?

The limits of integration represent the start and end points of the parallelogram's base on the x-axis. They define the region over which we're summing the areas of infinitesimal strips to get the total area of the parallelogram.

29. How do you handle a parallelogram where both top and bottom sides are curves?

When both top and bottom sides are curves, we need to find two functions: one for the top curve f(x) and one for the bottom curve g(x). The height function becomes h(x) = f(x) - g(x), and we integrate this over the base: Area = ∫[a to b] [f(x) - g(x)] dx.

30. Can you explain the concept of a "height function" in the context of parallelogram area?

The height function h(x) represents how the height of the parallelogram changes as we move along its base. It's crucial for integration because it describes the shape of the parallelogram's sides. We integrate this function to find the total area.

31. How does the concept of a Riemann sum relate to finding a parallelogram's area through integration?

A Riemann sum approximates the area by dividing it into rectangles. As the number of rectangles approaches infinity, the Riemann sum approaches the true area. This is exactly what integration does, making the connection between discrete approximation and continuous summation.

32. How do you approach a problem where the parallelogram's area needs to be expressed as a function of a parameter?

To express the area as a function of a parameter, we integrate the height function symbolically, leaving the parameter as a variable. This results in an area function that can be analyzed for various values of the parameter, connecting integration to function analysis.

33. How do you handle a parallelogram problem where the height function is given as an infinite series?

When the height function is an infinite series, we integrate term by term, assuming the series converges uniformly. The result is another infinite series representing the area. This connects the concept of series to integration and requires careful consideration of convergence.

34. Can you explain how the concept of a Green's function might be used in finding a parallelogram's area?

While Green's functions are more commonly used in differential equations, they can be related to area problems. For instance, if the height function satisfies a differential equation, a Green's function approach might be used to solve for it before integration.

35. What's the significance of the Lebesgue integral in the context of parallelogram areas?

While the Riemann integral is usually sufficient for parallelogram areas, the Lebesgue integral provides a more general framework. It allows for integration of a broader class of functions, which can be relevant for parallelograms with very irregular height functions.

36. How do you approach a problem where the parallelogram's height function is only known at discrete points?

When the height function is only known at discrete points, we can use numerical integration techniques like the trapezoidal rule or Simpson's rule. This connects the continuous concept of area to discrete approximation methods, bridging calculus and numerical analysis.

37. How do you handle a parallelogram problem where the height function has discontinuities?

If the height function has discontinuities, we need to split the integral at these points. We integrate each continuous piece separately and then sum the results. This approach is based on the additive property of definite integrals.

38. What's the significance of the order of integration when dealing with parallelograms in multiple integrals?

The order of integration can affect the complexity of the problem. Sometimes, changing the order can simplify the integrand or the limits of integration. This is particularly important when dealing with parallelograms as regions of integration in double or triple integrals.

39. How does the method for finding a parallelogram's area relate to the concept of a line integral?

Finding a parallelogram's area can be formulated as a line integral around its boundary. This connection illustrates how different branches of calculus (integral calculus and vector calculus) can be used to solve the same problem, offering different insights.

40. What's the significance of the Jacobian determinant in the context of parallelogram areas?

The Jacobian determinant appears when we change variables in multiple integrals. For parallelograms, it's particularly relevant when we transform the region of integration. The absolute value of the Jacobian represents the factor by which areas are scaled during the transformation.

41. How do you approach a problem where the parallelogram's area needs to be maximized or minimized?

To maximize or minimize a parallelogram's area, we typically use optimization techniques from calculus. This involves expressing the area as a function of variable parameters, then finding the critical points using derivatives. It connects area calculation to optimization problems.

42. Can you explain how the concept of a flux integral relates to finding a parallelogram's area?

A flux integral measures the flow of a vector field through a surface. For a parallelogram, if we consider a constant unit vector field perpendicular to its plane, the flux through the parallelogram equals its area. This connects the geometric concept of area to vector calculus.

43. How does the method for finding a parallelogram's area extend to finding the area of a general quadrilateral?

For a general quadrilateral, we can split it into two triangles or treat it as a parallelogram with a varying height function. The integration process becomes more complex, often requiring piecewise functions or multiple integrals, but the fundamental principle remains the same.

44. What's the significance of the Divergence Theorem in the context of parallelogram areas?

While the Divergence Theorem is typically used for 3D volumes, it can be applied to 2D areas like parallelograms using a 2D version (Green's Theorem). This connects the area integral to a line integral around the boundary, offering an alternative method for area calculation.

45. How do you handle a parallelogram problem where the height function is defined piecewise?

For a piecewise height function, we split the integral at the points where the function definition changes. We integrate each piece separately using the appropriate function definition, then sum the results. This approach is based on the additive property of definite integrals.

46. Can you explain how the concept of a moment of inertia relates to finding a parallelogram's area?

The moment of inertia involves integrating the product of mass and distance squared. While not directly related to area, the integration process is similar. Understanding parallelogram areas helps in calculating moments of inertia for parallelogram-shaped plates in physics problems.

47. How does the method for finding a parallelogram's area relate to the concept of a surface integral?

Finding a parallelogram's area is a simple case of a surface integral. In higher dimensions, surface integrals extend this idea to curved surfaces. The parallelogram case helps build intuition for these more complex scenarios in vector calculus.

48. What's the significance of the Cauchy-Schwarz inequality in the context of parallelogram areas?

The Cauchy-Schwarz inequality provides an upper bound for the area of a parallelogram in terms of the lengths of its sides. This connects the geometric concept of area to algebraic inequalities, bridging geometry and analysis.

49. Can you explain how the concept of a Fourier series might relate to finding a parallelogram's area?

While not typically used for simple parallelograms, Fourier series can be relevant for parallelograms with periodic, complex height functions. The height function could be expressed as a Fourier series, and the area found by integrating this series term by term.

50. How does the method for finding a parallelogram's area extend to finding the area of a parallelogram on a curved surface?

For a parallelogram on a curved surface, we need to use techniques from differential geometry. The area involves integrating the magnitude of the cross product of tangent vectors over the parallelogram's parameter space, connecting flat geometry to curved space geometry.

51. What's the significance of the Fundamental Lemma of Calculus of Variations in the context of parallelogram areas?

The Fundamental Lemma of Calculus of Variations is crucial when we're trying to find a height function that maximizes or minimizes the parallelogram's area subject to certain constraints. It connects area optimization problems to the calculus of variations.

52. How does the method for finding a parallelogram's area relate to the concept of a probability density function?

The process of integrating a height function to find area is mathematically similar to integrating a probability density function to find probability. This connection illustrates how integration techniques apply across different fields, from geometry to probability theory.

53. Can you explain how the concept of a conformal mapping might relate to finding a parallelogram's area?

Conformal mappings preserve angles but not necessarily areas. If we conformally map a parallelogram to another shape, we need to account for the scaling factor (given by the absolute value of the derivative of the mapping function) when calculating the area.

54. How does the method for finding a parallelogram's area extend to finding the area of a parallelogram in non-Euclidean geometry?

In non-Euclidean geometry (like on a sphere or in hyperbolic space), the concept of a parallelogram and its area becomes more complex. We need to use the appropriate metric for the space and may need to employ techniques from differential geometry to set up and evaluate the integral.