Area Of Polygon - Definition & Finding Area of N Sided Polygons

The surface that a polygon occupies is known as its area. There are both regular and irregular polygons. The fundamental polygons used in geometry include triangles, squares, rectangles, pentagons, and hexagons, among others. Each of these polygons has a different area. All measurements are taken in square units, which are the standard measuring unit.

What Is A Polygon?

In mathematics, a polygon is a structure made of adjacent straight lines and is a part of geometry. Several straight lines come together to create a polygonal chain or circuit. Another way to describe it is as a rigid plane that is connected by two or more circuits. There are both regular and irregular polygons.

Types Of Polygons

A polygon can be categorised as regular or irregular based on the length of its sides.

• Regular polygon - Any polygon with equal sides and angles is said to be regular.

• Irregular polygon - A closed plane shape with unequal sides and angles is known as an irregular polygon.

How To Find A Regular Polygon’s Area?

If the number of sides of a regular polygon is known, one may use the formula to calculate its area,

Area of polygon is computed as: (Length of one side * Number of sides * Apothem)/2

Here, the apothem's length is indicated as:

Length of apothem = \frac{l}{2tan(\frac{180}{n})}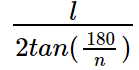

Here, the regular polygon has a side length of “l” and a number of sides, “n”.

The area of a regular polygon is expressed in terms of its perimeter as follows:

Area of polygon = (Perimeter * apothem)/2, where the perimeter of the polygon = Number of sides * Length of one side.

How To Determine An Irregular Polygon’s Area?

We divide an irregular polygon into a collection of regular polygons whose areas can be calculated using existing methods. This allows us to determine the area of irregular polygons.

Formulas For Calculating Area Of Few Polygons

• Triangle - \frac{1}{2}\times base\times height

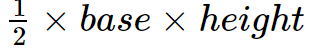
Heron's formula can be used to determine a triangle's area if we know the length of its sides, that is, Area = \sqrt{s(s-a)(s-b)(s-c)}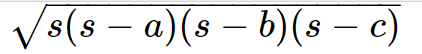

• Square - (side)^{2}

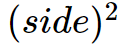
• Rectangle - Length x Breadth

• Pentagon - 5/2 × side length × distance from the center of sides to the center of pentagon

• Rhombus - 1/2 × product of diagonals

• Hexagon - (3√3)/2 × distance from center of sides to the center of hexagon

• Parallelogram - Base * Height

• Trapezium - (1/2) × (sum of lengths of its parallel sides or bases) × height

Points To Remember

• Finding an apothem allows one to determine the area of a regular polygon given the length of one side.

• Apothem divides a side into two equal portions by falling on its midway at a right angle.

• While a square has four sides, an equilateral triangle has three, making it a regular polygon. They are therefore not prefixed as regular before the form name.