Area of Regular Polygon - Definition, Formula and Examples
The space enclosed by a regular polygon's margin would be its area. In other terms, the region that a regular polygon encloses is its area. Typically, it is expressed in square units. Depending on the type of polygon—regular or irregular—different formulas can be used to calculate the area of the polygon.
This Story also Contains
- What Is A Polygon?
- The Formula For Calculating A Regular Polygon's Surface Area
- The Area Of A Regular Polygon With N Sides Formula
- A Regular Polygon's Area Inside A Circle
- Properties Of Polygon
What Is A Polygon?
A closed, two-dimensional shape composed of straight lines is known as a polygon in geometry. Each side must bisect exactly two other sides, but only at their ends. Polygons must have a common endpoint and noncollinear sides. We are aware that a triangle is a polygon with the least sides. Basically, the polygon can be categorized as either convex or concave and regular or irregular. Any polygon with equal sides and interior angles is said to be regular. The method used to determine the area of regular polygons is based on the corresponding formulas for each polygon. Remember that an n-gon is a polygon with n sides.
The Formula For Calculating A Regular Polygon's Surface Area
For some of the most popular polygons, the formulas for the area of regular polygons are as follows:
Area of an equilateral triangle = \frac{\sqrt{3}}{4}a^{2}
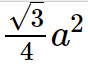
Here "a" denotes the triangle's equilateral triangle's side length.
Area of a Square = a^{2}
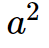
Here "a" denotes the square's side length.
Regular Pentagon’s Area = \frac{1}{4}\sqrt{[5(5+2\sqrt{5}]}a^{2}
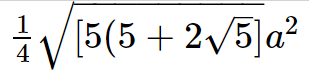
Here "a" is the pentagon's side length.
Regular Hexagon’s Area = \frac{3\sqrt{3}}{2}a^{2}
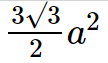
Here "a" denotes the hexagon's side length.
The Area Of A Regular Polygon With N Sides Formula
When a polygon has "n" sides, the following formula can be used to determine its area:
The formula for Area of Regular Polygons = \frac{l^{2}n}{4\tan\frac{180}{n}} 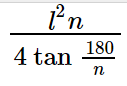
Here "l" denotes the polygon's side length.
A Regular Polygon's Area Inside A Circle
According to the following formula, the area of a regular polygon encircled by a circle is:
Area of a regular polygon encircled by a circle = \frac{nr^{2}}{2}\sin\frac{2\pi}{n} ![]()
Here "n" denotes the number of sides and “r” denotes the circumradius.
Properties Of Polygon
Finding an apothem allows one to determine the area of a regular polygon given the length of one side.
Apothem divides a side into two equal portions by falling at a right angle on its center.
A square is a regular polygon with four sides, whereas an equilateral triangle has three sides. They are not prefixed as regular before the form name as a result.
The total interior angle of an n-sided polygon is (n-2)\times180^{o}
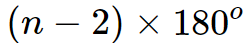
An n-sided regular polygon's inner angles are measured in terms of angles as: (n-2)\times\frac{180}{n}
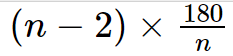
Each exterior angle of an n-sided regular polygon's angle measures \frac{360^{o}}{n}
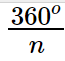
The number of diagonals in an n-sided polygon = \frac{n(n-3)}{2}
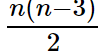
The number of triangles generated when a polygon's diagonals are connected from one corner = n-2
Frequently Asked Questions (FAQs)
The number of diagonals in an n-sided polygon = \frac{n(n-3)}{2} 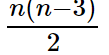
According to the following formula, the area of a regular polygon encircled by a circle is:
Area of a regular polygon encircled by a circle = \frac{nr^{2}}{2}\sin\frac{2\pi}{n} ![]()
Here "n" denotes the number of sides and “r” denotes the circumradius.
When a polygon has "n" sides, the following formula can be used to determine its area:
The formula for Area of Regular Polygons = \frac{l^{2}n}{4\tan\frac{180}{n}} 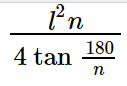
Here "l" denotes the polygon's side length.
Regular Pentagon’s Area = \frac{1}{4}\sqrt{[5(5+2\sqrt{5}]}a^{2} ![]()
Here "a" is the pentagon's side length.
Regular Hexagon’s Area = \frac{3\sqrt{3}}{2}a^{2} ![]()
Here "a" denotes the hexagon's side length.
Any polygon with equal sides and interior angles is said to be regular. Examples of regular polygons: Equilateral Triangles, squares, regular pentagons, and regular hexagons.