How to Find Area of Triangle: Formulas and Examples

In the realm of geometry, the triangle plays a very important part. So, finding the different properties of the triangle is essential. The area of a triangle is the region enclosed by the three sides of the triangle. In real life, we use the area of triangles in traffic signals, truss bridges, and pyramids.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is the Area of the Triangle?
2. Area of Triangle Formula
3. Area of an Equilateral Triangle
4. Area of an Isosceles Triangle
5. Area of a Triangle Given Two Sides and the Included Angle (SAS)
6. Solved Examples Based on the Area of Triangle

In this article, we will cover the concept of the area of a triangle. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept, including one in 2021.

What is the Area of the Triangle?

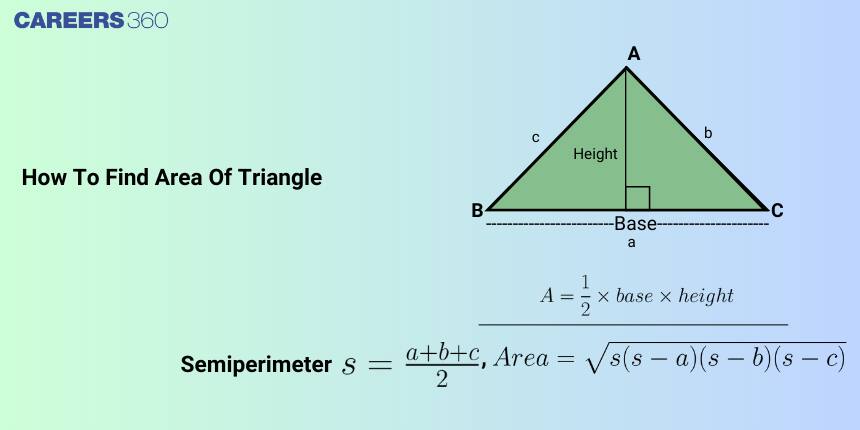
The area of a triangle is the region enclosed by the three sides of the triangle. There are many methods by which we can find the area of a triangle such as if the base and height of the triangle are given or three sides of a triangle are given or two sides and an angle enclosed between them is given.

The area of a triangle is usually denoted by $\Delta$ or $S$. There are many different formulas to find the area of the triangle.

Area of Triangle Formula

The area formula for a triangle is given as

Area = $½bh$, where ‘$b$’ is the base and ‘$h$’ is the height

Area of an Equilateral Triangle

An equilateral triangle is a triangle where all the sides are equal. The perpendicular drawn from the vertex of the triangle to the base divides the base into two equal parts.

Area of an Equilateral Triangle $=A=$ $(\surd 3)/4\times$ $sid{e}^2$

Area of an Isosceles Triangle

An isosceles triangle has two of its sides equal and also the angles opposite the equal sides are equal.

Area of an Isosceles Triangle = $1/2[\sqrt{}(a^2-b^2/4)\times b]$

Area of Triangle with Three Sides (Heron’s Formula)

The area of a triangle with $3$ sides of different measures can be calculated using Heron’s formula.

Consider a triangle $ABC$ then its area is given by

Area of triangle $=\sqrt{s}(s-a)(s-b)(s-c)$, where $s$ is semi-perimeter of a triangle given by $2\mathrm{s}=\mathrm{a}+\mathrm{b}+\mathrm{c}$

$\mathrm{\Delta }=\frac{1}{2}b\cdot \mathrm{c}\sin \mathrm{A}=\frac{1}{2}bc\cdot 2\sin \frac{\mathrm{A}}{2}\cos \frac{\mathrm{A}}{2}$

use half angle formula

$\begin{array}{rl}& =\frac{1}{2}\cdot bc\cdot \sqrt{\frac{(s-b)(s-c)}{bc}}\sqrt{\frac{s(s-a)}{bc}}\\ & =\sqrt{s(s-a)(s-b)(s-c)}\end{array}$

Area of a Triangle Given Two Sides and the Included Angle (SAS)

Clearly, height $h=c.sin(A)$

Area $=\frac{1}{2}$ (base $x$ height $)$
Area $=\frac{1}{2}(BC\times AD)$
Area $=\frac{1}{2}a\cdot c\cdot \sin A$
So area of a triangle is given by
Area $=\frac{1}{2}\mathrm{ac}\sin \mathrm{A}$
The area of triangle $ABC$ is represented by $\mathrm{\Delta }$,
Thus Area of the triangle is given by

$\text{ Area of }\begin{array}{rl}\mathrm{\Delta }\mathrm{ABC}=\mathrm{\Delta }& =\frac{1}{2}b\cdot \mathrm{c}\sin \mathrm{A}\\ & =\frac{1}{2}a\cdot \mathrm{b}\sin \mathrm{C}\\ & =\frac{1}{2}c\cdot \mathrm{a}\sin \mathrm{B}\end{array}$
adius of a triangle inscribed in a triangle,

The area of a triangle is given by
$\text{ Area }=\mathrm{\Delta }=\text{ r.s }$
where $s$ is the semi-perimeter of a triangle given by $2s=a+b+c$

Recommended Video Based on Area of Triangle:

Solved Examples Based on the Area of Triangle

Example 1: If in a triangle $\mathrm{ABC},AB=5$ units, $\mathrm{\angle }\mathrm{B}={\cos }^{-1}\left(\frac{3}{5}\right)$ and the radius of the circumcircle of $\mathrm{△}ABC$ is $5$ units, then the area (in sq. units) of $\mathrm{△}ABC$ is [JEE MAINS 2021]

Solution

Given, $AB=c=5,R=5$

$B={\cos }^{-1}\left(\frac{3}{5}\right)\Rightarrow \cos B=\frac{3}{5}\Rightarrow \sin B=\frac{4}{5}$

We know,

$\frac{b}{\sin B}=2R\Rightarrow b=2R\sin B=2\cdot 5\cdot \frac{4}{5}=8$

Using cosine rule.

$\begin{array}{rl}& \cos B=\frac{a^2+c^2-b^2}{2ac}\\ & \frac{3}{5}=\frac{a^2+25-64}{2\cdot a\cdot 5}\\ & \Rightarrow a^2-6a-39=0\\ & \Rightarrow a=\frac{6+8\sqrt{3}}{2}=3+4\sqrt{3}.\end{array}$

Now Area

$=6+8\sqrt{3}$

Hence, the correct answer is $6+8\sqrt{3}$

Example 2: In triangle $\mathrm{ABC}$ ratio of sides $a:b:c=3:4:5$ and it has an incircle which has a center at $\mathrm{O}$ then find the ratio of the area of $\mathrm{△}AOB:\mathrm{△}BOC:\mathrm{△}COA$

Solution

The area formula for a triangle is given as Area $=1/2$ bh, where ' $b$ ' is base and ' $h$ ' is the height. For oblique triangles, we must find ' $h$ ' before we can use the area formula.

$\begin{array}{rl}\text{ Area }& =\frac{1}{2}\text{ base }\times \text{ height }\\ & =\frac{1}{2}b\cdot c\sin \mathrm{A}\end{array}$

Area of triangle $ABC$ is represented by $\mathrm{\Delta }$, Thus

$\text{ Area of }\begin{array}{rl}\mathrm{△}\mathrm{ABC}=\mathrm{\Delta }& =\frac{1}{2}b\cdot \mathrm{c}\sin \mathrm{A}\\ & =\frac{1}{2}a\cdot \mathrm{b}\sin \mathrm{C}\\ & =\frac{1}{2}c\cdot \mathrm{a}\sin \mathrm{B}\end{array}$

NOTE:
Area of the triangle in terms of sides (heron's Formula)

$\mathrm{\Delta }=\frac{1}{2}b\cdot \mathrm{c}\sin \mathrm{A}=\frac{1}{2}bc\cdot 2\sin \frac{\mathrm{A}}{2}\cos \frac{\mathrm{A}}{2}$

use half angle formula

$\begin{array}{rl}& =\frac{1}{2}\sqrt{\frac{(s-b)(s-c)}{bc}}\sqrt{\frac{s(s-a)}{bc}}\\ & =\sqrt{s(s-a)(s-b)(s-c)}\end{array}$

From the above Diagram, we can see

$\begin{array}{rl}& \mathrm{\Delta }AOB:\mathrm{△}BOC:\mathrm{△}COA=\frac{1}{2}\times 3k\times r:\frac{1}{2}\times 4k\times r:\frac{1}{2}\times 5k\times r\\ =& 3:4:5\end{array}$

Hence, the answer is $3:4:5$

Example 3: In a triangle, $\mathrm{ABC}\frac{4b^2{c}^2-(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8b^2{c}^2}$ is equal to.
Solution

$\begin{array}{rl}& \frac{4b^2{c}^2-(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8b^2{c}^2}\\ & =\frac{1}{2}-\frac{(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8b^2{c}^2}\\ & =\frac{1}{2}-\frac{2s\times 2\times (s-a)\times 2\times (s-b)\times 2\times (s-c)}{8b^2{c}^2}\\ & =\frac{1}{2}-\frac{2s\times (s-a)\times (s-b)\times (s-c)}{b^2{c}^2}\\ & =\frac{1}{2}-\frac{2{\mathrm{\Delta }}^2}{b^2{c}^2}\\ & =\frac{1}{2}-\frac{2{(\frac{1}{2}bc\sin A)}^2}{b^2{c}^2}\\ & =\frac{1}{2}{\cos }^{2}A\end{array}$

Hence, the answer is $\frac{1}{2}{\cos }^{2}A$

Example 4: If the sides of a triangle are the roots of the equation $x^3-4x^2+5x-2=0$, then the area of this triangle.
Solution

$\begin{array}{rl}& x^3-4x^2+5x-2=0\\ & (x-2)(x^2-2x+1)=0\\ & (x-2)(x-1{)}^2=0\\ & a=2,b=1,c=1\end{array}$

As $b+c=a$, it is not a triangle and the vertices are lying on a line
So, area $=0$
Hence, the answer is 0

Example 5: If in a $\mathrm{△}ABC$, the altitudes from the vertices $A,B,C$ on opposite sides are in H .P, then $\sin A,\sin B,\sin C$ are in:

Solution: Let the altitudes be $AD,BE$, and $CF$.
Now, the Area of the triangle $=\frac{1}{2}($ Base $)($ Height $)$
So $\frac{1}{2}(AB)(CF)=\frac{1}{2}(BC)(AD)=\frac{1}{2}(AC)(BE)=k($ say $)$
$AD=$ $ha$ altitude from $a$
then $\frac{1}{2}aha=\frac{1}{2}bhb=\frac{1}{2}chc$
Thus $a=\frac{k}{ha},b=\frac{k}{hb},c=\frac{k}{hc}$

when k= is some content --------(1)

Now $ha,hb,hc$ in HP

$\Rightarrow \frac{2}{hb}=\frac{1}{ha}+\frac{1}{hc}----(2)$

(1) and (2) we get

$\begin{array}{rl}& 2b=a+c,\text{ here }\\ & =A\cdot P\end{array}$

Hence, the answer is $\sin A,\sin B,\sin C$ are in the AP