Trigonometric functions describe the relationship between angles and sides of a triangle and help in solving problems involving heights and distances. They form an important part of mathematics and are widely used in physics, engineering, and other real-life applications.
Trigonometric Functions
Have you ever wondered how engineers measure the heights of buildings, how astronomers calculate distances of stars, or how angles and distances are connected in real life? All these calculations are made possible using trigonometric functions, which play a key role in mathematics and science. Starting from Trigonometric Functions in Class 10 and till Class 12, these functions describe the relationship between angles and sides of a triangle. In Class 12, trigonometric functions are studied in greater depth, including their domains and ranges, graphs, formulas, derivatives, integrals, and inverse trigonometric functions. For example, using sine and cosine functions, we can find the height of a tower or the distance of an object without measuring it directly.
This Story also Contains
- Trigonometric Functions in Mathematics
- Domain and Range of Trigonometric Functions
- Graph of Trigonometric Functions
- Trigonometric Functions Identities
- Inverse Trigonometric Functions
- Differentiation of Trigonometric Functions
- Integration of Trigonometric Functions
- Solved Previous Year Questions on Trigonometric Functions
- List of Topics related to Trigonometric Functions according to NCERT/JEE Mains
- Trigonometric Functions in Different Exams
- NCERT Resources for Trigonometric Functions
- Important Books for Trigonometric Functions
- NCERT Subject-Wise Resources
- Practice Questions based on Trigonometric Functions
- Conclusion
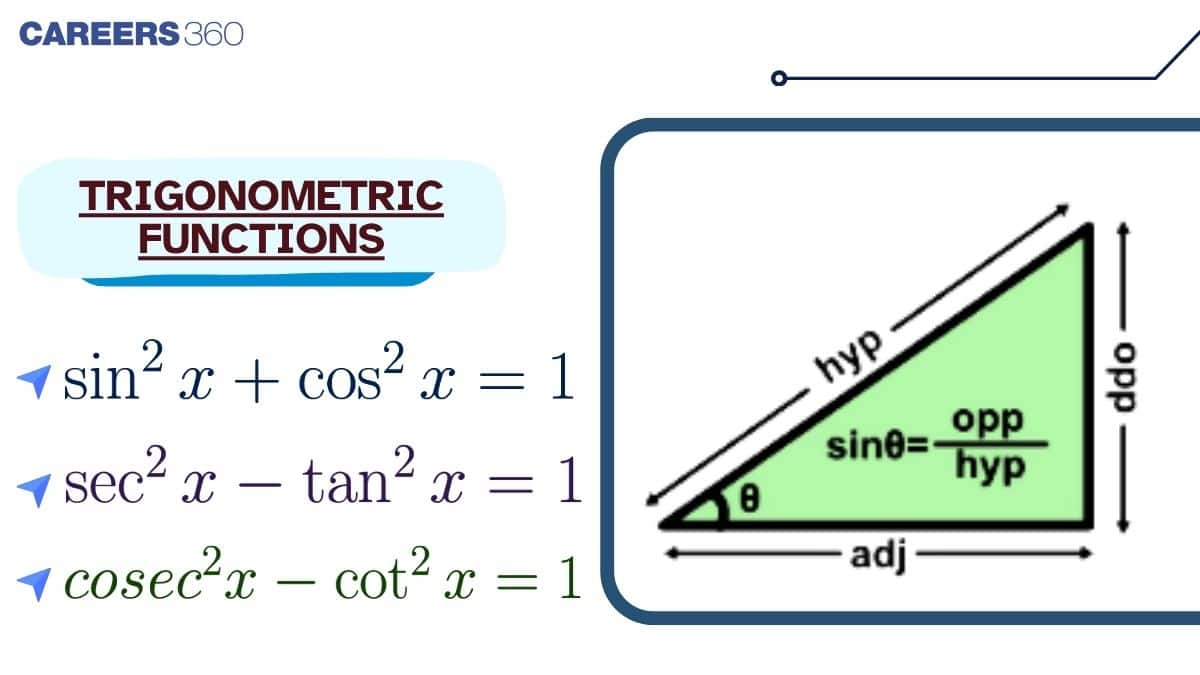
Trigonometric functions also have many real-life applications. They are used in physics to study waves and motion, in engineering for designing structures, and in navigation and astronomy to accurately calculate angles and distances. In this article, you will find clear explanations of trigonometric function formulas, values of trigonometric functions, derivatives and differentiation of inverse trigonometric functions, along with ready-to-use trigonometric tables. These simplified explanations are designed to strengthen your concepts and help you solve exam-oriented problems with confidence.
Trigonometric Functions in Mathematics
Origin of Trigonometry
Trigonometry, in its simplest form, is the study of triangles with angles and lengths on their sides. When we break down the word trigonometry, we find that 'Tri' is a Greek word that means three, 'Gon' means length, and 'metry' means trigonometric formulas measurement.'
What are Trigonometric Functions?
In trigonometry, there are six basic trigonometric functions. These functions are trigonometric ratios that are based on ratios of sides in a right triangle: the hypotenuse (the longest side), the base (the side adjacent to a chosen angle), and the perpendicular (the side opposite the chosen angle). These functions are sine, cosine, tangent, secant, cosecant, and cotangent. They help us find different values in triangles by comparing these side lengths.

Trigonometric Functions Formulas
The trigonometric functions formulas are:
1. Sine ($\sin$)- $\sin$ is defined as a ratio of the side opposite to that angle (perpendicular) and hypotenuse.
$\sin t=\frac{\text { opposite }}{\text { hypotenuse }}$
2. Cosine ($\cos$) - $\cos$ is defined as the ratio of the side adjacent to that angle (base) and the hypotenuse.
$\cos t=\frac{\text { adjacent }}{\text { hypotenuse }}$
3. Tangent ($\tan$) - $\tan$ is defined as the ratio of the side opposite to that angle (perpendicular) and the side adjacent to that angle (base).
$\tan t=\frac{\text { opposite }}{\text { adjacent }}$
4. cotangent ($\cot$) - $\cot$ is defined as the ratio of the side adjacent to that angle (base) and the side opposite to that angle (perpendicular). It is the reciprocal of tan.
$\cot t=\frac{\text { adjacent }}{\text { opposite }}$
5. secant ($\sec$) - $\sec$ is defined as the ratio of the hypotenuse and the side adjacent to that angle (base). It is the reciprocal of cos.
$\sec t=\frac{\text {hypotenuse }}{\text { adjacent }}$
6. Cosecant ($\operatorname{cosec}$) - $\operatorname{cosec}$ is defined as the ratio of the hypotenuse and the side opposite to that angle (perpendicular). It is the reciprocal of the sin.
$\operatorname{cosec} t=\frac{\text { hypotenuse }}{\text { opposite }}$
Values of Trigonometric Functions
In the trigonometric functions table, we use the values of trigonometric ratios for standard angles $0°, 30°, 45°, 60°,$ and $90°$. It is easy to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles.
Below are the trigonometric ratios of some special angles $0°, 30°, 45°, 60°,$ and $90°$.

Domain and Range of Trigonometric Functions
Understanding the domain and range of trigonometric functions is essential for solving problems in mathematics, physics, and engineering. The domain of a function is the set of all input values (usually $x$) for which the function is defined, while the range is the set of all possible output values (usually $y$).
Domain and Range of Basic Trigonometric Functions
| Function | Domain | Range | Remarks / Special Cases |
|---|---|---|---|
| $\sin x$ | $(-\infty, \infty)$ | $[-1, 1]$ | Defined for all real numbers |
| $\cos x$ | $(-\infty, \infty)$ | $[-1, 1]$ | Defined for all real numbers |
| $\tan x$ | $x \neq \frac{\pi}{2} + n\pi, n \in \mathbb{Z}$ | $(-\infty, \infty)$ | Undefined where $\cos x = 0$ |
| $\cot x$ | $x \neq n\pi, n \in \mathbb{Z}$ | $(-\infty, \infty)$ | Undefined where $\sin x = 0$ |
| $\sec x$ | $x \neq \frac{\pi}{2} + n\pi, n \in \mathbb{Z}$ | $(-\infty, -1] \cup [1, \infty)$ | Reciprocal of $\cos x$ |
| $\operatorname{cosec} x$ | $x \neq n\pi, n \in \mathbb{Z}$ | $(-\infty, -1] \cup [1, \infty)$ | Reciprocal of $\sin x$ |
Special Cases and Restrictions:
-
Functions like $\tan x$ and $\sec x$ are undefined wherever $\cos x = 0$.
-
Functions like $\cot x$ and $\operatorname{cosec} x$ are undefined wherever $\sin x = 0$.
-
The range of $\sin x$ and $\cos x$ is always between -1 and 1.
-
Knowing these domains and ranges is crucial before applying derivatives of trigonometric functions or solving equations involving trigonometric identities.
This knowledge also helps in plotting the graph of trigonometric functions and understanding their behaviour in different intervals.
Graph of Trigonometric Functions
The graphs of trigonometric functions are:
Sine ($\sin$)
$y = f(x) = \sin x$

Domain is $R$
Range is $[-1,1]$
We observe that $\sin x$ completes one full cycle of its possible values (from $-1$ to $1$ )
in the interval of length $2 \pi$.
So, the period of $\sin x$ is $2 \pi$.
The graph drawn in the interval $[0,2 \pi]$ repeats to the right and the left.
$\operatorname{Sin} x$ passes the graph as $\sin x=0$
So, The root of $y=\sin x$ is $n \pi$ where
$
n=\ldots \ldots-3,-2,-1,0,1,2,3,4 \ldots \ldots
$
Min value of $\sin x=-1$ at $=3 \pi / 2$
The max value of $\sin x=1$ at $\pi / 2$
Amplitude $=1$
$
\sin (-x)=-\sin x
$
So, $\sin \mathrm{x}$ is an odd function.
Cosine ($\cos$)
$y = f(x) = \cos x$

$
\sin (x+90)=\cos x
$
So, the $\cos x$ graph is drawn by shifting the $\sin \mathrm{x}$ graph by $90$ degrees.
Domain is $R$
Range is $[-1,1] \cos x=\pi / 2$. So, The root of $y=\cos x$ is $n(\pi / 2)$ where
$
n=\ldots \ldots-3,-2,-1,1,2,3,4 \ldots \ldots
$
Min value of $\cos x=-1$ at $2 \pi$
The max value of $\cos x=1$ at $0$ and $4 \pi$
Amplitude $=1$
Line of Symmetry $=\mathrm{Y}$ - axis
$
\cos (-x)=\cos x
$
So, $\cos x$ is an even function
Tangent ($\tan$)
$y=f(x) = \tan x$

Domain is $\mathbb{R}-\left\{\frac{(2 \mathrm{n}+1) \pi}{2}, \mathrm{n} \in \mathbb{I}\right\}$
Range is $R$
We observe that $\tan x$ increase in each of the intervals $\ldots$ $(-3 \pi / 2,-\pi / 2),(-\pi / 2, \pi / 2),(\pi / 2,3 \pi / 2) \ldots \ldots$.
The graph goes from negative to positive infinity. Period $=180$ degree $=\pi$. The root of the function $y=\tan x$ is $n \pi$ where $\mathrm{n}=\ldots \ldots-3,-2,-1,1,2,3 \ldots \ldots$
The amplitude is undefined as the graph tends to infinity.
Line of symmetry $=$ origin
$
\tan (-x)=-\tan x
$
So, the tangent function is odd.
Cosecant($\operatorname{cosec}$)
$ y= f(x) = \operatorname{cosec} x$

Domain is $\mathrm{R}-\{\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}$ (Integers) $\}$
Range is $R-(-1,1)$
As the curve repeats after an interval of $2 \pi$, the period of the cosecant function is $2 \pi$.
The amplitude of the graph of a cosecant function is undefined, as the curve does not have a maximum or a minimum value and tends to infinity.
Line of symmetry = origin
Vertical asymptotes are $x=n \pi$
$
\operatorname{cosec}(-x)=-\operatorname{cosec} x
$
So, $\operatorname{cosec} x$ is an odd function.
Secant ($\sec$)
$y=f(x)= \sec x$

Domain is $\mathbb{R}-\left\{\frac{(2 \mathrm{n}+1) \pi}{2}, \mathbf{n} \in \mathbb{I}\right\}$
The range is $R-(-1,1)$
The amplitude of the graph of a secant function is undefined, as the curve does not have a maximum or a minimum value and tends to infinity. As the curve repeats after an interval of $2 \pi$, the period of the function is $2 \pi$.
Line of Symmetry $=\mathrm{Y}$-axis
Vertical asymptotes $=\mathrm{x}=(2 \mathrm{n}+1) \pi / 2$
$\operatorname{Sec}(-x)=\sec x$
So, it is an even function
Cotangent ($\cot$)
$y=f(x)= \cot x$

Domain is $\mathrm{R}-\{\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}$ (Integers) $\}$
Range is $R$
The graph goes from negative to positive infinity.nWe observe that $\cot x$ decreases in each of the intervals $\ldots(-2 \pi /,-\pi),(-\pi, 0),(0, \pi) \quad$
The root of the equation $y=\cot x$ is $n \pi / 2$ where $n=\quad-3,-2,-1,1,2,3 . \quad$
The amplitude is undefined as the graph tends to infinity.
As the curve repeats after an interval of $\pi$, the period of the cotangent function is $\pi$. Line of symmetry $=$ origin
Vertical asymptotes are $x=n \pi$.
$\cot (-x)=-\cot x$
So it is an odd function.
Trigonometric Functions Identities
In trigonometry, identities help solve a variety of problems efficiently. These formulas are essential for tackling complex questions and provide fundamental resources for quick solutions. Below are the main trigonometric identities:
1. Pythagorean Identities
Trigonometric identities based on Pythagoras’ theorem:
$ \sin^2 t + \cos^2 t = 1 $
$ 1 + \tan^2 t = \sec^2 t $
$ 1 + \cot^2 t = \operatorname{cosec}^2 t $
$ \tan t = \frac{\sin t}{\cos t}, \quad \cot t = \frac{\cos t}{\sin t} $
2. Reciprocal Identities
$ \operatorname{cosec} t = \frac{1}{\sin t} $
$ \sec t = \frac{1}{\cos t} $
$ \cot t = \frac{1}{\tan t} $
3. Addition of Angles Identities
For two angles $A$ and $B$:
$ \sin(A+B) = \sin A \cos B + \cos A \sin B $
$ \cos(A+B) = \cos A \cos B - \sin A \sin B $
$ \tan(A+B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} $
4. Difference of Angles Identities
$ \sin(A-B) = \sin A \cos B - \cos A \sin B $
$ \cos(A-B) = \cos A \cos B + \sin A \sin B $
$ \tan(A-B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} $
5. Double Angle Identities
$ \sin 2A = 2 \sin A \cos A $
$ \cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A - 1 = 1 - 2 \sin^2 A $
$ \tan 2A = \frac{2 \tan A}{1 - \tan^2 A} $
6. Identities of Allied Angles
$ \sin(90-\theta) = \cos \theta, \quad \cos(90-\theta) = \sin \theta $
$ \tan(90-\theta) = \cot \theta, \quad \cot(90-\theta) = \tan \theta $
$ \sec(90-\theta) = \operatorname{cosec} \theta, \quad \operatorname{cosec}(90-\theta) = \sec \theta $
$ \sin(90+\theta) = \cos \theta, \quad \cos(90+\theta) = -\sin \theta $
$ \tan(90+\theta) = -\cot \theta, \quad \cot(90+\theta) = -\tan \theta $
$ \sec(90+\theta) = -\operatorname{cosec} \theta, \quad \operatorname{cosec}(90+\theta) = \sec \theta $
7. Triple Angle Identities
$ \sin 3A = 3 \sin A - 4 \sin^3 A $
$ \cos 3A = 4 \cos^3 A - 3 \cos A $
$ \tan 3A = \frac{3 \tan A - \tan^3 A}{1 - 3 \tan^2 A} $
$ \cot 3A = \frac{\cot^3 A - 3 \cot A}{3 \cot^2 A - 1} $
8. Supplementary Angle Identities
$ \sin(180-\theta) = \sin \theta, \quad \cos(180-\theta) = -\cos \theta $
$ \tan(180-\theta) = -\tan \theta, \quad \cot(180-\theta) = -\cot \theta $
$ \sec(180-\theta) = -\sec \theta, \quad \operatorname{cosec}(180-\theta) = \operatorname{cosec} \theta $
9. Sum-Product Identities
$ \sin C + \sin D = 2 \sin \frac{C+D}{2} \cos \frac{C-D}{2} $
$ \sin C - \sin D = 2 \cos \frac{C+D}{2} \sin \frac{C-D}{2} $
$ \cos C + \cos D = 2 \cos \frac{C+D}{2} \cos \frac{C-D}{2} $
$ \cos C - \cos D = -2 \sin \frac{C+D}{2} \sin \frac{C-D}{2} $
10. Identities of Opposite Angles
$ \sin(-A) = -\sin A, \quad \cos(-A) = \cos A $
$ \tan(-A) = -\tan A, \quad \cot(-A) = -\cot A $
$ \sec(-A) = \sec A, \quad \operatorname{cosec}(-A) = -\operatorname{cosec} A $
Inverse Trigonometric Functions
Inverse trigonometric functions “undo” the action of the original trigonometric functions. In other words, the domain of the inverse function is the range of the original function, and the range of the inverse function is the domain of the original function.
For example, if $f(x) = \sin x$, then its inverse is written as $f^{-1}(x) = \sin^{-1} x$. Note that $\sin^{-1} x$ is not the same as $\frac{1}{\sin x}$.
Examples of Inverse Trigonometric Functions
$ \sin(\frac {\pi}6) = \frac 12 \implies \frac {\pi}6 = \sin^{-1}(\frac 12) $
$ \cos(\pi) = -1 \implies \pi = \cos^{-1}(-1) $
$ \tan(\frac {\pi}4) = 1 \implies \frac {\pi}4 = \tan^{-1}(1) $
Domain and Range of Inverse Trigonometric Functions
| Function | Domain | Range |
|---|---|---|
| $y = \sin^{-1} x$ | $[-1, 1]$ | $[-\frac{\pi}2, \frac{\pi}2]$ |
| $y = \cos^{-1} x$ | $[-1, 1]$ | $[0, \pi]$ |
| $y = \tan^{-1} x$ | $\mathbb{R}$ | $(-\frac{\pi}2, \frac{\pi}2)$ |
| $y = \cot^{-1} x$ | $\mathbb{R}$ | $(0, \pi)$ |
| $y = \sec^{-1} x$ | $(-\infty, -1] \cup [1, \infty)$ | $[0, \pi] - {\frac{\pi}2}$ |
| $y = \operatorname{cosec}^{-1} x$ | $(-\infty, -1] \cup [1, \infty)$ | $[-\frac{\pi}2, \frac{\pi}2] - {0}$ |
Differentiation of Trigonometric Functions
The derivative of a trigonometric function gives the slope of the tangent to its curve. These formulas are essential for finding tangents, normals, or solving calculus problems.
$ \frac{d}{dx}(\sin x) = \cos x $
$ \frac{d}{dx}(\cos x) = -\sin x $
$ \frac{d}{dx}(\tan x) = \sec^2 x $
$ \frac{d}{dx}(\cot x) = -\operatorname{cosec}^2 x $
$ \frac{d}{dx}(\sec x) = \sec x \tan x $
$ \frac{d}{dx}(\operatorname{cosec} x) = -\operatorname{cosec} x \cot x $
Integration of Trigonometric Functions
Integration is used to calculate areas under curves of trigonometric functions or areas of irregular plane surfaces.
$ \int \sin x , dx = -\cos x + C $
$ \int \cos x , dx = \sin x + C $
$ \int \tan x , dx = \log |\sec x| + C $
$ \int \cot x , dx = \log |\sin x| + C $
$ \int \sec^2 x , dx = \tan x + C $
$ \int \operatorname{cosec}^2 x , dx = -\cot x + C $
$ \int \sec x \tan x , dx = \sec x + C $
$ \int \operatorname{cosec} x \cot x , dx = -\operatorname{cosec} x + C $
$ \int \sec x , dx = \log |\sec x + \tan x| + C $
$ \int \operatorname{cosec} x , dx = \log |\operatorname{cosec} x - \cot x| + C $
Solved Previous Year Questions on Trigonometric Functions
Solution: Given: $4 \sec A + 5 = 0$
$\Rightarrow \sec A = -\dfrac{5}{4}$
Since $ABCD$ is a convex quadrilateral, angle $A$ lies between $\dfrac{\pi}{2}$ and $\pi$ (i.e., second quadrant), where:
$\cos A < 0$
$\sin A > 0$
$\tan A < 0$
Now, $\sec A = \dfrac{1}{\cos A} = -\dfrac{5}{4}$
$\Rightarrow \cos A = -\dfrac{4}{5}$
Using identity: $\sin^2 A + \cos^2 A = 1$
$\Rightarrow \sin^2 A = 1 - \left(-\dfrac{4}{5}\right)^2 = 1 - \dfrac{16}{25} = \dfrac{9}{25}$
$\Rightarrow \sin A = \dfrac{3}{5}$ (positive in second quadrant)
Now, $\tan A = \dfrac{\sin A}{\cos A} = \dfrac{\dfrac{3}{5}}{-\dfrac{4}{5}} = -\dfrac{3}{4}$
$cosec A = \dfrac{1}{\sin A} = \dfrac{5}{3}$
Now, let the quadratic equation with roots $\tan A$ and $cosec A$ be:
$(x - \tan A)(x - cosec A) = 0$
Substitute values: $\left(x + \dfrac{3}{4}\right)\left(x - \dfrac{5}{3}\right) = 0$
Multiply: $x^2 - \dfrac{5}{3}x + \dfrac{3}{4}x - \dfrac{15}{12} = 0$
Combine terms: $x^2 - \left(\dfrac{5}{3} - \dfrac{3}{4}\right)x - \dfrac{15}{12} = 0$
$\Rightarrow x^2 - \dfrac{11}{12}x - \dfrac{15}{12} = 0$
Multiply throughout by 12 to remove denominators:
$12x^2 - 11x - 15 = 0$
Example 2: What is the range of $f(x)=\sin|3x^3| \ \ x\epsilon R$?
Solution: Graph of sine function
y = f(x) = sin(x)
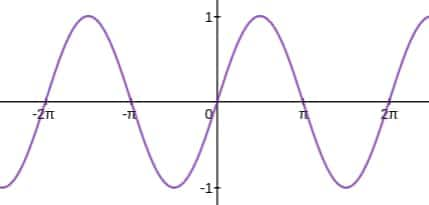
Now,
$f(x)=\sin \left|3 x^3\right|, \quad x \in R$
$\text { assume }\left|3 x^3\right|=t, \quad t \geq 0$
Now, from graph if $t \geq 0$, then $y=\sin (t)$ takes all values in $[-1,1]$ So, range is $[-1,1]$.
Example 3: The number of solutions of $\sin 3x = \cos 2x$, in the interval $\left(\frac{\pi}{2}, \pi\right)$ is: [JEE MAINS 2018]
Solution: We are given the equation: $\sin 3x = \cos 2x$
Using the identity: $\cos \theta = \sin\left(\frac{\pi}{2} - \theta\right)$
We rewrite the equation as: $\sin 3x = \sin\left(\frac{\pi}{2} - 2x\right)$
Now using the identity: If $\sin A = \sin B$, then
$A = B + 2n\pi$ or $A = \pi - B + 2n\pi$
Case 1: $3x = \frac{\pi}{2} - 2x + 2n\pi$
$\Rightarrow 5x = \frac{\pi}{2} + 2n\pi$
$\Rightarrow x = \frac{\pi + 4n\pi}{10}$
Case 2: $3x = \pi - \left(\frac{\pi}{2} - 2x\right) + 2n\pi$
$\Rightarrow 3x = \frac{\pi}{2} + 2x + 2n\pi$
$\Rightarrow x = \frac{\pi}{2} + 2n\pi$
Now find values of $x$ in the interval $\left(\frac{\pi}{2}, \pi\right)$
From Case 1: $x = \frac{(1 + 4n)\pi}{10}$
Try $n = 1$: $x = \frac{5\pi}{10} = \frac{\pi}{2}$ excluded
Try $n = 2$: $x = \frac{9\pi}{10} \in \left(\frac{\pi}{2}, \pi\right)$
Try $n = 3$: $x = \frac{13\pi}{10} > \pi$ not allowed
From Case 2: $x = \frac{\pi}{2} + 2n\pi$ all values exceed $\pi$ in the interval
So, only one solution exists.
Hence, the number of solutions is $1$.
Example 4: The value of $\cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots . .+\cos \frac{17 \pi}{19}$ is equal to (up to one decimal point):
1) $0.5$
2) $0$
3) $1$
4) $0.7$
Solution:
The trigonometric ratios for angles in all four quadrants.
$
\begin{aligned}
& \cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots .+\cos \frac{17 \pi}{19} \\
& \text { Here, } A=\frac{\pi}{19}, D=\frac{2 \pi}{19}, n=9 \\
& \because \cos A+\cos (A+D)+\cos (A+2 D)+\ldots \ldots . .+\cos (A+(n-1) D) \\
& =\frac{\sin \left(\frac{n D}{2}\right)}{\sin \frac{D}{2}} \cdot \cos \left(\frac{2 A+(n-1) D}{2}\right)=\frac{\sin 9 \times \frac{\pi}{19}}{\sin \frac{\pi}{19}} \times \cos \left(\frac{\frac{\pi}{19}+\frac{17 \pi}{19}}{2}\right) \\
& =\frac{\sin \frac{9 \pi}{19}}{\sin \frac{\pi}{19}} \times \cos \frac{9 \pi}{19} \\
& =\frac{1}{2} \cdot \frac{\sin \left(\frac{18 \pi}{19}\right)}{\sin \frac{\pi}{19}}=\frac{1}{2} \cdot \frac{\sin \frac{\pi}{19}}{\sin \frac{\pi}{19}}=\frac{1}{2}
\end{aligned}
$
Example 5: The value of the sum $\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)$ is
1) $\tan 2^n$
2) $\tan 2^n-1$
3) $\tan 2^n-\tan 1$
4) $\cos 2^n-\cos 2$
Solution:
$
\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)
$
$
\begin{aligned}
& \text { As } \sec \left(2.2^{k-1}\right)=\frac{1}{\cos \left(2.2^{k-1}\right)} \\
& =\sum_{k=1}^n \tan 2^{k-1} \times \frac{1+\tan ^2 2^{k-1}}{1-\tan ^2 2^{k-1}} \\
& =\sum_{k=1}^n\left(\frac{\tan (2)^{k-1}\left[2-1+\tan ^2 2^{k-1}\right]}{1-\tan ^2 2^{k-1}}\right) \\
& =\sum_{k=1}^n\left(\frac{2 \tan 2^{k-1}}{1-\tan ^2 2^{k-1}}-\tan (2)^{k-1}\right) \\
& =\sum_{k=1}^n\left(\tan 2^k-\tan 2^{k-1}\right) \\
& =\tan 2-\tan (1)+\tan 2^2-\tan 2+\ldots \tan 2^n-\tan 2^{n-1} \\
& =\tan 2^n-1
\end{aligned}
$
Hence, the answer is option 3.
List of Topics related to Trigonometric Functions according to NCERT/JEE Mains
This section provides a complete list of important trigonometric functions topics as per the NCERT and JEE Main syllabus. It helps you focus on the right areas for formulas, graphs, derivatives, and integration. Following this list ensures that you don’t miss any key concepts while preparing for exams.
Trigonometric Functions in Different Exams
Trigonometric Functions is a core chapter in mathematics and plays an important role in both school-level and competitive examinations. The table below highlights the exam-wise focus areas, frequently asked topics, and preparation strategies to help students prepare effectively and score well.
| Exam Name | Focus Area | Common Topics Asked | Preparation Tips |
|---|---|---|---|
| CBSE Board | Conceptual clarity & application | Trigonometric identities, domain and range, graphs, inverse trigonometric functions | Learn formulas thoroughly and practise NCERT examples |
| JEE Main | Problem-solving & accuracy | Trigonometric equations, identities, domain–range, inverse trigonometric functions | Practise MCQs and numerical problems regularly |
| JEE Advanced | Analytical thinking | Complex identities, trigonometric inequalities, inverse trigonometric proofs | Solve previous years’ advanced-level questions |
| NEET | Basics & speed | Trigonometric formulas, standard values, simple identities | Focus on quick formula application and revision |
| State Board Exams | Theory-oriented | Definitions, formulas, standard values, graphs | Revise textbook theory and solve in-text questions |
| Mathematics Olympiads | Concept application | Advanced identities, functional properties, trigonometric equations | Build strong fundamentals and practise challenging problems |
NCERT Resources for Trigonometric Functions
This section offers you the important NCERT resources for Class 11 Chapter 3 Trigonometric Functions. You'll get detailed notes, step-by-step NCERT solutions, and NCERT Exemplar problems, making it simple to master Trigonometric Ratios.
Important Books for Trigonometric Functions
This section lists the best books for studying trigonometric functions, covering formulas, graphs, etc. These books provide clear explanations and plenty of practice questions to strengthen your concepts and exam preparation.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Mathematics Textbook (Class 11) | NCERT | Official textbook; covers the fundamentals of trigonometric functions in a clear, accessible way. Essential for exams and foundational concepts. |
| Trigonometry | S. L. Loney | A classic reference with deep explanations and a wide range of problems, perfect for additional practice and conceptual clarity. |
| Cengage Maths (Trigonometry volume) | Cengage Learning | Illustrative text and rigorous problem sets focusing on competitive exam preparation (JEE Main/Advanced). |
| RD Sharma Mathematics (Class 11 & 12) | RD Sharma | Contains topic-wise solved examples and exercises for building and reinforcing concepts. |
NCERT Subject-Wise Resources
This section provides NCERT subject-wise resources for helping you study each topic for each subject clearly. It includes explanations, examples, and practice questions to build a strong foundation.
| Resource Type | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT Notes Class 11 Maths | NCERT Notes Class 11 Physics | NCERT Notes Class 11 Chemistry |
| NCERT Solutions | NCERT Solutions for Class 11 Mathematics | NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Practice Questions based on Trigonometric Functions
This section offers practice questions on trigonometric functions to help you apply formulas, derivatives, and graphs. Solving these problems will improve your understanding and prepare you for exams like JEE Main.
Conclusion
Trigonometric Functions form a vital part of mathematics and have wide applications in science, engineering, and everyday problem-solving. A clear understanding of formulas, identities, graphs, and inverse trigonometric functions helps students solve problems with confidence. Regular practice and proper revision are key to mastering this chapter. With strong basics, students can easily handle advanced topics and perform well in board and competitive exams.
Frequently Asked Questions (FAQs)
The six basic trigonometric functions are $\sin$, $\cos$, $\tan$, $\cot$, $\sec$, and $\csc$, which relate the sides of a right-angled triangle to its angles.
$\cos$ is positive in Quadrant I and Quadrant IV of the coordinate plane.
The value of $\sin 120° = \sin(180° - 60°) = \sin 60° = \sqrt{3}/2$.
Trigonometric functions class 11 covers the study of $\sin$, $\cos$, $\tan$, and other ratios, their properties, formulas, graphs, and applications in triangles.
Quadrant 4 is where x-values are positive and y-values are negative, so $\cos$ and $\sec$ are positive, while $\sin$, $\csc$, $\tan$, and $\cot$ are negative.
The 6 basic trigonometric functions are sine($\sin$), cosine($\cos$), tangent($\tan$), cosecant($\csc$), secant($\sec$) and cotangent($\cot$).
