Binomial Theorem for any Index

The binomial theorem for any index is an important concept in mathematics that allows to expand expression with real or complex exponent. It is difficult to solve the powers manually therefore this expression makes it simpler to solve. This theorem is widely used in real-life applications in mathematics including calculus etc.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Binomial Expression:
2. Binomial Theorem for any Index
3. Solved Examples Based on Binomial Theorem for any Index:

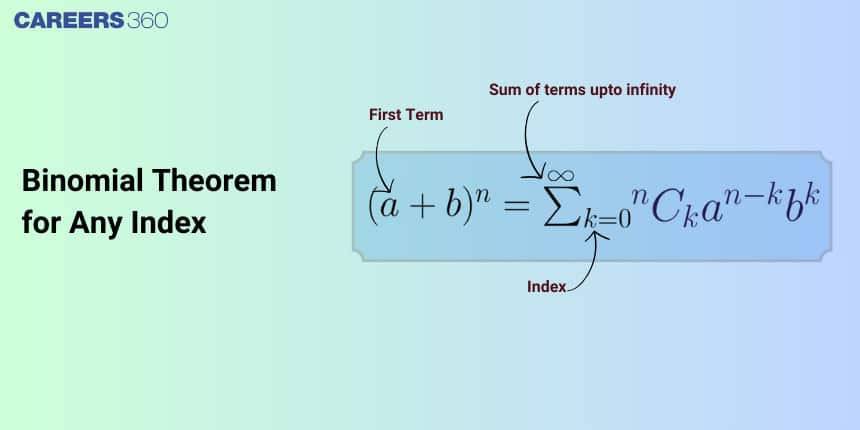
What is Binomial Expression:

$\begin{aligned}
&\text { An algebraic expression consisting of only two terms is called a Binomial Expression }\\
&e g \cdot(a+b)^2,\left(\sqrt{x}+\frac{k}{x^2}\right)^5,(x+9 y)^{-2 / 3}
\end{aligned}$

Binomial Theorem for any Index

Statement: If $n$ is a rational number and $x$ is a real number such that $|\mathrm{x}|<1$, then,

$ (1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\frac{n(n-1)(n-2) \ldots \ldots(n-r+1)}{r!} x^r \ldots $

Proof:

Let $f(x)=(1+{{x}})^{{n}}=a_0+a_1 x+a_2 x^2+\ldots+a_1 x^n+\ldots$

$ {{f}(0)}=(1+{{0}} {{{n}}}=1 $

Differentiating (1) w.r.t. $x$ on both sides, we get

$ =a_1+2 a_2 x+3 a_3 x^3+4 a_4 x^3+\ldots+r a_1 x^r-1+\ldots(2) $

Put $x=0$, we get $n=a_1$

Differentiating (2) w.r.t. $\times$ on both sides, we get

$ =2 a_2+6 a_3 x+12 a_4 x^2+\ldots+r(r-1) a_4 x^h-2+\ldots $

Put $x=0$, we get $a_2=[n(n-1)] / 2$ !

Differentiating (3), w.r.t. x on both sides, we get

Put $x=0$, we get $a_3=[n(n-1)(n-2)] / 3$ !

Similarly, we get $a_4=[n(n-1)(n-2)(n-3)] / r!$ and so on

$ \therefore a_n=[n(n-1)(n-2) \ldots(n-r+1)] / r! $

Putting the values of $a_0, a_1, a_2, a_3, \ldots, a_n$ obtained in (1), we get

$ \left(1+x n=1+n x+[\{n(n-1)\} / 2!] x^2+[\{n(n-1)(n-2)\} / 2!] x^3+\ldots+[\{n(n-1)(n-2) \ldots(n-r+\right. $

1) $\} / r!] x^{4}+\ldots$

Hence proved the Binomial theorem of any index.

Results on Binomial Theorem of any Index

$ (1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\frac{n(n-1)(n-2) \ldots \ldots(n-r+1)}{r!} x^r \ldots $

In the above expansion replace ' $n$ ' with ' $-n$ '

$ (1+\mathrm{x})^{-\mathrm{n}}=1+(-\mathrm{n}) \mathrm{x}+\frac{(-\mathrm{n})((-\mathrm{n})-1)}{2!} \mathrm{x}^2+\frac{(-\mathrm{n})((-\mathrm{n})-1)((-\mathrm{n})-2)}{3!} \mathrm{x}^3+\ldots \ldots $

$\ldots+\frac{(-n)((-n)-1)((-n)-2) \ldots((-n)-r+1)}{r!} x^r \ldots \ldots \infty $

$\Rightarrow(1+\mathrm{x})^{-\mathrm{n}}=1-\mathrm{nx}+\frac{\mathrm{n}(\mathrm{n}+1)}{2!} \mathrm{x}^2-\frac{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}{3!} \mathrm{x}^3+\ldots \ldots $

$\ldots+(-1)^r \frac{n(n+1)(n+2) \ldots .(n+r-1)}{r!} x^r \ldots \ldots . \infty $

If $-n$ is a negative integer (so that $n$ is a positive integer), then we can re-write this expression as

$ =1-{ }^n C_1 x+{ }^{n+1} C_2 x^2-{ }^{n+2} C_3 x^3+\cdots+{ }^{n+r-1} C_r(-x)^r+\cdots $

$ (1-x)^{-n}=1+n x+\frac{n(n+1)}{2!} x^2+\frac{n(n+1)(n+2)}{3!} x^3+\cdots +\frac{n(n+1)(n+2) \cdots(n+r-1)}{r!} x^r+\cdots $

If $-n$ is a negative integer (so that $n$ is a positive integer), then we can re-write this expression as

$ =1+{ }^n C_1 x+{ }^{n+1} C_2 x^2+{ }^{n+2} C_3 x^3+\cdots+{ }^{n+r-1} C_r(x)^r+\cdots $

Important Note:

The coefficient of $x^5$ in $(1-x)^{-n}$, (when $n$ is a natural number) is ${ }^{n+r-1} C_r$

Some Important Binomial Expansion
1. $(1+x)^{-1}=1-x+x^2-x^3+\cdots$
2. $(1-x)^{-1}=1+x+x^2+x^3+\cdots$
3. $(1+x)^{-2}=1-2 x+3 x^2-4 x^3+\cdots$
4. $(1-x)^{-2}=1+2 x+3 x^2+4 x^3+\cdots$

Summary:

Understanding the binomial theorem is essential as it helps to solve the complex equation with powers easily. Binomial coefficients of the term equidistant from the beginning and end are equal. Knowledge of this concept helps to solve and analyze real-life complex problems.

Recommended Video :

Solved Examples Based on Binomial Theorem for any Index:

Example 1: Which of the following Binomial theorem is not possible?
1) $(x+y)^{\frac{-3}{4}}$
2) $\sqrt{(x+y)}$
3) $\sqrt{(x-y)}$
4) $(x+y)^{\frac{7}{3}}$

Solution
As we learnt
Condition for Binomial Theorem for Rational Index:
Here n is a negative integer or a fraction where $-1<n<1$, otherwise expansion will not be possible. for rational powers, we need $-1<n<1$.

Hence, the answer is the option 4.

Example 2: Find the cube root of $318$

1) $6.71$

2) $6.79$

3) $6.83$

4) $6.88$

Solution

The given series is

$
(1+\mathrm{x})^{\mathrm{n}}={ }^{\mathrm{n}} \mathrm{C}_0+{ }^{\mathrm{n}} \mathrm{C}_1 \mathrm{x}+{ }^{\mathrm{n}} \mathrm{C}_2 \mathrm{x}^2+\ldots .+{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}}+\ldots .+{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}}
$

for negative or fractional Index

$
(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\frac{n(n-1)(n-2) \ldots . .(n-r+1)}{r!} x^r \ldots \infty
$

Note:
1. If n is negative or fractional index then this condition $|\mathrm{x}|<1$ is essential.
2. There is an infinite number of terms in the expansion of $(1+x)^n$, when $n$ is negative or fractional index.

If the first term is not unity and the index of the binomial is either a negative integer or a fraction, then we expand as follows:

$
\begin{aligned}
(x+a)^n & =\left\{a\left(1+\frac{x}{a}\right)\right\}^n+a^n\left(1+\frac{x}{a}\right)^n \\
& =a^n\left\{1+n \frac{x}{a}+\frac{n(n-1)}{2!}\left(\frac{x}{a}\right)^2+\cdots\right\} \\
& =a^n+n a^{n-1} x+\frac{n(n-1)}{2!} a^{n-2} x^2+\cdots
\end{aligned}
$

The above expansion is valid when $\left|\frac{x}{a}\right|<1$.

$
\begin{gathered}
(318)^{1 / 3}=\left(7^3-25\right)^{1 / 3}=7\left(1-\frac{25}{7^3}\right)^{1 / 3} \\
=7\left(1-\frac{25}{3 \times 343}+\frac{1 \times 2}{3 \times 3 \times 2!}\left(\frac{25}{343}\right)^2+\ldots\right)=7(1-0.0243)=6.83
\end{gathered}
$
Hence, the answer is the option 3.

Example 3: If $0<\mathrm{x}<1$, then the first negative term in the expansion of $(1+x)^{\frac{2 \pi}{5}}$ is
1) $8^{\text {th }}$ term
2) $7^{\text {th }}$ term
3) $6^{\text {th }}$ term
4) $9^{\text {th }}$ term

Solution

Binomial Theorem for any index

For negative or fractional Index and $|x|<1$,

$
(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\frac{n(n-1)(n-2) \ldots \ldots(n-r+1)}{r!} x^r \ldots \infty
$
Now,
The first term is $1$ , so positive
The second term is also positive as both $n$ and $x$ are positive
In any term, $\underline{x}^r$ is positive, and $r!$ is positive. So, the factor that will make a term negative is $(n-r+1)$
So, we need to find $r$ when $(n-r+1)$ will be negative for the first time ( $r$ is an integer), where $n=27 / 5$
Solving $27 / 5-r+1<0$, we get $r>6.4$
So, $r=7$ and this happens in the 8th term, so the 8th term is the answer.
Hence, the answer is the option 1.

Example 4: Find the value of $\sqrt{\frac{y}{x+y}} \cdot \sqrt{\frac{y}{y-x}}$, if x is very small as compared to y .
1) $1-\frac{1}{2} \cdot \frac{y^2}{x^2}$
2) $1+\frac{1}{2} \cdot \frac{y^2}{x^2}$
3) $1-\frac{1}{2} \cdot \frac{x^2}{y^2}$
4) $1+\frac{1}{2} \cdot \frac{x^2}{y^2}$

Solution

Binomial Theorem for any index

For negative or fractional Index and $|x|<1$,

$
(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\ldots \ldots+\frac{n(n-1)(n-2) \ldots . .(n-r+1)}{r!} x^r \ldots \infty$

Now,

$
\begin{aligned}
\sqrt{\frac{y}{x+y}} \sqrt{\frac{y}{y-x}} & =\left(\frac{1}{1+\frac{x}{y}}\right)^{1 / 2}\left(\frac{1}{1-\frac{x}{y}}\right)^{1 / 2} \\
& =\left(1-\frac{x^2}{y^2}\right)^{-1 / 2}=1+\frac{1}{2} \cdot \frac{x^2}{y^2}
\end{aligned}
$

(ignoring higher powers of $x / y$ as $x / y$ is small)
Hence, the answer is the option 4.

For negative or fractional Index and $|x|<1$,

$
(1+x)^n=1+n x+\frac{n(n-1)}{2!} x^2+\frac{n(n-1)(n-2)}{3!} x^3+\ldots \ldots+\frac{n(n-1)(n-2) \ldots . .(n-r+1)}{r!} x^r \ldots \infty
$

Now,

$
\begin{aligned}
\sqrt{\frac{y}{x+y}} \sqrt{\frac{y}{y-x}} & =\left(\frac{1}{1+\frac{x}{y}}\right)^{1 / 2}\left(\frac{1}{1-\frac{x}{y}}\right)^{1 / 2} \\
& =\left(1-\frac{x^2}{y^2}\right)^{-1 / 2}=1+\frac{1}{2} \cdot \frac{x^2}{y^2}
\end{aligned}
$

(ignoring higher powers of $x / y$ as $x / y$ is small)
Hence, the answer is the option 4.

Example 5: To expand $(1+2 x)^{-1 / 2}$ as an infinite series, the range of $x$ should be
1) $\left[-\frac{1}{2}, \frac{1}{2}\right]$
2) $\left(-\frac{1}{2}, \frac{1}{2}\right)$
3) $[-2,2]$
4) $(-2,2)$

Solution
$(1+2 x)^{-1 / 2}$ can be expanded if $|2 x|<1$ i.e., if $|x|<\frac{1}{2}$ i.e., if $\quad-\frac{1}{2}<x<\frac{1}{2}$ i.e., if

$
x \in\left(-\frac{1}{2}, \frac{1}{2}\right)
$
Hence, the answer is the option (2).