Cardinal Numbers - Meaning, Examples, Sets

Cardinal Number of Set

A set is a well-defined collection of distinct objects or elements. These objects can be anything—numbers, letters, people, or even other sets. In set theory, sets are denoted by capital letters such as $A, B, C, S, U, V$, etc., and are widely used in mathematics to represent groups of objects sharing common properties. Now, let's explore an important concept within set theory: the cardinal number of a set.

What is the Cardinal Number of a Set?

In mathematics, the cardinal number of a set refers to the total number of distinct elements in that set. It helps quantify the size or count of a set and is especially useful when working with finite sets.

For example, in a cricket team, there are 11 players. The number $11$ represents the cardinal number of the set of players in the team.

The cardinal number of a set $A$ is denoted by $n(A)$.

If $A = \{1, 3, 7, 11, 13\}$, then the number of elements in $A$ is:

$n(A)=5$

Formula for Cardinal Number of the Union of Two Sets

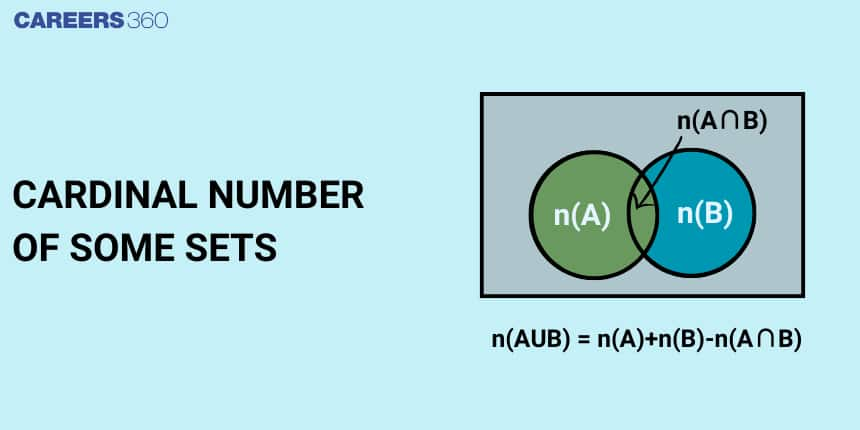
Given two finite sets $A$ and $B$, the number of elements in their union of sets is given by the formula:

n(A∪B)=n(A)+n(B)−n(A∩B)n(A \cup B) = n(A) + n(B) - n(A \cap B)n(A∪B)=n(A)+n(B)−n(A∩B)

If $A$ and $B$ are disjoint sets (i.e., $A \cap B = \varphi$), then:

$n(A \cup B) = n(A) + n(B)$

Formula for Cardinal Number of the Union of Three Sets

If $A$, $B$, and $C$ are any three finite sets, then the number of elements in their union is given by the inclusion-exclusion principle:

$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(A \cap C) + n(A \cap B \cap C)$

This formula helps avoid overcounting the elements that appear in more than one set.

Cardinal Number Notation and Terminology

• Symbol: $n(A)$ represents the cardinal number of set $A$.
• Finite set: A set with a countable number of elements.
• Infinite set: A set with elements that cannot be counted (like natural numbers).
• Empty set: The cardinal number of the empty set $\varphi$ is $0$, i.e., $n(\varphi) = 0$.

Now that you've understood what the cardinal number of a set is, let’s go through some examples of the cardinal number of sets to reinforce the concept and practice applying the formulas.

Cardinal Number of Some Sets Examples

Understanding the cardinal number becomes easier through simple examples. Here are a few sets with their corresponding cardinal numbers, calculated by counting the number of distinct elements in each set:

1. Let $A = \{1, 2, 6, 7, 4, 3, 5, 2, 8\}$
   Since each element is counted only once, even if repeated:
   $\Rightarrow n(A) = 8$
2. Let $B = \{a, d, c, t, r, v\}$
   All elements are unique:
   $\Rightarrow n(B) = 6$
3. Let $C = \{\}$ (an empty set)
   No elements in the set:

$\Rightarrow n(C) = 0$

4. Let $D = \{x, x, x, x\}$
   All elements are the same, so only one distinct element:
   $\Rightarrow n(D) = 1$
5. Let $E = \{apple, mango, banana, mango, orange\}$
   Remove duplicate "mango":
   $\Rightarrow n(E) = 4$

Cardinal Numbers of Sets Formula

To calculate the number of elements in sets, especially when they are disjoint or overlapping, we use specific cardinal number formulas. These formulas help in solving set problems efficiently in exams and real-life situations. Below are the standard formulas used for two or three sets:

For Two Sets:

• If sets are disjoint (no common elements):
  $n(A \cup B) = n(A) + n(B)$
• If sets are overlapping (some common elements):
  $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

For Three Sets:

• If sets are disjoint:
  $n(A \cup B \cup C) = n(A) + n(B) + n(C)$
• If sets are overlapping:
  $n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C)$

Important Notes on Cardinal Numbers:

• The collection of all ordinal numbers can be represented using cardinal numbers.
• Cardinal numbers can be expressed in words, such as one, two, three, etc.
• While cardinal numbers indicate "how many" elements are present in a set, ordinal numbers tell us the position or order (like first, second, third).

Difference between Cardinal and Ordinary Numbers

Cardinal numbers and ordinal numbers are both types of numbers used in mathematics and counting. Cardinal numbers represent the quantity or amount of objects or elements in a set, while ordinal numbers indicate the position or order of objects in a sequence. For example, the cardinal number "three" represents the quantity of three objects, while the ordinal number "third" indicates the position of an object in a sequence. While cardinal numbers are used for counting and measuring, ordinal numbers are used for ranking and ordering.

Cardinal Numbers of Empty, Singleton, and Universal Sets

In set theory and discrete mathematics, the cardinal number (cardinality) of a set tells us the number of elements present in that set. It is denoted by $|A|$ or $n(A)$.

Some special sets like the empty set, singleton set, and universal set have fixed or easily predictable cardinalities. These are very important in counting problems, probability, Venn diagrams, and basic set operations.

Here’s a clear comparison table for quick understanding.

Cardinality Table for Special Types of Sets

For Quick Understanding

• Empty set → nothing inside → cardinality is $0$

• Singleton set → one element → cardinality is $1$

• Universal set → everything → cardinality depends on total elements

Cardinality of Union and Intersection of Sets

In set theory and discrete mathematics, the cardinality of a set refers to the number of elements present in the set. It is denoted by $|A|$ or $n(A)$.

When we work with two or more sets, we often need to find the cardinality of their union or intersection. In simple words:

• Union → total distinct elements from all sets combined

• Intersection → common elements shared between sets

Understanding the cardinality of union and intersection of sets is extremely important for solving counting problems, probability questions, surveys, and Venn diagram-based questions.

Cardinality of Union of Two Sets

The union of two sets includes all elements from both sets without repetition.

If we simply add $|A| + |B|$, we might accidentally count common elements twice.
So we subtract the intersection once.

Formula

$|A \cup B| = |A| + |B| - |A \cap B|$

Why do we subtract?

Because:

• $|A|$ counts common elements once

• $|B|$ counts them again

• So they are counted twice

Subtracting $|A \cap B|$ removes the extra counting.

Cardinality of Intersection of Two Sets

The intersection of sets contains only the elements common to both sets.

Formula

$|A \cap B|$ simply equals the number of common elements between $A$ and $B$.

No special adjustment is needed.

Example for Better Understanding

Let $A = \{1,2,3,4\}$
$B = \{3,4,5,6\}$

Then: $|A| = 4$
$|B| = 4$
$A \cap B = {3,4}$ so $|A \cap B| = 2$

Now apply formula:

$|A \cup B| = 4 + 4 - 2 = 6$

So the union has 6 distinct elements.

Cardinality of Union of Three Sets (Inclusion–Exclusion Principle)

When dealing with three sets, we extend the formula.

Formula

$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|$

Solved Examples Based On the Cardinal Number of Sets

Example 1: If $U$ is the universal set, $n(A)=50, n(B)=60$, and $n(A \cap B)=30$. The total elements in the universal set is 200. Find $n\left(A^{\prime} \cap B^{\prime}\right)$
1) 80
2) 100
3) 120
4) 140

Solution:
$ \begin{aligned} & \mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})-\mathrm{n}(\mathrm{A} \cap \mathrm{B}) \\ & =50+60-30=80 \\ & n\left(A^{\prime} \cap B^{\prime}\right)=n(A \cup B)^{\prime}=200-80=120 \end{aligned} $
Hence, the answer is 120.

Example 2: Given $n(A)=50, n(B)=30$ and $n(A U B)=x$ such that $n(A \cap B)=$20. Find $x$:
1) 20
2) 40
3) 60
4) 80
Solution:
We know,
$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\ & x=50+30-20=60 \end{aligned} $
Hence, the answer is 60.

Example 3: The sum of integers from 1 to 100 that are divisible by 2 or 5 is
1) 3000
2) 3050
3) 3600
4) 3250

Solution:
Number of Elements in Union $A$ & $B$ -
$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B)\end{aligned} $
wherein
Given $A$ and $B$ are any finite sets. then the Number of Elements in union $A$ & $B$ is given by this formula.
$ \begin{aligned} & S=2+4+5+6 \\ & =(\text { sum of integers divisible by } 2)+(\text { sum of integers divisible by } 5)-(\text { sum of integers divisible by } 10(5 \times 2)) \\ & =(2+4+6+8 \ldots \ldots . .100)+(5+10+15 \ldots \ldots .100)-(10+20+\ldots \ldots \ldots+10) \\ & \text { sum of } n \text { term of an } A P \\ & =\frac{n}{2}(a+l) \\ & a=\text { first term } \\ & l=\text { last term } \\ & =\frac{50}{2}(2+100)+\frac{20}{2}(5+100)-\frac{10}{2}(10+100) \\ & =2550+1050-550=3050 \end{aligned} $
Hence, the answer is 3050.

Example 4: $ \text { If } A \cap B=\phi, n(A)=50, n(B)=70 \text {. Then evaluate } n(A \cup B) \text {. }$
1) 50
2) 70
3) 20
4) 120

Solution:
$\begin{equation} \begin{aligned} &\text { We know, }\\ &\begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\ & \text { Since } A \cap B=\phi, n(A \cap B)=0 \\ & n(A \cup B)=50+70-0=120 \end{aligned} \end{aligned} \end{equation}$
Hence, the answer is 120.

Example 5: In a class of 140 students numbered 1 to 140, all even-numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course, and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is :
1) 102
2) 42
3) 1
4) 38

Solution:
Number of Elements in Union $A, B$ & $C$ -
$ \begin{aligned} & n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \\ & \cap B \cap C) \\\end{aligned} $
wherein
Given $\mathrm{A}, \mathrm{B}$, and C are any finite sets. then the Number of Elements in union $A$ , $B$ & $C$ is given by this formula.
From the concept,
Let $n(M)=$ no. of students opted maths $=70$
$n(P)=$ student opted physics $=40$
$\mathrm{n}(\mathrm{C})=$ student opted chemistry $=28$
$n(M \cap P)=$ number of students opted for physics and maths $=23$
$n(M \cap C)=$ number of students opted for maths and chemistry = 14
$n(P \cap C)=$ number of students opted for physics and chemistry $=9$
$n(M \cap P \cap C)=$ number of students opted for all three students $=4$
So the total number of students who opted for at least one subject $=$
$n(M \cup P \cup C)=n(M)+n(P)+n(C)-n(M \cap P)-n(M \cap C)-n(P \cap C)+n(M \cap P \cap C)$
So putting the values, we have
$n(M \cup P \cup C)=70+46+28-23-14-9+4=102$
Hence total no. of students who have not adopted any course $=$ total number of students -total number of students who opted for at least one course $=140-$ $102=38$
Hence, the answer is 38.

List of Topics Related to Cardinal Numbers of Some Sets

Understanding the cardinal number of sets becomes easier when you explore its related foundational concepts. From the roster and set-builder forms to universal sets, subsets, De Morgan’s laws, and more, each topic builds the groundwork for mastering set theory. In this section, we’ve listed all the essential topics linked to the cardinal numbers of some sets to help you revise key ideas and strengthen your conceptual clarity.

NCERT Resources

Strengthen your understanding of Class 11 Sets with high-quality NCERT study materials, designed to align with board exam patterns and competitive exam needs. These NCERT resources include detailed solutions, quick revision notes, and well-curated exemplar problems to support concept clarity and practice. Access all the key materials for NCERT Chapter 1 Sets below.

NCERT Solutions for Class 11 Chapter 1 Sets

NCERT Notes for Class 11 Chapter 1 Sets

NCERT Exemplar for Class 11 Chapter 1 Sets

Practice Questions on Cardinal Number of a Set

Consistent practice is key to mastering the concept of the cardinal number of a set in mathematics. These carefully designed practice questions will help you revise important formulas, understand core properties, and apply them in different contexts. Whether you're preparing for board exams or competitive tests, solving a cardinal number of set MCQs will boost your accuracy and confidence. Attempt the questions below and explore more practice topics from the Sets chapter.

Practice Here: Cardinal Number Of Some Sets - Practice Question MCQ.

You can practice some important topics of Sets below: