Sets (Maths) - Definition, Types, Symbols & Examples
Have you ever noticed how we naturally group things in daily life, for example, arranging books on a shelf, separating fruits in the kitchen, or keeping coins of the same value together? Mathematics uses the same idea, and such well-defined collections are called Sets. A set is defined as a well-defined collection of objects, where each object is called an element of the set. “Well-defined” means there is no confusion about whether an object belongs to the set or not. For example, the collection of all even numbers less than 10 is a set because we can clearly decide which numbers belong to it. The primary objective of these Sets notes is to equip students with clear concepts and essential study material, enabling them to understand the topic thoroughly and solve exercises independently with confidence.
This Story also Contains
- Sets in Mathematics
- Important Formulae of Sets
- Properties of Sets
- List of related topics to Sets according to NCERT/JEE Main
- Sets in Mathematics: Solved Previous Year Questions
- How to Study Sets Effectively?
- Some Basic Concepts of Sets in Different Exams
- Recommended Books for Sets
- NCERT Resources for Sets
- NCERT Subject-Wise Resources
- Practice Questions on Sets
- Conclusion
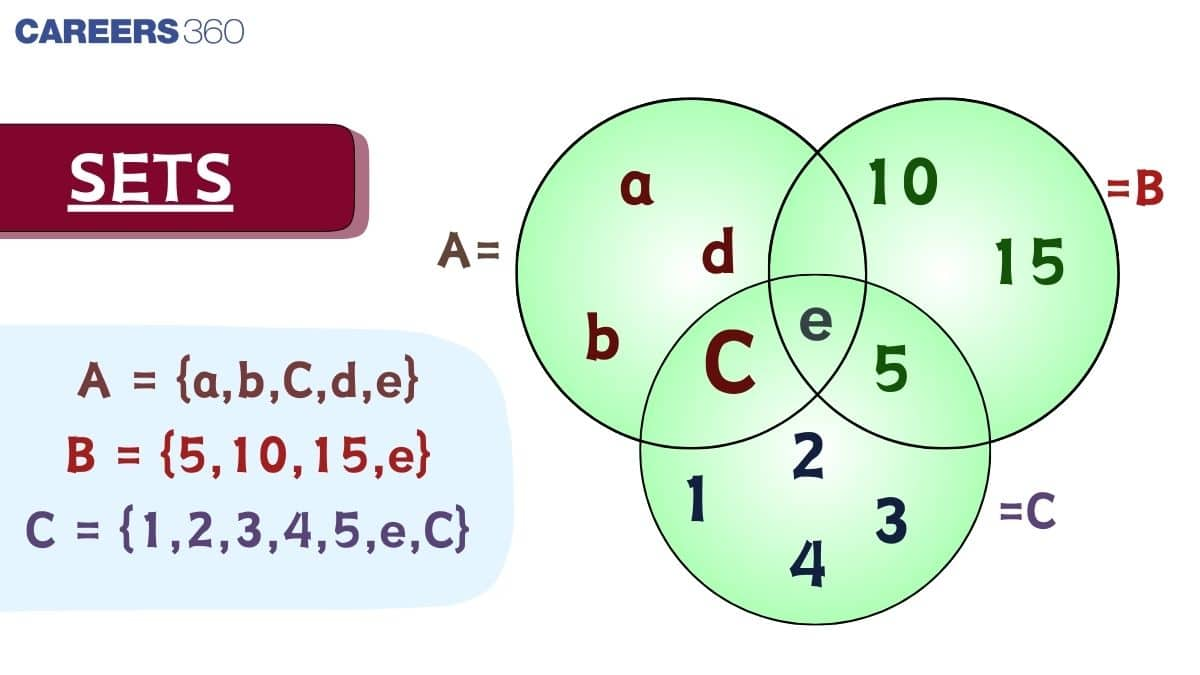
Sets are not limited to numbers alone. They appear frequently in real life. The collection of students in a classroom, the set of vowels in the English alphabet, or the set of all months in a year are common examples of Sets we use without realising it. The concept of Sets forms the foundation of higher mathematics. Topics such as relations, functions, probability, and statistics are all built using set theory. That is why understanding Sets properly in Class 11 is very important. In this article, you will learn what a set is, different ways to represent Sets, types of Sets, important set symbols, and simple examples that will help you understand the concept clearly and build a strong base for advanced chapters.
Sets in Mathematics
The concept of Sets is widely used in various branches of mathematics, such as algebra, probability, statistics, and calculus. A strong understanding of Sets in Class 11 makes it easier for students to grasp advanced topics like relations, functions, and probability in higher classes.
Importance of Sets
The concept of a set is one of the most basic yet important ideas in mathematics. Sets are used in defining relations, functions, geometry, sequences, probability, and more. This makes them a part of almost every branch of mathematics. The theory of Sets was introduced by Georg Cantor (1845–1918) while working on “trigonometric series problems.” In this chapter, you will learn Sets definition with examples, types of Sets in mathematics, representation of Sets, and Sets math examples with answers to build a strong foundation.
Although exams like JEE Main usually include only one question from Sets, understanding this topic is essential. It might seem simple, but when applied to functions, relations, and other areas, it becomes a crucial concept.
Definition of Sets
A set is a collection of well-defined objects. The objects which are in the set are called the elements of a set.
Example: Let us consider $A$ as the set of all natural numbers till $7$. So, set $A = \{1,2,3,4,5,6,7\}$.
Elements of Set
The objects which are in the set are called the elements of a set.
Example: Let us consider $A$ as the set of all natural numbers till $7$. So, set $A = \{1,2,3,4,5,6,7\}$.
Here $1,2,3,4,5,6,7$ are the elements of set $A$.
If $a$ is an element of set $A$, it can be said “$a$ belongs to $A$” and represented using $\in$ in place of ‘belongs to’. It can be represented as $a \in A$.
Order of Sets
Order of a set is also known as the cardinality of a set. The number of elements in a set is called its cardinal number or cardinality of a set. It is denoted by $n(A)$. If $\mathrm{A}=\{\mathrm{a}, \mathrm{s}, \mathrm{d}\}$, then $n(A)=3$
and if $B=\left\{x: x^2=1\right\}$, then $B=\{1,-1\}$, and hence $n(B)=2$
Set Symbols
Set symbols are special mathematical notations used to represent sets and describe relationships between their elements in a short and precise way.

Representation of Sets
Sets can be represented in two ways, namely Roster and Set Builder Form.
Roster Form(Tabular form)
A roster form is one of the ways to represent a set. In this form, the elements of the set are listed implicitly within curly brackets($\{\}$).
Example: ${a,e, i,o,u}$ is the set of all vowels in the English alphabet.
The elements in roster form can be in any order (they don't need to be in ascending/descending order). An element is not generally repeated in the roster form of a set, i.e., all the elements are taken as distinct. For example, the set of letters forming the word 'SCHOOL' is $\{S,C,H,O,L\}$ or $\{O,H,L,S,C\}$.
Set-Builder Form
In set builder form, the set is defined using the common property of the elements. For example, If $Z$ contains all values of $x$ for which the condition $q(x)$ is true, then we write
$Z=\{x: q(x)\} \text { or } Z=\{x \mid q(x)\}$
Where, ': ' or '|' is read as 'such that'.
Difference between Roster and Set-Builder Form
| Aspect | Roster Form | Set-Builder Form |
|---|---|---|
| Definition | Lists all elements of the set explicitly. | Describes elements of the set using a property or rule. |
| Notation | $A = \{1, 2, 3, 4, 5\}$ | $A = \{x : x \text{ is a natural number less than 6}\}$ |
| Elements | All elements are written out. | Elements are defined by a condition or property. |
| Use | Useful for small Sets where elements can be listed easily. | Useful for large or infinite Sets where listing all elements is impractical. |
| Example | $B = \{2, 4, 6, 8\}$ | $B = \{x : x \text{ is an even number less than 10}\}$ |
Types of Sets
The types of Sets in mathematics are as follows,
1. Empty Set: A set that does not contain any element is called an empty set, void set or null set.
Eg. The set of mangoes in the basket of guavas.
2. Singleton Set: A set having only one element is called a singleton set.
Eg, Set of all whole numbers which are not natural numbers, which is $A = \{0\}$
3. Finite Set: An empty set or a set consisting of a finite number of elements of a set is called a finite set.
Eg. Set of all natural numbers less than $7$ that is $A = \{1,2,3,4,5,6\}$
4. Infinite Set: A set consisting of an infinite number of elements of a set is called an infinite set.
Eg. Set of all whole numbers which is $A=\{1,2,3,4,5,6,7,....\}$
5. Equivalent Set: Two Sets having the same number of elements are called equivalent Sets. For Sets $A$ and $B$, it is represented as $n(A) = n(B)$.
Eg. Let $A$ be the set of all natural numbers less than $6$ and $B$ be the set of all whole numbers less than $5$.
$A=\{1,2,3,4,5\}$
$B=\{0,1,2,3,4\}$
Here, $n(A) = 5$ and $n(B) = 5$
Therefore, the Sets $A$ and $B$ are equivalent Sets.
6. Equal Set: Two Sets having the exact elements in both Sets are called equal Sets. For Sets $A$ and $B$, it is represented as $A$ = $B$.
Eg. Let $A$ be the set of all natural numbers less than $6$ and $B$ be the set of all whole numbers greater than $0$ and less than $6$.
$A=\{1,2,3,4,5\}$
$B=\{1,2,3,4,5\}$
Here, $A = B$
Therefore, the Sets $A$ and $B$ are equal Sets.
7. Disjoint set: Two Sets $A$ and $B$ are disjoint if they do not have any common element. That is, $A$ and $B$ are disjoint if $A \cap B=\emptyset$. (i.e) Two Sets are said to be disjoint if each set has distinct elements in it.
e.g. Let $A$ be the set of all natural numbers and $B$ be the set of all integers less than $0$.
$A = \{1,2,3,4,5,6,....\}$
$B = \{-1,-2-3,-4,-5,-6,.....\}$
Here, there is no common element in the Sets $A$ and $B$. So, the Sets $A$ and $B$ are disjoint Sets.
8. Power Set: The set of all possible subsets of a set is called a power set. The power set always contains $2^n$ elements, where $n$ is the number of elements in the original set.
e.g. Let $A = {1,2,3}$
The number of elements in the power set is $2^n = 2^3 = 8.$
The power set of $A$, $P(A)$ is $\{\phi, \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}\}$
9. Universal Set: A set that contains all related Sets in a given context is called the Universal Set. The universal set is usually denoted by $U$ while all its subsets are denoted by the letters $\mathrm{A}, \mathrm{B}, \mathrm{C}$, etc.
e.g. Let $A$ be the set of all natural numbers and $B$ be the set of integers greater than $-10$ and less than $5$.
$A = \{1,2,3,4,5,6,....\}$
$B = \{-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4\}$
The universal Set $U$ may be $\{-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,...\}$ or the set of all integers($Z$) or any larger set containing all the elements of the sub-sets.
Operations on Sets
The operations valid on Sets are:
1. Union: Union of two sets combines the values in both Sets without repetition to form a set. The symbol ' $\cup$ ' is used to denote the union.
Eg. $A = \{1,2,4,5,7,8,9\} , B = \{9,7,21,34\}$
Then union of Sets $A$ and $B$, $A \cup B = \{1,2,4,5,8,9,7,21,34\}$
2. Intersection: Intersection of two Sets is a set containing the common elements of both Sets. The symbol ' $\cap U$ ' is used to denote the intersection.
Eg. $A = \{1,2,4,5,7,8,9\} , B = \{9,7,21,34\}$
Then intersection of Sets $A$ and $B$, $A \cap U B = \{7,9\}$
3. Complement: Let $U$ be the universal set and $A$ is a subset of $U$. Then the complement of $A$ is the set of all elements of $U$ which are not the elements of $A$. Symbolically, we use $A^{\prime}$ or $A^C$ to denote the complement of $A$ with respect to $U$.
Eg. Let the universal Set $U$ be $\{-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,...\}$
$A = \{1,2,3,4,5,6,....\}$
$A^C = \{-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0\}$
4. Difference: The difference of the Sets $A$ and $B$ in this order is the set of elements that belong to $A$ but not to B. Symbolically, the difference of Sets is denoted by ‘$-$’
For example, If $A=\{1,2,3,4\}$ and $B=\{4,5,6,8\}$,
Then, $A-B=\{1,2,3\}$ and $B-A=\{5,6,8\}$
Important Formulae of Sets
| Formula Type | Formula |
|---|---|
| Union of Two Sets | $A \cup B = {x : x \in A \text{ or } x \in B}$ |
| Intersection of Two Sets | $A \cap B = {x : x \in A \text{ and } x \in B}$ |
| Difference of Two Sets | $A - B = {x : x \in A \text{ and } x \notin B}$ |
| Complement of a set | $A' = {x : x \notin A}$ |
| Number of elements in the union | $n(A \cup B) = n(A) + n(B) - n(A \cap B)$ |
| Number of elements in difference | $n(A - B) = n(A) - n(A \cap B)$ |
| Subset definition | $A \subseteq B \iff \forall x (x \in A \rightarrow x \in B)$ |
| Proper subset definition | $A \subset B \iff A \subseteq B \text{ and } A \neq B$ |
| Power set formula | $n(\mathcal{P}(A)) = 2^{n(A)}$ |
| Cartesian product of Sets | $A \times B = {(a,b) : a \in A \text{ and } b \in B}$ |
| Universal set relation | $A \cup A' = U$ |
| Intersection with complement | $A \cap A' = \emptyset$ |
| De Morgan’s Law 1 | $(A \cup B)' = A' \cap B'$ |
| De Morgan’s Law 2 | $(A \cap B)' = A' \cup B'$ |
Properties of Sets
Here’s a concise table summarising the Properties of Sets with three columns — property name, description, and formula:
| Property Name | Description | Formula |
|---|---|---|
| Commutative Property | The order of Sets doesn’t matter in the union or intersection | $A \cup B = B \cup A$, $A \cap B = B \cap A$ |
| Associative Property | Grouping of Sets doesn’t change the result | $(A \cup B) \cup C = A \cup (B \cup C)$, $(A \cap B) \cap C = A \cap (B \cap C)$ |
| Distributive Property | Union and intersection can be distributed over each other | $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$, $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ |
| Identity Property | Union with the empty set or intersection with the universal set gives the same set | $A \cup \emptyset = A$, $A \cap U = A$ |
| Complement Property | A set and its complement cover all elements or none in common | $A \cup A' = U$, $A \cap A' = \emptyset$ |
| Idempotent Property | Operating twice doesn’t change the set | $A \cup A = A$, $A \cap A = A$ |
| Complement of Special Sets | The universal set and the empty set complement each other | $(U)' = \emptyset$, $(\emptyset)' = U$ |
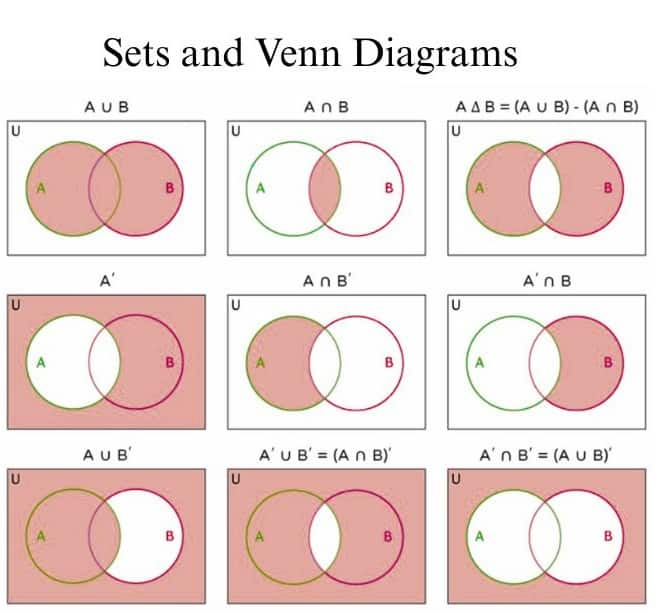
Sets and Venn Diagrams
Venn diagrams are a visual way to represent sets and their relationships, such as union, intersection, and complement. They make it easier to understand how different sets interact and solve problems quickly. The diagram below illustrates these concepts for better clarity.
List of related topics to Sets according to NCERT/JEE Main
This section covers all the important topics from Sets that are based on the NCERT books and are frequently asked in JEE Main exams. It will help you focus on the right areas while studying and ensure you don’t miss any essential concepts needed for better preparation. The list is simple, clear, and aligned with the exam pattern.
Sets in Mathematics: Solved Previous Year Questions
Example 1: Which of the following are equal Sets?
1) $A=\{1,2,3,4\}$ and $B=$ collection of natural numbers less than 6
2) $A=\{$ prime numbers less than 6$\}$ and $B=\{$ prime factors of 30$\}$
3) $A=\{0\}$ and $B=\{x: x>15$ and $x<5\}$
4) $\mathrm{A}=\{5\}$ and $\mathrm{B}=\left\{\mathrm{x}: x^2=25\right\}$
Solution: In option (1), $A=\{1,2,3,4\}$ but $B=\{1,2,3,4,5\}$, hence not equal.
In option (2), $A=\{2,3,5\}$ but $B=\{2,3,5\}$, hence equal.
In option (3), $A=\{0\}$ but $B=$ Null set, hence not equal.
In option (4), $A = {5}$ but $B = {-5, 5}$, hence not equal.
Hence, the answer is option (2).
Example 2: If a set has $32$ subsets. How many elements does it have?
Solution: As we know, if a set has $n$ elements, it will have $2^n$ subsets.
Thus $2^n=32$
$\Rightarrow n=5$
Hence, the answer is $5$.
Example 3: $\mathbf{A}$ is a set containing $\mathbf{n}$ elements. A subset $P_1$ is chosen and $\mathbf{A}$ is reconstructed by replacing the elements of $P_1$. The same process is repeated for sub-sets $P_1, P_2, \ldots, P_m$ with $m>1$. The number of ways of choosing $P_1, P_2, \ldots, P_m$, $P_1 \cup P_2 \cup \ldots \cup P_m=A$ so that $P_1 \cup P_2 \cup \ldots \cup P_m=A$ is
1) $\left(2^m-1\right)^{m n}$
2) $\left(2^n-1\right)^m$
3) ${ }^{m+n} C_m$
4) none of these
Solution:
$\operatorname{Let} A=\left\{a_1, a_2, \ldots, a_n\right\}$ for each $a_i(1 \leq i \leq n)$
Either $a_i \in P_j$ or $a_i \notin P_j(1 \leq j \leq m)$
$\therefore$ There are $2^m$ choices in which $a_i, a_j$ belongs to $P_j$,
Also, there is exactly one choice, i.e, $a_i \notin P_j$
$\therefore a_i \in P_1 \cup P_2 \cup \ldots \cup P_m$ in ( $2^m-1$ ) ways.
Since there are n elements in the set A, the number of ways of constructing subsets is.
$P_1, P_2, \ldots, P_m$ is $\left(2^m-1\right)^n$
Solution:
$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B)=12+9-4=17 \\ & n(A \cup B)^{\prime}=n(U)-n(A \cup B)=20-17=3 \end{aligned} $
Hence, the answer is 3.
Example 5: If $A-B=X$ and $A-C=Y$. then the simplification of $A-(B \cup C)$ is
1) $X \cap Y$
2) $X \cup Y$
3) $X-Y$
4) $Y-X$
Solution: $P-Q=P \cap Q^{\prime}$
So, $A - (B \cup C) = A \cap (B \cup C)'$
$A \cap (B' \cap C') = (A \cap B') \cap (A \cap C') = (A - B) \cap (A - C)$
$X \cap Y$
Hence, the answer is option 1.
How to Study Sets Effectively?
Sets become easy and interesting when studied systematically. Building strong basics in this chapter is important as it supports many topics in higher classes and competitive exams.
-
Begin with the basics: Clearly understand the definition of a set and learn the standard ways of representing sets (roster form and set-builder form).
-
Learn the types of sets thoroughly: Be clear about different types such as empty set, finite and infinite sets, equal sets, subsets, and universal sets.
-
Practise set operations regularly: Focus on operations like union, intersection, and complement, and use Venn diagrams to visualise concepts.
-
Solve a variety of examples: Work through solved examples first and then attempt questions on your own to strengthen understanding.
-
Prepare smartly for exams: For competitive exams, focus on concept-based practice rather than memorising solutions. A strong foundation will help you solve even tricky problems confidently.
Some Basic Concepts of Sets in Different Exams
The chapter on Sets forms a fundamental part of mathematics and is frequently asked in school exams, competitive exams, and entrance tests. The table below provides a clear overview of focus areas, commonly asked topics, and preparation tips for each exam to help you study effectively.
| Exam Name | Focus Area | Common Topics Asked | Preparation Tips |
|---|---|---|---|
| CBSE Board | Conceptual clarity & numericals | Definitions of sets, types of sets, set operations, and Venn diagrams | Read NCERT thoroughly + solve all examples and exercises |
| JEE Main | Problem-solving & accuracy | Union, intersection, complement, Venn diagram-based problems | Practice a variety of numerical-based questions and MCQs |
| JEE Advanced | Analytical thinking | Complex Venn diagram problems, set identities, proofs | Solve previous years’ advanced problems and tricky set questions |
| NEET | Basics & speed | Simple set operations, Venn diagrams | Focus on quick problem-solving and formula applications |
| State Board Exams | Theory-oriented | Definitions, types of sets, basic operations | Revise textbook examples and solve all in-chapter exercises |
| Mathematics Olympiads | Concept application | Advanced set problems, combinations using sets, Venn diagrams | Strengthen fundamentals and practice creative problem-solving |
Recommended Books for Sets
This section lists the best books for studying Sets, with clear explanations and plenty of practice questions. These books will help you strengthen your concepts and prepare effectively for exams.
| Book Name | Why It’s Helpful |
|---|---|
| NCERT Class 11 | Clear and simple explanations. Helps in understanding the representation of Sets and basic definitions. |
| Algebra by Arihant (Dr SK Goyal) | Detailed explanations and plenty of Sets of math examples with answers for practice. |
| RD Sharma Mathematics | Step-by-step problems with conceptual clarity and extra exercises. |
| Cengage Mathematics Algebra | Good for advanced practice and strengthening problem-solving techniques. |
Note: Start with NCERT and then choose one of the other books based on your level and comfort. It’s better to follow one reference thoroughly than to switch between multiple books.
NCERT Resources for Sets
This section offers comprehensive NCERT resources for Sets, including clear explanations and ample practice problems. It helps students strengthen their fundamentals, clear basic concepts, and gain confidence in solving questions from this chapter.
NCERT Subject-Wise Resources
This section provides subject-wise NCERT resources such as NCERT notes and solutions to help you study and practice effectively.
| Resource | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT Notes Class 11 Maths | NCERT Notes Class 11 Physics | NCERT Notes Class 11 Chemistry |
| NCERT Solutions | NCERT Solutions for Class 11 Mathematics | NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Practice Questions on Sets
This section contains a wide range of practice questions designed to help you apply the concepts of Sets effectively. Regular practice will strengthen your problem-solving skills, improve conceptual clarity, and prepare you for school exams as well as competitive exams like JEE Main.
Conclusion
Sets form the backbone of modern mathematics and are used across many chapters and applications. A clear understanding of definitions, symbols, and operations helps in solving problems accurately. With regular practice and concept-based learning, students can master this chapter and build a strong base for advanced topics.
Frequently Asked Questions (FAQs)
A set is a collection of well-defined objects or elements grouped together based on a common property. These objects can be numbers, letters, or anything else that can be clearly identified.
The symbol $\cap$ represents the intersection of two sets, which includes only the elements that are present in both sets.
The symbol $\cup$ represents the union of two sets, which includes all elements from both sets without repeating them.
The symbol $\emptyset$ or ∅ is called the empty set. It is a set that does not contain any elements.
No, union and intersection are not opposites. Union combines all elements from two sets, while intersection only includes elements that are common to both sets. They are different operations but often used together in problems.
$Z$ represents the set of all integers.
Set Symbol | Meaning |
|---|---|
$\{\}$ | symbol of set |
$U$ | universal set |
$n(X)$ | cardinal number of set |
$b ∈ A$ | $b$ is element of $A$ |
$a ∉ B$ | $a$ is not element of $B$ |
$∅$ | null set |
$A U B$ | union of $A$ and $B$ |
$A ∩ B$ | intersection of $A$ and $B$ |
$A ⊆ B$ | $A$ is subset of $B$ |
$B ⊇ A$ | set $B$ is superset of $A$ |
Questions related to
On Question asked by student community
You can download all sets of 2025 Economics Question Papers- Download here .
In UP Board (UPMSP) Class 12 exams, the exam authority typically allows one student at one desk. And usually 4 to5 sets of question paper are distributed.
The CBSE Sahodaya Class 10 Pre-Board Exams are conducted by Sahodaya School Clusters. You can access the CBSE Sahodaya Class 10 Pre-Board Question Paper 2025-26 from this link. The answer key for these question papers will be updated in the article soon.
All the Sahodaya Papers with all the sets are mentioned below in the link attached below:
https://school.careers360.com/articles/sahodaya-question-paper-2025
Hi Shiva Pal,
Download the JNVST Class 9 Question papers from the link provided below.
Link: https://school.careers360.com/articles/jnvst-class-9-question-paper

