Chord of Contact and Diameter of Parabola

What is a Chord of Contact?

The chord of contact is the line segment joining the points of contact of two tangents drawn from an external point to a parabola. It plays a key role in understanding tangential properties and geometric constructions related to conic sections.

Meaning and Definition

A chord of contact is a line segment formed by joining the points of tangency of two tangents drawn from an external point to a conic section such as a circle, parabola, ellipse, or hyperbola.

Suppose tangents are drawn from an external point $P(x_1, y_1)$ to a conic. Let the points where these tangents touch the curve be $T_1$ and $T_2$. Then the line segment $T_1T_2$ is called the chord of contact of the point $P$ with respect to the conic. The standard equation of the chord of contact is given by: $T=0$

Here, $T = 0$ represents the tangent form of the equation of the conic, where the coordinates of the external point are substituted into the general equation using the tangent method.

This concept is widely used in coordinate geometry, especially when dealing with tangents from a point to a parabola or circle, and is essential for solving many Class 11 and competitive exam questions.

Geometric Explanation

Geometrically, a chord of contact is the secant line that joins the two points where tangents from an external point touch a conic. For example, in a circle, this chord lies entirely outside the circle and does not intersect it except at the tangency points.

In the case of a parabola, the tangents drawn from an external point (outside the curve) will touch the parabola at two points, and the line connecting these is the chord of contact. This chord intersects the parabola at exactly those two points and helps analyse the reflective property and symmetry of the parabola.

• For a circle with equation $x^2 + y^2 = r^2$, and external point $P(x_1, y_1)$, the chord of contact is:
  $xx_1 + yy_1 = r^2$

• For a parabola with standard form $y^2 = 4ax$, the chord of contact from $P(x_1, y_1)$ is:
  $yy_1 = 2a(x + x_1)$

This use of T = 0 helps to derive the chord directly from the conic’s equation without knowing the exact points of tangency.

Understanding the chord of contact helps in problems involving tangents, normals, and optical properties of parabolas, and also forms a bridge to more complex ideas like the diameter of a parabola.

Chord of Contact of a Parabola

The chord of contact of a parabola is the straight line joining the points where two tangents, drawn from an external point, touch the parabola. It provides a concise way to represent the combined contact points in a single linear equation.

Definition and Concept

In the case of a parabola, the chord of contact is the line that joins the points where two tangents from an external point touch the parabola. If you have an external point $P(x_1, y_1)$ and you draw two tangents to the parabola from that point, the line joining the points of contact of these tangents is known as the chord of contact of the parabola.

This concept is especially important in the study of standard parabolic forms like $y^2 = 4ax$, and it helps in solving many coordinate geometry problems efficiently. The chord of contact gives insight into how external points interact geometrically with the conic, especially in problems involving tangents, normals, and reflective properties.

Chord of Contact of Parabola Formula

For a parabola in standard form:

$y^2 = 4ax$

The chord of contact from an external point $P(x_1, y_1)$ is given by the equation:

$yy_1 = 2a(x + x_1)$

This formula directly gives the line (chord) joining the points of contact of the tangents drawn from the external point. It eliminates the need to find the actual points of tangency.

If the parabola is of the form $x^2 = 4ay$, then the chord of contact from $P(x_1, y_1)$ is:

$xx_1 = 2a(y + y_1)$

Condition of Chord of Contact – T = 0

The general method to find the chord of contact for any conic (including a parabola) is to use the $T = 0$ condition.

For the parabola $y^2 = 4ax$, the general expression of $T$ (using point $P(x_1, y_1)$) is:

$T = yy_1 - 2a(x + x_1)$

So, the chord of contact is found by setting:

$T = 0 \Rightarrow yy_1 = 2a(x + x_1)$

This condition simplifies finding the equation of the chord of contact without explicitly computing the tangents.

Example: Find the equation of the chord of contact of the tangents drawn from the point $P(3, 4)$ to the parabola $y^2 = 8x$.

Solution:

Here, the parabola is $y^2 = 4a x$, so we compare:

$4a = 8 \Rightarrow a = 2$

Using the chord of contact formula:

$yy_1 = 2a(x + x_1)$

Substitute $x_1 = 3$, $y_1 = 4$, and $a = 2$:

$y \cdot 4 = 2 \cdot 2 (x + 3) \\ 4y = 4(x + 3) \\ 4y = 4x + 12 \Rightarrow y = x + 3$

The chord of contact is: $y=x+3$

Equation of the Chord of Contact of a Parabola

The equation of the chord of contact of a parabola is a powerful tool that allows you to directly find the line joining the points of tangency from an external point without calculating the tangents themselves.

For a parabola given by the standard equation:

$S = y^2 - 4ax = 0$

and an external point $P(x_1, y_1)$, the chord of contact is found using the T = 0 condition. Substituting the coordinates of the external point into the tangent form, the equation becomes:

$T = 0 \quad \text{or} \quad yy_1 - 2a(x + x_1) = 0$

This gives the equation of the chord of contact:

$yy_1 = 2a(x + x_1)$

This formula allows you to directly write the chord from point $P(x_1, y_1)$ to the parabola $y^2 = 4ax$.

Note: The formula $T = 0$ works not just for this standard form but can also be applied to any general parabola. For example, if you have a parabola in the form $x^2 = 4ay$, the chord of contact from $P(x_1, y_1)$ will be:

$xx_1 = 2a(y + y_1)$

By replacing $x$ or $y$ in the conic equation with the corresponding external point coordinates, the T = 0 method simplifies the process of finding chords of contact across all conic sections.

Diameter of the Parabola

In the geometry of conic sections, particularly the parabola, a special line called the diameter plays a crucial role in understanding the symmetry of chords.

The diameter of a parabola is defined as the locus of the midpoints of a system of parallel chords. That means, if you draw several chords on a parabola that are all parallel to one another, and then mark the midpoint of each chord, the path traced by all those midpoints will form a straight line, this line is the diameter of the parabola.

For the standard parabola:

$y^2 = 4ax$

if you consider a family of chords all having the same slope $m$, then the equation of the diameter that bisects these parallel chords is:

$y = \frac{2a}{m}$

This line is perpendicular to the chords and passes through their midpoints, effectively representing the axis of symmetry for that specific family of chords.

Note: The concept of the diameter of a parabola is different from the focal diameter, which is the length of the chord passing through the focus and perpendicular to the axis.

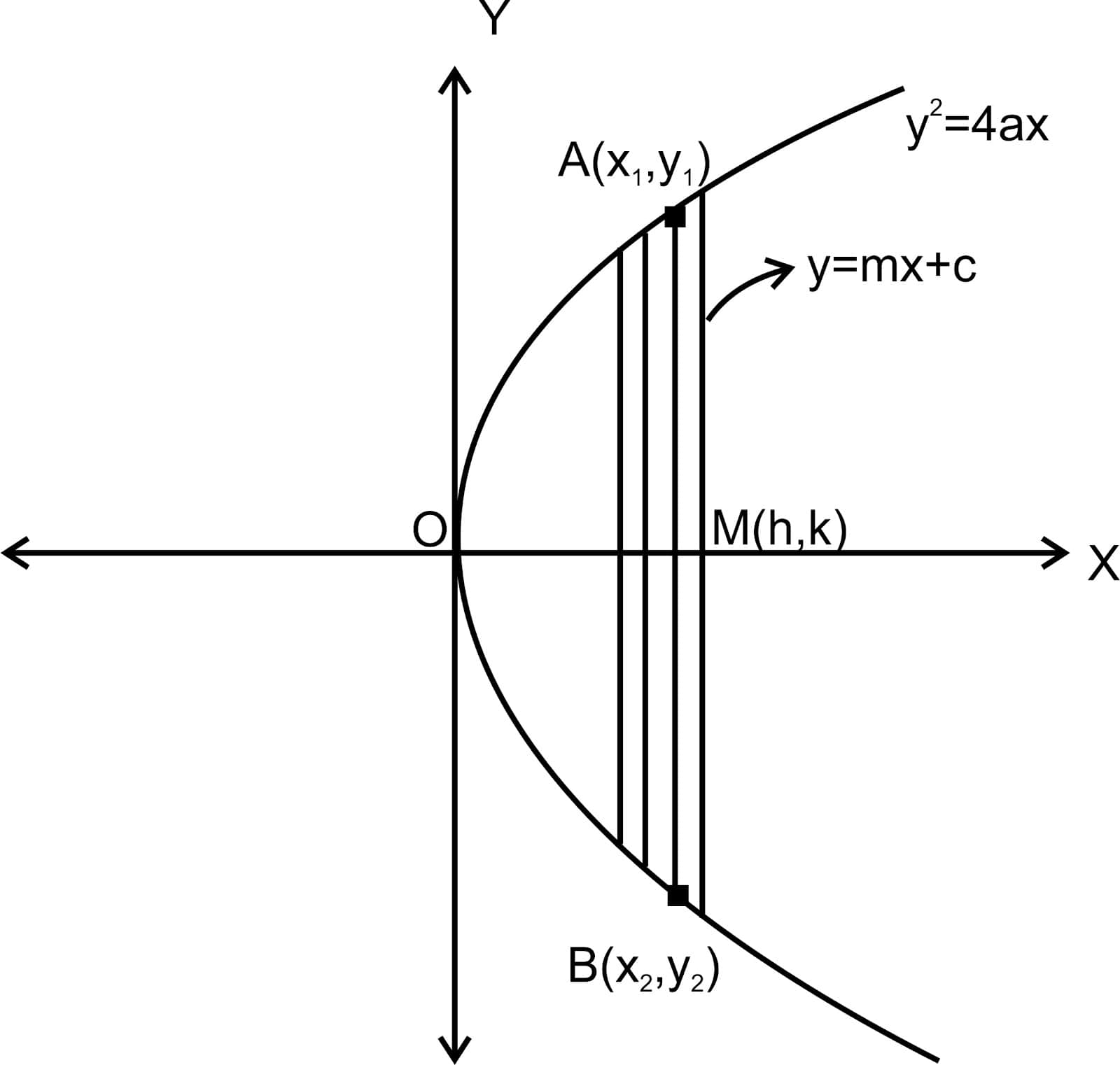
Derivation of the Diameter of a Parabola

To understand the diameter of a parabola, let’s derive its equation using a system of parallel chords.

Consider the standard parabola:

$y^2 = 4ax$

Let there be a system of parallel chords drawn across this parabola, all having the same slope $m$. The general equation of such a family of lines is:

$y=mx+c$

Here, $c$ varies for different chords, but the slope $m$ remains constant. Each unique value of $c$ gives a different chord intersecting the parabola.

Now, let $A(x_1, y_1)$ and $B(x_2, y_2)$ be the endpoints (extremities) of one such chord. Let the midpoint of this chord be $M(h, k)$.

To find the coordinates of $M$, we solve the two equations simultaneously:

$\begin{aligned} & y^2 = 4ax \quad \text{(equation of parabola)} \\ & y = mx + c \quad \text{(equation of chord)} \end{aligned}$

Substitute $y = mx + c$ into the parabola’s equation:

$(mx + c)^2 = 4ax$

Expanding and simplifying:

$m^2x^2 + 2mcx + c^2 = 4ax$

This is a quadratic in $x$, and the sum of roots $x_1 + x_2$ can be found using the relation:

$x_1 + x_2 = \frac{-2mc}{m^2}$

However, we are more interested in the midpoint of the chord, which lies at:

$M(h, k) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$

From the original substitution:

$y = mx + c \Rightarrow y_1 + y_2 = m(x_1 + x_2) + 2c$

Now, solving the parabola and line directly in terms of $y$:

$\begin{aligned} & y^2 = 4a\left(\frac{y - c}{m}\right) \\ \Rightarrow & my^2 - 4ay + 4ac = 0 \end{aligned}$

This is a quadratic in $y$. Using the identity for the sum of roots:

$y_1 + y_2 = \frac{4a}{m}$

Hence, the average (midpoint y-coordinate) is:

$k = \frac{y_1 + y_2}{2} = \frac{2a}{m}$

Since $k$ is the $y$-coordinate of the midpoint $M$, and it's constant for all chords with the same slope $m$, the locus of the midpoint of all such chords is a horizontal line given by:

$y = \frac{2a}{m}$

This is the equation of the diameter of the parabola $y^2 = 4ax$ corresponding to the given slope $m$.

Equation of a Chord Bisected at a given point

In coordinate geometry, another important case arises when you are given the midpoint of a chord of a parabola, and you are asked to find the equation of the chord.

Let’s consider the standard parabola:

$S: y^2 - 4ax = 0$

Let a chord of this parabola have its midpoint at $P(x_1, y_1)$. We want to find the equation of the chord using this information.

The formula used here is based on the idea of T = S₁, where:

• $T$ is the equation obtained by replacing $x$ with $\frac{x + x_1}{2}$ and $y$ with $\frac{y + y_1}{2}$ in the original equation $S$

• $S_1$ is the result of substituting the coordinates of the midpoint $(x_1, y_1)$ directly into the original parabola equation

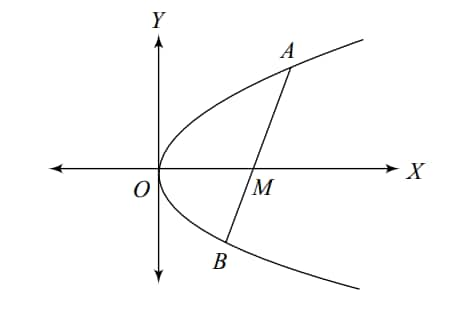
Derivation of the Equation of a Chord Bisected at a Given Point

Let’s derive the equation of a chord of a parabola when the midpoint of the chord is known, a very useful concept in coordinate geometry.

Let the parabola be given by:

$y^2 = 4ax$

Let $AB$ be a chord of the parabola, and let $M(x_1, y_1)$ be the midpoint of this chord.
Assume that the endpoints of the chord are:

• $A \equiv (x_2, y_2)$

• $B \equiv (x_3, y_3)$

Since both points lie on the parabola $y^2 = 4ax$, we have:

$\begin{aligned} & y_2^2 = 4a x_2 \\ & y_3^2 = 4a x_3 \end{aligned}$

Subtracting these two equations:

$y_3^2 - y_2^2 = 4a(x_3 - x_2)$

This can be rearranged using the identity $a^2 - b^2 = (a - b)(a + b)$:

$(y_3 - y_2)(y_3 + y_2) = 4a(x_3 - x_2)$

Dividing both sides by $(x_3 - x_2)$:

$\frac{y_3 - y_2}{x_3 - x_2} = \frac{4a}{y_3 + y_2}$

Since $M(x_1, y_1)$ is the midpoint of $A$ and $B$, we know:

$y_1 = \frac{y_2 + y_3}{2} \Rightarrow y_2 + y_3 = 2y_1$

Substituting:

$\frac{y_3 - y_2}{x_3 - x_2} = \frac{4a}{2y_1} = \frac{2a}{y_1}$

So, the slope of chord AB is:

$\text{slope of } AB = \frac{2a}{y_1}$

Now, using the point-slope form of a straight line, the equation of the chord $AB$ with midpoint $M(x_1, y_1)$ is:

$y - y_1 = \frac{2a}{y_1}(x - x_1)$

Multiplying through to eliminate the fraction:

$yy_1 - y_1^2 = 2a x - 2a x_1$

Rearranging:

$yy_1 - 2a(x + x_1) = y_1^2 - 4a x_1$

So, the final equation of the chord becomes:

$yy_1 - 2a(x + x_1) = y_1^2 - 4a x_1$

This is nothing but the identity:

$T = S_1$

Chord of Contact vs Diameter of Parabola

Understanding the distinction between the chord of contact and the diameter of a parabola is crucial in coordinate geometry. While both relate to lines associated with points on or outside the parabola, they serve very different geometric purposes.

Key Differences

• Definition:
  The chord of contact is the line joining the points of contact of two tangents drawn from an external point. The diameter, on the other hand, is the locus of midpoints of a system of parallel chords of the parabola.

• Point of Reference:
  The chord of contact depends on an external point from which tangents are drawn. A diameter is based on the direction of chords and is not tied to a specific external point.

• Equation:
  Chord of contact has the standard form derived from tangent equations using point T (external): $T = 0$.
  The diameter’s equation is obtained from the midpoint condition or using parametric forms.

• Geometric Role:
  The chord of contact connects two real points on the parabola. The diameter serves as an axis of symmetry for chords parallel to a given direction.

• Tangents vs Chords:
  The chord of contact deals with tangents. The diameter is concerned with chords, specifically their midpoints.

• Dependency on Direction:
  A diameter corresponds to all chords parallel to a given direction. A chord of contact is not direction-based but point-dependent.

• Visual Interpretation:
  The chord of contact lies entirely outside the parabola (except at contact points). Diameters often lie within the parabola’s span, connecting internal midpoints.

Solved Examples Based on the Chord of Contact and Diameter of the Parabola

Example 1: The length of the chord of the parabola $x^2=4 y$ having the equation $x-\sqrt{2} y+4 \sqrt{2}=0$ is: [JEE MAINS 2019]
Solution: Equation of parabola $x^2=4 a y$ and chord $x-\sqrt{2} y+4 \sqrt{2}=0$
Solve these two equations:

$x^2 = 4\left(\frac{x + 4\sqrt{2}}{\sqrt{2}}\right)$

$\Rightarrow \sqrt{2} x^2 = 4x + 16\sqrt{2}$

$\Rightarrow x_1 + x_2 = 2\sqrt{2},\quad x_1 x_2 = -16$

$(\sqrt{2}y - 4\sqrt{2})^2 = 4y$

$\Rightarrow 2y^2 - 20y + 32 = 0$

$\Rightarrow y_1 + y_2 = 10,\quad y_1 y_2 = 16$

Length of chord: $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$

$= \sqrt{(2\sqrt{2})^2 + 64 + 10^2 - 4(16)}$

$= \sqrt{108}$

$= 6\sqrt{3}$

Hence, the answer is $6\sqrt{3}$

Example 2: Let $P Q$ be a focal chord of the parabola $y^2=36 x$ of length 100, making an acute angle with the positive $x$-axis. Let the ordinate of $P$ be positive and $M$ be the point on the line segment PQ such that $\mathrm{PM}: \mathrm{MQ}=3: 1$. Then which of the following points does NOT lie on the line passing through $M$ and perpendicular to the line PQ? [JEE MAINS 2023]
Solution:

$9\left(t + \frac{1}{t}\right)^2 = 100$

$\Rightarrow t = 3$

$\Rightarrow P(81, 54)\ \&\ Q(1, -6)$

$M = (21, 9)$

$\Rightarrow \text{Line } L: (y - 9) = \frac{-4}{3}(x - 21)$

$\Rightarrow 3y - 27 = -4x + 84$

$\Rightarrow 4x + 3y = 111$

Hence, the answer is $(-3,\ 43)$

Example 3: Tangents drawn from the point $(-8,0)$ to the parabola $y^2=8 x$ touch the parabola at $P$ and $Q$. If $F$ is the focus of the parabola, then the area of the triangle $P F Q$ (in sq. units) is equal to :

Solution: We know that,
Standard equation of parabola $-y^2=4 a x$
The equation of $C O C P Q$ is $T=0$
$T \equiv 4\left(x+x_1\right)-y y_1=0$
Where $\left(x_1, y_1\right)$ is $(-8,0)$
The chord of contact is $x=8$
$P(8,8)$ and $Q(8,-8)$
focus $=(2,0)$
$\triangle P Q F=\frac{1}{2}(8-2) \times(8+8)=48$ sq units.

Hence, the answer is 48 sq. units.

Example 4: If two distinct chords of a parabola $y^2=4 a x$, passing through $(a, 2 a)$ are bisected on the line $x+y=1$, then the length of the latus rectum can be less than
Solution: Any point on the line $x+y=1$ can be taken $(t, 1-t)$ equation of the chord, with this as the midpoint

$y(1-t)-2 a(x+t)=(1-t)^2-4 a t$ it passes through $(a, 2 a)$

So, $t^2-2 t+2 a^2-2 a+1=0$, this should have two distinct real roots

$\implies a^2-a<0,0<a<1$.

So, the length of the latus rectum < 4.
Hence, the answer is 4

Example 5: The point $(1,2)$ is one extremity of the focal chord of the parabola $y^2=4 x$. The length of this focal chord is

Solution: The parabola $y^2=4 x$. Here $\mathrm{a}=1$ and focus is $(1,0)$.
The focal chord is ASB. This is clearly the latus rectum of the parabola, and its value = 4.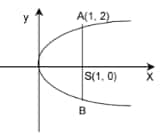

Hence, the correct answer is 4.

List of Topics related to the Chord of Contact

To fully understand the chord of contact in a parabola, it helps to explore related concepts such as tangents, normals, chords, and key properties of the parabola. This section covers important formulas and geometric ideas that connect with the chord of contact and strengthen your overall understanding of parabola-based problems.

• Equations of Normal to a Parabola

• Normal at t1 meets the parabola again at t2

• Length of Tangent, Subtangent, Normal and Subnormal of Parabola

• Properties of Parabola

• Parabola

NCERT Resources

Strengthen your understanding of Class 11 Conic Sections with well-organised NCERT materials. This section includes detailed notes, step-by-step solutions, and exemplar problems to help you master concepts related to parabolas, ellipses, hyperbolas, and circles with clarity and confidence.

NCERT Notes for Class 11 Maths Chapter 11 - Conic Sections

NCERT Solutions for Class 11 Maths Chapter 11 - Conic Sections

NCERT Exemplar Solutions for Class 11 Maths Chapter 11 - Conic Sections

Practice Questions based on the Chord of Contact

Test your understanding of parabolas, circles, and their properties with these carefully curated MCQs. These practice problems cover key concepts like chord of contact, diameter of a parabola, radical axis, and intersection of conics, ideal for board exams and competitive preparation.

Chord Of Contact And Diameter Of Parabola - Practice Question MCQ

You can practice the following topics of conic sections: