Circumcircle of a Triangle

A triangle is a polygon with 3 sides. A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. A triangle has six main elements, three sides, and three angles. A circumcircle is a circle formed using the vertices of the triangle. In real life, we use circumcircle in coastal navigation. It is also a way of obtaining a position line using a sextant when no compass is available.

This Story also Contains

1. What is the Circumcircle of a Triangle?
2. Circumcenter Formula
3. Radius of Circumcircle
4. Derivation of Radius of Circumcircle
5. Formulas to Locate the Circumcenter of Triangle
6. Relation between circumradius and Area of triangle
7. Properties of Circumcenter
8. Solved Examples Based on Circumcircle

In this article, we will cover the concept of the Circumcircle. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of six questions have been asked on this concept including one in 2021.

What is the Circumcircle of a Triangle?

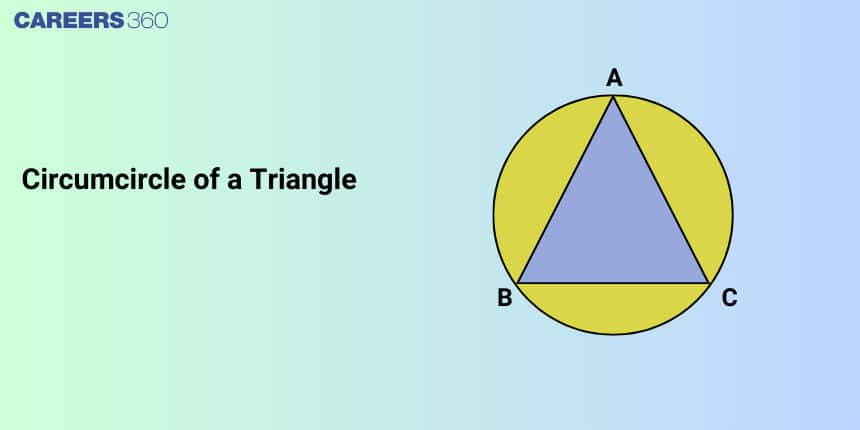
The circumcircle of triangle $A B C$ is the unique circle passing through the three vertices $A, B,$ and $C$. Its center, the circumcenter $O$, is the intersection of the perpendicular bisectors of the three sides. The circumradius is always denoted by $R$.

Circumcenter Formula

$\mathrm{P}(\mathrm{X}, \mathrm{Y})=\left(\frac{x_1 \sin 2 A+x_2 \sin 2 B+x_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}, \frac{y_1 \sin 2 A+y_2 \sin 2 B+y_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}\right)$

Radius of Circumcircle

The radius of the circumcircle of a $ΔABC, R$ is given by the law of sines:

$\mathrm{R}=\frac{a}{2 \sin \mathrm{A}}=\frac{b}{2 \sin \mathrm{B}}=\frac{c}{2 \sin \mathrm{C}}$

Where $a, b, c$ is the side length of a triangle.

Derivation of Radius of Circumcircle

The perpendicular bisector of the sides $A B, B C$, and $C A$ intersects at point $O$. So, $O$ is the circumcentre and

$
O A=O B=O C=R
$
Let $D$ be the midpoint of $B C$.

$
\begin{aligned}
& \angle B O C=2 \angle B A C=2 A \\
& \angle B O D=\angle C O D=A
\end{aligned}
$
So, in $\triangle \mathrm{OBD}$,

$
\begin{aligned}
& \sin \mathrm{A}=\frac{\mathrm{BD}}{\mathrm{OB}}=\frac{a / 2}{\mathrm{R}}=\frac{a}{2 \mathrm{R}} \\
& \Rightarrow \mathrm{R}=\frac{a}{2 \sin \mathrm{A}}
\end{aligned}
$

similarly,

$
\mathrm{R}=\frac{b}{2 \sin \mathrm{B}} \text { and } \mathrm{R}=\frac{c}{2 \sin \mathrm{C}}
$
R can also be written in terms of the area of the triangle

How to Construct Circumcenter of a Triangle?

The circumcenter of any triangle can be constructed by drawing the perpendicular bisector of any of the two sides of that triangle. The steps to construct the circumcenter are:

• Step 1: Draw the perpendicular bisector of any two sides of the given triangle.
• Step 2: Using a ruler, extend the perpendicular bisectors until they intersect each other.
• Step 3: Mark the intersecting point as P which will be the circumcenter of the triangle. It should be noted that, even the bisector of the third side will also intersect at P.

Method to Calculate the Circumcenter of a Triangle

Steps to find the circumcenter of a triangle are:

• Calculate the midpoint of given coordinates, i.e. midpoints of AB, AC, and BC
• Calculate the slope of the particular line.
• By using the midpoint and the slope, find out the equation of the line (y-y₁) = m (x-x₁).
• Find out the equation of the other line in a similar manner.
• Solve two bisector equations by finding out the intersection point.
• Calculated intersection point will be the circumcenter of the given triangle.

Formulas to Locate the Circumcenter of Triangle

Midpoint Formula

Step 1: Calculate the midpoints of the line segments AB, AC, and BC using the midpoint formula.

$M(x, y)=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$

Step 2: Calculate the slope of any of the line segments AB, AC, and BC.

Step 3: Find out the equation of the perpendicular bisector line.

$\left(y-y_1\right)=(-1 / m)\left(x-x_1\right)$

Step 4: Find out the equation of the other perpendicular bisector line.

Step 5: Solve two perpendicular bisector equations to find out the intersection point.

This intersection point will be the circumcenter of the given triangle.

Distance Formula

$d=\sqrt{\left(x-x_1\right)^2+\left(y-y_1\right)^2}$

Step 1 : Find d1,d2 and d3d1,d2 and d3

$d_1=\sqrt{\left(x-x_1\right)^2+\left(y-y_1\right)^2}$ is the distance between circumcenter and vertex AA.

$d_2=\sqrt{\left(x-x_2\right)^2+\left(y-y_2\right)^2}$ is the distance between circumcenter and vertex BB.

$d_3=\sqrt{\left(x-x_3\right)^2+\left(y-y_3\right)^2}$ is the distance between circumcenter and vertex CC.

Extended Sin Law

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2 R$

Given that a, b, and c are lengths of the corresponding sides of the triangle and R is the radius of the circumcircle.

Circumcenter Formula

$O(x, y)=\left(\frac{x_1 \sin 2 A+x_2 \sin 2 B+x_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}, \frac{y_1 \sin 2 A+y_2 \sin 2 B+y_3 \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}\right)$

Relation between circumradius and Area of triangle

Area of $ΔABC,$

$
\begin{aligned}
& \Delta=\frac{1}{2} b \cdot \mathrm{c} \sin \mathrm{A} \\
& \Rightarrow \sin \mathrm{A}=\frac{2 \Delta}{b c}
\end{aligned}
$

and, $\mathrm{R}=\frac{a}{2 \sin \mathrm{A}}$
From (i) and (ii)

$
\mathrm{R}=\frac{a b c}{4 \Delta}
$

Note:

1) The circumcentre of the Acute angled triangle lies inside the triangle.

2) The circumcentre of the obtuse-angled triangle lies outside the triangle.

3) The circumcentre of the right angle triangle is the mid-point of its hypotenuse.

Properties of Circumcenter

Some of the properties of a triangle’s circumcenter are as follows:

• The circumcenter is the centre of the circumcircle
• All the vertices of a triangle are equidistant from the circumcenter
• In an acute-angled triangle, circumcenter lies inside the triangle
• In an obtuse-angled triangle, it lies outside of the triangle
• Circumcenter lies at the midpoint of the hypotenuse side of a right-angled triangle

Recommended Video Based on Circumcircle

Solved Examples Based on Circumcircle

Example 1: Let the centroid of an equilateral triangle $ABC$ be at the origin. Let one of the sides of the equilateral triangle be along the straight line $x + y =3$. If $R$ and $r$ be the radius of the circumcircle and incircle respectively of $\triangle A B C$ then $(R+r)$ is equal to [JEE MAINS 2021]

Solution

$\begin{aligned}
& \mathrm{r}=\mathrm{OM}=\frac{3}{\sqrt{2}} \\
& \sin 30^{\circ}=\frac{1}{2}=\frac{\mathrm{r}}{\mathrm{R}} \\
& \Rightarrow \mathrm{R}=\frac{6}{\sqrt{2}} \\
& \therefore \mathrm{r}+\mathrm{R}=\frac{9}{\sqrt{2}}
\end{aligned}
$

Hence, the answer is $\frac{9}{\sqrt{2}}$

Example 2: If the area of a triangle is $1$ and the products of sides $abc = 8$, then the radius of its circumcircle is.

Solution: We know that,

$\begin{aligned} & R=\frac{a b c}{4 \Delta} \\ & \mathrm{R}=\frac{8}{4.1}=2\end{aligned}$

Hence, the answer is $2$.

Example 3: In triangle ABC, a,b, and c are in G.P., b=2, and the radius of the circumcircle of this triangle is R=1 then find the area of triangle ABC.

Solution: We know that

$
\begin{aligned}
& \Delta=\frac{a b c}{4 R} \\
& \text { Also } a, b, c \text { in } G \cdot P . \Rightarrow b^2=a c
\end{aligned}
$

and $R=1$
So,

$
\Delta=\frac{a c b}{4.1}=\frac{b^3}{4}=\frac{8}{4}=2
$

Hence, the answer is $2$

Example 4: $\ln \Delta \mathrm{ABC}$, let $A D$ be the median and $O, G$, and $P$ be respectively the circumcentre, centroid, and orthocentre. Then $\triangle O G D$ is directly similar to

Solution

Trigonometric Ratios of Functions

$\begin{aligned} & \cos \theta=\frac{\text { Base }}{H y p} \\ & \tan \theta=\frac{O p p}{\text { Base }}\end{aligned}$

From the figure, we can observe that $\Delta O G D$ is directly similar to $\Delta P G A$
Hence, the answer is $\triangle \mathrm{PGA}$

Example 5: Let $(5, \mathrm{a} / 4)$ be the circumcenter of a triangle with vertices $\mathrm{A}(\mathrm{a},-2), \mathrm{B}(\mathrm{a}, 6)$ and $\mathrm{C}(\mathrm{a} / 4,-2)$. Let $\alpha$ denote the circumradius, $\beta$ denote the area, and $\gamma$ denote the perimeter of the triangle. Then $\alpha+\beta+\gamma$ is

Solution: $D$ is the midpoint of $A B . A B$ is perpendicular to $P D$

$
2=\mathrm{a} / 4 \Rightarrow \mathrm{a}=8
$

$\begin{aligned} & \mathrm{A}(8,-2), \mathrm{B}(8,6), \mathrm{C}(2,-2), \mathrm{P}(5,2) \\ & \alpha=\mathrm{AP}=\sqrt{9+16}=5 \\ & \mathrm{AP}=8, \mathrm{BC}=10, \mathrm{AC}=6 \\ & \text { Area }=\beta=(1 / 2) \times 8 \times 6=24 \\ & \text { Perimeter }=\gamma=24 \\ & \alpha+\beta+\gamma=5+24+24=53\end{aligned}$

Hence, the answer is $53.$