Common Chord of two Circles: Equation, Properties, Formula

Struggling to find the solution to this math question involving circles? Wondering how to solve this question step by step when two circles intersect? If you're looking for the answer to this question or need a clear question and solution example with proper reasoning, you're in the right place. Understanding the common chord of two circles is essential for mastering coordinate geometry and circle-based problems in mathematics. Here, you'll get the solution of the given question, including the question's answer with explanation and a detailed solution of this question that breaks down each concept simply. In this article, we’ll explore how to find the common chord of two circles with a complete step-by-step method and solved examples.

Common Chord of Two Circles

A circle is defined as the set (or locus) of all points in a plane that are at a constant distance from a fixed point. This fixed point is called the centre of the circle, usually denoted by $O$, and the constant distance is called the radius, denoted by $r$.

When two circles intersect, they do so at two distinct points (provided they are not tangent). The straight line that passes through both of these points of intersection is called the common chord of the two circles. In coordinate geometry, this chord represents the set of all points that lie on both circles simultaneously. Mathematically, if the two circles are represented by their equations, the equation of the common chord can be found by subtracting the two equations, which eliminates the squared terms.

Suppose the equations of the two circles are:
$S_1: x^2 + y^2 + 2g_1x + 2f_1y + c_1 = 0$
$S_2: x^2 + y^2 + 2g_2x + 2f_2y + c_2 = 0$

Subtracting $S_2$ from $S_1$ gives the equation of the common chord:
$2(g_1 - g_2)x + 2(f_1 - f_2)y + (c_1 - c_2) = 0$

This linear equation represents the common chord, a straight line that cuts both circles at the same two points.

Equation of a circle

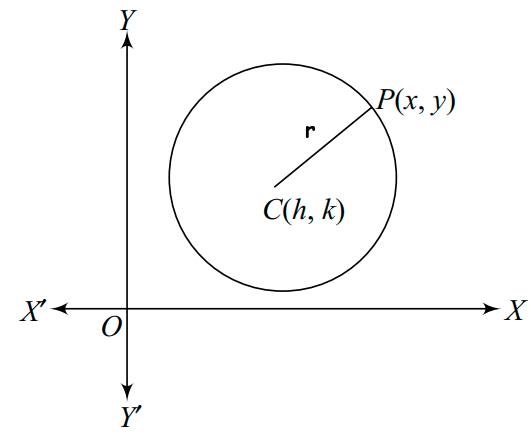
Using the distance formula, the equation of a circle with centre at $C(h, k)$ and radius $r$ can be derived as:

$\sqrt{(x - h)^2 + (y - k)^2} = r$

Squaring both sides to eliminate the square root:

$(x - h)^2 + (y - k)^2 = r^2$

This is the standard form of the equation of a circle in coordinate geometry.

If the centre of the circle is at the origin, i.e., $(0, 0)$, then the equation simplifies as follows:

$(x - 0)^2 + (y - 0)^2 = r^2 \Rightarrow x^2 + y^2 = r^2$

This is the equation of a circle centred at the origin with radius $r$.

Geometric Interpretation of the Common Chord Between Two Circles

When two circles intersect at exactly two points, say points $A$ and $B$, the straight line that connects these two points is known as the common chord of the circles. This line lies on both circles and represents the set of all points that satisfy both circle equations simultaneously.

Suppose the equations of the two intersecting circles are:

$S = x^2 + y^2 + 2gx + 2fy + c = 0$

$S' = x^2 + y^2 + 2g'x + 2f'y + c' = 0$

To find the equation of the common chord, we subtract $S'$ from $S$, eliminating the $x^2$ and $y^2$ terms:

$S - S' = 2x(g - g') + 2y(f - f') + (c - c') = 0$

This linear equation represents the common chord, a straight line that cuts through the points of intersection of both circles.

Alternatively, we can simply write:

$S−S′=0$

This gives a quick and direct method to find the equation of the common chord if both circle equations are known.

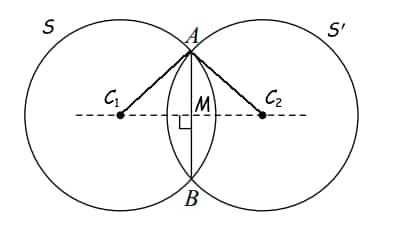
Length of the Common Chord AB

The length of the common chord, denoted by $AB$, can be calculated geometrically using the Pythagorean Theorem. Let $C_1$ be the centre of the first circle ($S = 0$), and let $M$ be the midpoint of chord $AB$ (which lies on the line joining the centres and is perpendicular to the chord). Then:

$AB = 2 \times AM$

Using the right triangle $\triangle C_1AM$, we apply:

$AB = 2\sqrt{(C_1A)^2 - (C_1M)^2}$

Where:

• $C_1A$ is the radius of the first circle, calculated as
  $C_1A = \sqrt{g^2 + f^2 - c}$

• $C_1M$ is the perpendicular distance from the centre $C_1$ to the common chord (i.e., length of the altitude from $C_1$ to line $AB$)

This geometric relationship helps visualise how the location of the chord and the radius affect its length.

Note: The maximum length of the common chord occurs when the chord becomes the diameter of the smaller circle. In this case, the chord passes through the centre of that circle and is as long as possible within its boundary.

How to Find the Common Chord Equation?

To determine the equation of the common chord of two intersecting circles, we follow a structured approach using coordinate geometry. The key idea is that any point lying on the common chord must satisfy both circle equations simultaneously. Here's how to solve this question step by step:

Step 1: Write the Equations of the Two Circles

Begin with the general form of the equations of two circles:

$S_1: x^2 + y^2 + 2g_1x + 2f_1y + c_1 = 0$

$S_2: x^2 + y^2 + 2g_2x + 2f_2y + c_2 = 0$

These represent two circles with centres at $(-g_1, -f_1)$ and $(-g_2, -f_2)$ and respective radii that can be derived from the standard circle formula.

Step 2: Subtract the Equations to Get the Chord Equation

To eliminate the common quadratic terms ($x^2$ and $y^2$), subtract $S_2$ from $S_1$:

$(S_1 - S_2):\ (2g_1 - 2g_2)x + (2f_1 - 2f_2)y + (c_1 - c_2) = 0$

Simplify the expression:

$2(g_1 - g_2)x + 2(f_1 - f_2)y + (c_1 - c_2) = 0$

This is the equation of the common chord, a straight line passing through the points of intersection of the two circles.

Step 3: Find the Points of Intersection

In many problems, especially in coordinate geometry or conic sections, you may be asked to find the points where the two circles intersect. This can be done by solving the two circle equations simultaneously, often by substituting one into the other.

These points lie on both circles and also on the chord you just found. Finding them can help verify or graphically understand the solution.

Step 4: Final Form of the Common Chord Equation

Once simplified, the final form of the common chord is a linear equation:

$Ax+By+C=0$

Where:

• $A = 2(g_1 - g_2)$

• $B = 2(f_1 - f_2)$

• $C = c_1 - c_2$

This line is perpendicular to the line joining the centres of the two circles and passes through the points where the circles intersect.

Real-Life Applications and Importance in Geometry

The concept of a common chord is not just theoretical; it has practical importance in various fields:

• Engineering and Design: When designing mechanical parts with circular components, understanding the geometry of intersecting circles helps ensure precise fitting.

• Astronomy and Physics: Common chords are used in calculating trajectories and angles between circular orbits.

• Navigation and Mapping: In geographical systems, overlapping circular zones (such as signal ranges or coverage areas) use the idea of a common chord to determine shared regions.

• Mathematical Proofs: In coordinate geometry and Euclidean constructions, the common chord plays a crucial role in determining angles, perpendicular bisectors, and symmetry.

Solved Examples Based on the Equation of the Common Chord of Two Circles

Example 1: The common tangent to the circle $x^2+y^2=4$ and $x^2+y^2+6 x+8 y-24=0$ also passes through the point :
1) $(4,-2)$
2) $(-6,4)$
3) $(6,-2)$
4) $(-4,6)$
Solution:

The equation of the common chord of two circles
$(S) = x^2 + y^2 + 2gx + 2fy + c = 0$
$(S') = x^2 + y^2 + 2g'x + 2f'y + c' = 0$

The equation of the common chord is:
$2x(g - g') + 2y(f - f') + (c - c') = 0$
or, $S - S' = 0$

Now consider:
$x^2 + y^2 - 4 = 0$
$x^2 + y^2 + 6x + 8y - 24 = 0$

Subtracting:
$S_2 - S_1 = (x^2 + y^2 + 6x + 8y - 24) - (x^2 + y^2 - 4)$
$= 6x + 8y - 20 = 0$

So, the equation of the common chord is: $3x + 4y = 10$

Hence, point $(6,-2)$ lies on the above line.

Example 2: If the circles $x^2+y^2+5 K x+2 y+K=0$ and $2\left(x^2+y^2\right)+2 K x+3 y-1=0(K \epsilon R)$, intersect at the points P and Q, then the line $4 x+5 y-K=0$ passes through P and Q, for:

1) infinitely many values of $K$
2) no value of $K$
3) exactly two values of $K$
4) exactly one value of $K$

Solution:

Common Chord of Two Circles:

The equation of the common chord of two circles

$S = x^2 + y^2 + 2gx + 2fy + c = 0$

$S' = x^2 + y^2 + 2g'x + 2f'y + c' = 0$

is $2x(g - g') + 2y(f - f') + c - c' = 0$

or, $S - S' = 0$

Given that two circles are

$S_1 = x^2 + y^2 + 5Kx + 2y + K = 0$

$S_2 = 2(x^2 + y^2) + 2Kx + 3y - 1 = 0$

Equation of the common chord

$S_1 - S_2 = 0$

$\Rightarrow 4Kx + \frac{1}{2}y + K + \frac{1}{2} = 0$
Given the equation of the chord is

$4x + 5y - k = 0$

On comparing (1) and (2),

$k = \frac{1}{10} = \frac{k + \frac{1}{2}}{-k}$

There is no value of $k$

So, option (2) is correct.

Example 3: If the angle of intersection at a point where two circles with radii 5 cm and 12 cm intersect is $90^{\circ}$, then the length (in cm ) of their common chord is :

1)$\frac{13}{2}$

2) $\frac{13}{5}$

3) $\frac{120}{13}$

4) $\frac{60}{13}$

Solution:
Length of Common Chord –

$AB = 2(AM) \quad (\because m$ is mid-point of $AB)$

$= 2 \sqrt{(C_1A)^2 - (C_1M)^2}$

$C_1A = $ radius of the circle $S = 0$, i.e., $C_1A = \sqrt{g^2 + f^2 - c}$

$C_1M = $ length of perpendicular from $C_1$ on common chord $AB$

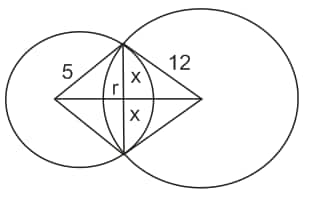
Length of common chord $= 2x$

$\sqrt{s^2 - x^2} + \sqrt{12^2 - x^2} = 13$

$x = \dfrac{12 \times 5}{13}$

$2x = \dfrac{120}{13}$

$x = \dfrac{60}{13}$

Hence, the correct answer is option 4.
Example 4: If the lengths of external and internal common tangents to two circles $\quad x^2+y^2-14 x \quad+4 y-28=0$ are $\lambda$ and $\mu$ the value of $\lambda+\mu$ must be

1) 20

2) 25

3) 18

4) 24

Solution:

The given circles $S_1 \equiv x^2 + y^2 + 14x - 4y + 28 = 0$ and $S_2 \equiv x^2 + y^2 - 14x + 4y - 28 = 0$

Centres and radii of circles $S_1$ and $S_2$ are

$C_1(-7, 2), \quad r_1 = \sqrt{49 + 4 - 28} = 5$

$C_2(7, -2), \quad r_2 = \sqrt{49 + 4 + 28} = 9$ respectively.

Here $d = C_1C_2 = \sqrt{(-7 - 7)^2 + (2 + 2)^2}$

$= \sqrt{212} > r_1 + r_2 = 5 + 9 = 14$

$\therefore d > r_1 + r_2$

Hence, circles don't touch or cut

$\therefore \text{Length of the external common tangent}$

$L_{ex} = \sqrt{d^2 - (r_2 - r_1)^2}$

$= \sqrt{212 - (9 - 5)^2} = \sqrt{212 - 16}$

$= \sqrt{196} = 14 = \lambda$

and the length of the internal common tangent

$L_{in} = \sqrt{d^2 - (r_1 + r_2)^2}$

$= \sqrt{212 - (5 + 9)^2} = \sqrt{212 - 196}$

$= \sqrt{16} = 4 = \mu$

$\therefore \lambda + \mu = 18$

Hence, the answer is option (3).
Example 5: Two circles in the first quadrant of radii $r_1$ and $r_2$ touch the coordinate axes. Each of them cuts off an intercept of 2 units with the line $x+y=2$. Then $r_1^2+r_2^2-r_1 r_2$ is equal to

1) 7

2) 8

3) 6

4) 5

Solution:

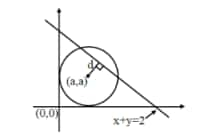
Given: Circle $(x - a)^2 + (y - a)^2 = a^2$

$x^2 + y^2 - 2a x - 2a y + a^2 = 0$

Intercept on line $x + y = 2$ is $2$

$2\sqrt{a^2 - d^2} = 2$

Where $d$ is the perpendicular distance from the centre $(a, a)$ to the line $x + y = 2$

$2\sqrt{a^2 - \left( \dfrac{a + a - 2}{\sqrt{2}} \right)^2} = 2$

$a^2 - \dfrac{(2a - 2)^2}{2} = 1$

$2a^2 - 4a^2 + 8a - 4 = 2$

$2a^2 - 8a + 6 = 0$

$a^2 - 4a + 3 = 0$

$\therefore r_1 + r_2 = 4 \text{ and } r_1 r_2 = 3$

$r_1^2 + r_2^2 - r_1 r_2 = (r_1 + r_2)^2 - 3r_1 r_2$

$= 16 - 9 = 7$

List of topics related to the Common Chord between two circles

Explore key concepts related to the common chord between two circles and its geometric significance. This section covers crucial topics such as the power of a point, chord of contact, director circle, diameter properties, and the angle of intersection, each with definitions, formulas, and derivations to strengthen your understanding of circle geometry.

Power of a point wrt Circle: Meaning, Theorem, Formula

Chord of Contact and Diameter of Parabola

Director Circle: Formula and Equation

Diameter Of A Circle: Definition, Formula, Equation

Angle of Intersection of Two Circles: How to Find, Formula, Derivation

NCERT Resources

Access comprehensive NCERT resources for Class 11 Maths Chapter 10, Conic Sections. This section provides detailed notes, step-by-step solutions, and exemplar problem-solving approaches to help you master the concepts of circles, parabolas, ellipses, and hyperbolas effectively.

NCERT Notes for Class 11 Maths Chapter 10 - Conic Sections

NCERT Solutions for Class 11 Maths Chapter 10 - Conic Sections

NCERT Exemplar Solutions for Class 11 Maths Solutions Chapter 10 - Conic Sections

Practice Questions based on the Common Chord between two circles

Sharpen your understanding of the common chord and related circle concepts with these targeted practice MCQs. Covering topics like chord of contact, director circle, pair of tangents, radical axis, and angle of intersection, these questions are designed to test conceptual clarity and problem-solving speed for competitive exams.

Common Chord Of Two Circles - Practice Question MCQ

You can practice the questions related to the common chord between two circles: