Complement of a set, Law of Complement, Property of Complement

Overview of Sets

Sets are a foundational concept in mathematics, central to various fields such as statistics, geometry, and algebra. A set is simply a collection of distinct objects, considered as a whole. These objects, called elements or members of the set, can be anything: numbers, people, letters, etc. Sets are particularly useful in defining and working with groups of objects that share common properties.

It is a well-defined collection of distinct objects and it is usually denoted by capital letters A, B, C, S, U,V...

Now, let us look into the definition that explain complement of set in detail.

Complement of a Set

The complement of a set is one of the fundamental operations in set theory. It is used to identify elements that do not belong to a specific set when compared with a larger reference set, known as the universal set. This concept is especially useful in problems involving Venn diagrams, logical operations, and data analysis. Before diving into the definition and examples of complement of a set, it's important to understand what sets and universal sets are.

Definition of Complement of a Set

Let $U$ be the universal set and $B$ be a subset of $U$. Then, the complement of set $B$ refers to the set of all elements in $U$ that are not in $B$.

Symbolic Representation: The complement of set $B$ is denoted by $B'$ or $B^C$ (read as "B complement").

$B' = \{x \in U \mid x \notin B\}$

This can also be written as: $B' = U - B$

In simple terms, the complement of a set B includes everything in the universal set except the elements of $B$.

Complement of a Set: Examples

Understanding the complement of a set with examples helps in applying the concept easily to solve problems based on universal sets and subsets. Below are a few solved examples that demonstrate how to find the complement of a set.

Example 1:
Let $U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$ and $A = \{1, 4, 6, 7, 3, 8\}$
Then, the complement of set $A$ is:
$A' = \{2, 5, 9, 10\}$

Example 2:
Let $U = \{\text{blue, violet, green, yellow, grey, brown, black, white, red}\}$
Let $A = \{\text{violet, green, yellow, white}\}$ and $B = \{\text{grey, brown}\}$
Then:
$A' = \{\text{blue, grey, brown, black, red}\}$
$B' = \{\text{blue, violet, green, yellow, black, white, red}\}$

Example 3:
Let $U = \{x \in \mathbb{N} \mid x \leq 10\}$ and $A = \{x \in \mathbb{N} \mid x \leq 5\}$

Now,
$U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$ and $A = \{1, 2, 3, 4, 5\}$
So, $A' = \{6, 7, 8, 9\}$

These examples of complement of a set clearly show how to subtract a subset from its universal set to find the remaining elements.

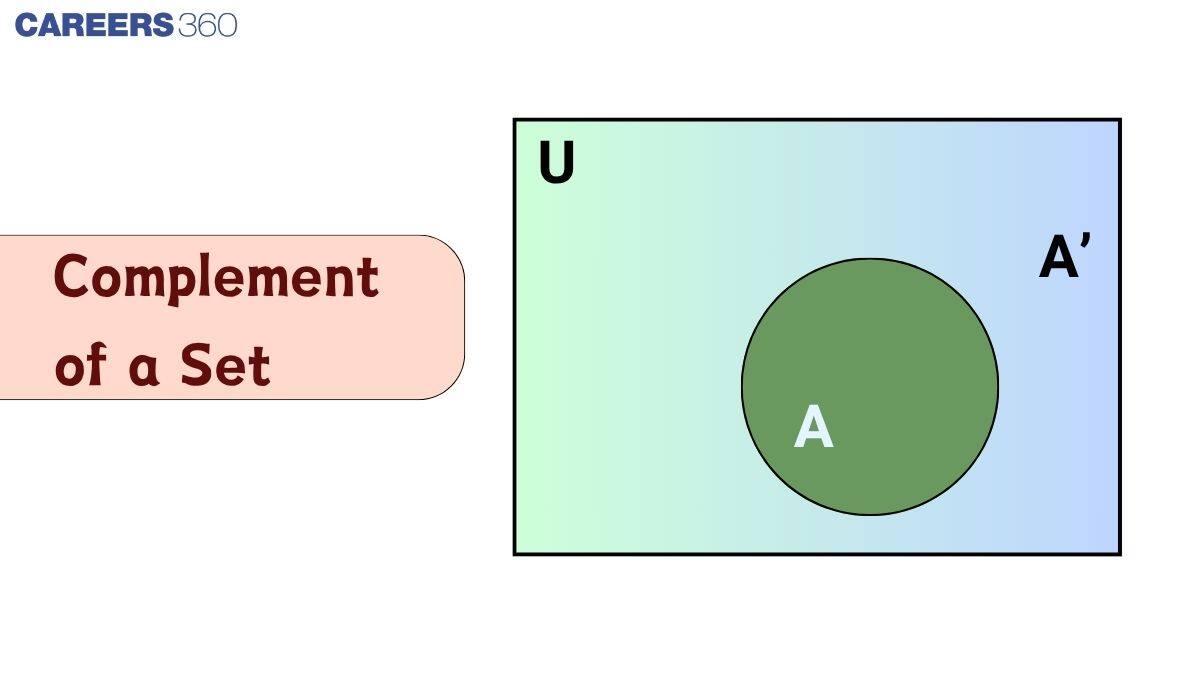
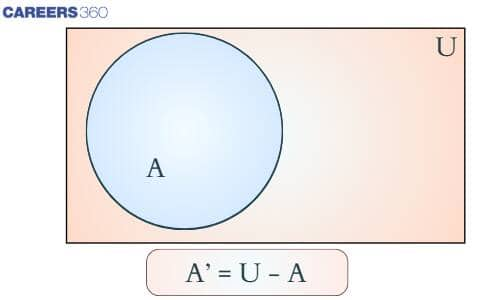
Complement of Set: Venn Diagram

The Venn diagram for the complement of a set helps visualize all elements in the universal set that do not belong to the given set. In a typical Venn diagram, the universal set is represented by a rectangle, and the set in question is shown as a circle within it.

To illustrate the complement of set $A$, we shade the region outside the circle representing $A$, which includes all elements in $U$ that are not in $A$.

This visual representation makes it easier to understand how $A' = U - A$, and is widely used in logic problems and set theory applications.

Laws of the Complement of a Set

The laws of complement of a set are key rules in set theory that describe the relationship between a set, its complement, the universal set, and the empty set. These properties are essential for simplifying set expressions and solving problems involving set operations and Venn diagrams.

Here are the fundamental complement laws in set theory:

1. Complementation Law:
   The complement of the complement of a set returns the original set.
   $\left(A'\right)' = A$
2. Universal Set Complement Law:
   The complement of the universal set is the empty set.
   $U' = \phi$
3. Empty Set Complement Law:
   The complement of the empty set is the universal set. $\phi' = U$

Properties of Complement of Sets

The properties of complement of sets help in understanding how a set behaves with respect to its complement and the universal set. These properties are foundational in set theory, especially in solving problems using Venn diagrams, union, intersection, and De Morgan’s laws. Below are the main properties explained with examples.

1. Complement Laws

• If $A$ is a subset of the universal set $U$, then $A'$ is also a subset of $U$.
• The union of a set and its complement is the universal set: $A \cup A' = U$
• The intersection of a set and its complement is the empty set: $A \cap A' = \emptyset$

Example:
Let $U = \{1, 2, 3, 4, 5\}$ and $A = \{4, 5\}$.
Then, $A' = \{1, 2, 3\}$
Now, $A \cup A' = \{1, 2, 3, 4, 5\} = U$
And, $A \cap A' = \emptyset$

2. Law of Double Complementation

• The complement of the complement of a set gives the original set: $(A')' = A$
• This means if $A'$ is the complement of $A$, then the complement of $A'$ brings us back to $A$.

Example:
Let $U = \{1, 2, 3, 4, 5\}$ and $A = \{4, 5\}$.
Then, $A' = \{1, 2, 3\}$ and $(A')' = \{4, 5\} = A$

3. Law of Empty Set and Universal Set

• The complement of the universal set is the empty set: $U' = \emptyset$
• The complement of the empty set is the universal set: $\emptyset' = U$

Example:
If $U = \{1, 2, 3, 4, 5\}$, then $U' = \emptyset$ and $\emptyset' = \{1, 2, 3, 4, 5\}$

4. De Morgan’s Laws

• The complement of the union of two sets equals the intersection of their complements: $(A \cup B)' = A' \cap B'$
• The complement of the intersection of two sets equals the union of their complements: $(A \cap B)' = A' \cup B'$

These are known as De Morgan’s Laws and are essential in logic and set theory.

Important Notes on the Complement of a Set

• The complement of a set $A$ is denoted as $A'$ and is defined as: $A' = U - A$
• A set and its complement are always disjoint.
• The complement of the universal set is the empty set: $U' = \emptyset$
• The complement of the empty set is the universal set: $\emptyset' = U$

These properties of set complement are frequently applied in mathematical logic, set operations, and Venn diagram-based questions.

Solved Examples Based on the Complement of Set

Example 1: Given $\mathrm{n}(\mathrm{U})=10, \mathrm{n}(\mathrm{A})=5, \mathrm{n}(\mathrm{B})=3$ and $n(A \cap B)=2$. A and B are subsets of $U$, then $n(A \cup B)^{\prime}=$

Solution:
Let $U$ be the universal set and $A$ a subset of $U$. Then the complement of $A$ is the set of all elements of $U$ which are not the elements of A. Symbolically, we write A' to denote the complement of $A$ with respect to $U$.
where $A^{\prime}=\{x: x \in U$ and $x \notin A\}$.Obviously $A^{\prime}=U-A$
$ \begin{aligned} & n(A \cup B)=5+3-2=6 \\ & n(A \cup B)^{\prime}=n(U)-n(A \cup B)=10-6=4 \end{aligned} $
Hence, the answer is 4 .

Example 2: Two newspapers A and B are published in a city. It is known that 25% of the city population reads A and 20% reads B while 8% reads both A and B. Further, 30% of those who read A but not B look into advertisements, and 40% of those who read B but not A also look into advertisements, while 50% of those who read both A and B look into advertisements. then the percentage of the population who look into advertisements is:

Solution:

Let $P(A)$ and $P(B)$ denote respectively the percentage of the city population that reads newspapers $A$ and $B$.

Let us consider the total percentage to be 100 . Then from the given data, we have

$P(A)=25, \quad P(B)=20, P(A \cap B)=8$

$\therefore$ Percentage of those who read $A$ but not $B$

$P(A \cap \bar{B})=P(A)-P(A \cap B)=25-8=17 \%$
And, Percentage of those who read $B$ but not $A$

$P(\bar{A} \cap B)=P(B)-P(A \cap B)=20-8=12 \%$

If $\mathrm{P}(\mathrm{C})$ denotes the percentage of those who look into an advertisement, then from the given data we obtain

$ \begin{aligned} & \therefore P(C)=30 \% \text { of } P(A \cap \bar{B})+40 \% \text { of } P(\bar{A} \cap B)+50 \% \text { of } P(A \cap B) \\ & \Rightarrow P(C)=\frac{3}{10} \times 17+\frac{2}{5} \times 12+\frac{1}{2} \times 8 \\ & \Rightarrow P(C)=13.9 \% \end{aligned} $
Hence, the answer is 13.9%.

Example 3: If $U=\{1,2,3,4,5\}, A=\{3,4,5\}$ and $B=\{1,2\}$. Then which of the following is true, if $U$ is a universal set of $A$ and $B$?
1) $A \subset B$
2) $A=B$
3) $A=B^{\prime}$
4) None of these

Solution:
Clearly B $=\mathrm{U}-\mathrm{A}$
Hence, $B=A^{\prime}$ and $A=B^{\prime}$
Hence, the answer is the option 3.

Example 4: If A and B are such sets that $A \cup B=U$ is the universal set. Which of the following must be true?
1) $A \cap B=\phi$
2) $A \cup B=A \cap B$
3) $A=B^c$
4) $A \cap U=A$

Solution:

$A \cup A^{\prime}=U$
A and B don't need to be compliment sets. It is only possible that
$A \cap U=A$
Hence, the answer is the option 4.

Example 5: If $A \cup B=U$ and $A \cap B=\phi$, then which of the following is not true?
1) $A^{\prime}=B$

2) $A=B^{\prime}$

3) $A \cap B=B \cap A$

4) $A \cup B=A \cap B$

Solution:
Clearly, $A$ and $B$ are complements of each other.
$\mathrm{A}=\mathrm{B}^{\prime}$ and $\mathrm{A}^{\prime}=\mathrm{B}$, so options (1) and (2) are correct.
Now option (3) is always correct as it is the commutative law.
In option (4), $A \cup B=U$ and $A \cap B=\phi$, so they are not equal.
Hence, the answer is the option 4.

List of Topics Related to the Complement of a Set

Explore key concepts that closely relate to the complement of a set, including foundational topics like set notations, subsets, and set operations. Understanding these topics strengthens your grasp of how sets interact within a universal set.

NCERT Resources

Explore essential NCERT resources for Class 11 Sets, including detailed solutions, clear revision notes, and handpicked exemplar problems. These materials are tailored to build a strong foundational understanding and support preparation for both board exams and competitive entrance tests.

NCERT Solutions for Class 11 Chapter 1 Sets

NCERT Notes for Class 11 Chapter 1 Sets

NCERT Exemplar for Class 11 Chapter 1 Sets

Practice Questions on Complement of a Set

Sharpen your understanding of the complement of a set with focused practice questions designed to reinforce key definitions, properties, and formulas. These practice MCQs are ideal for testing your conceptual clarity and preparing for board exams and entrance tests. Explore the links below to attempt topic-wise MCQs and advance your set theory skills systematically.

To practice questions based on Complement Of A Set - Practice Question MCQ, click here.

You can practice the next topics of Sets below: