Composition of function: Conditions and Properties

The composition of functions is a fundamental concept in mathematics where two functions are combined to form a new function. This involves using the output of one function as the input to another function. The composition of functions is denoted by the symbol ∘. It is very important to map two functions in a single function.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Function
2. Composition of function
3. Properties of composition:
4. How to Determine the Composition?
5. Solved Examples Based On the Composition of Functions:

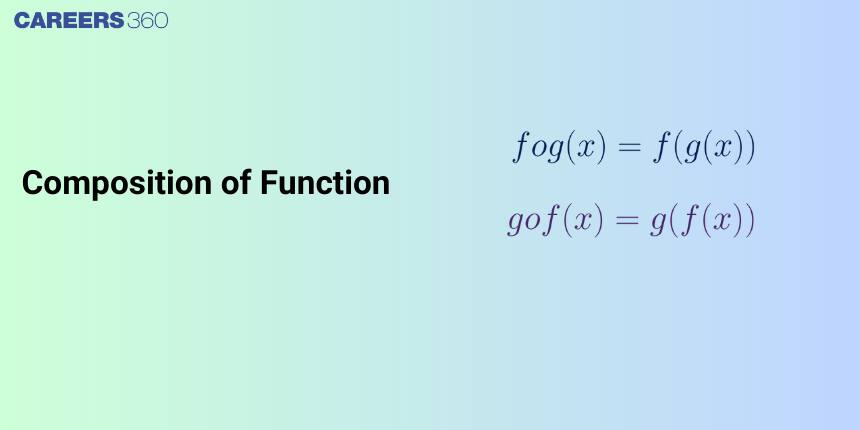
In this article, we will cover the concepts of composition functions. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of twenty-one questions have been asked on this concept, including two in 2016, one in 2017, three in 2019, four in 2020, two in 2021, seven in 2022, and two in 2023.

Function

A relation from a set A to a set B is said to be a function from A to B if every element of set A has one and only one image in set B.

OR

A and B are two non-empty sets, then a relation from A to B is said to be a function if each element x in A is assigned a unique element f(x) in B, and it is written as

f: A ➝ B and read as f is mapping from A to B.

Function

Function

Not a function

Not a function

Third one is not a function because d is not related(mapped) to any element in B.

Fourth is not a function as element a in A is mapped to more than one element in B.

Composition of function

Let f: A $\rightarrow$ B and g: B $\rightarrow$ C be two functions. Then the composition of f and g is denoted by gof and defined as the function gof : A $\rightarrow$ C given by gof (x) = g(f (x))

Symbol of Composition of Functions

The symbol of the composition of functions is ∘. It can also be shown without using this symbol but by using the brackets. i.e.,

• (f ∘ g)(x) = f(g(x)) and is read as "f of g of x". Here, g is the inner function and f is the outer function.
• (g ∘ f)(x) = g(f(x)) and is read as "g of f of x". Here, f is the inner function and g is the outer function.

Properties of composition:

• In general fog ≠ gof (Not commutative)
• fo(goh) = (fog)oh (Associative)
• If f and g are bijections then fog and gof are also bijections
• - The composition of any function with the identity function is the function itself. If $f: A \rightarrow B$, then $f o I_A=I_B \circ f=f$

How to Determine the Composition?

To find the composition $(f \circ g)(x)$

1. Substitute: Substitute the expression for g(x) into the function f.
2. Simplify: Simplify the resulting expression, if necessary.

Finding Composite Function From Graph

To find the composite function of two functions (which are not defined algebraically) shown graphically, we should recall that if (x, y) is a point on a function f(x) then f(x) = y. Using this, to find f(g(a)) (i.e., f(g(x)) at x = a):

• Find g(a) first (i.e., the y-coordinate on the graph of g(x) that corresponds to x = a)
• Find f(g(a)) (i.e., the y-coordinate on the graph of f(x) that corresponds to g(a))

Domain of Composite Functions

In general, if g: X → Y and f: Y → Z then f ∘ g: X → Z. i.e., the domain of f ∘ g is X and its range is Z. But when the functions are defined algebraically, here are the steps to find the domain of the composite function f(g(x)).

• Find the domain of the inner function g(x) (Let this be A)
• Find the domain of the function obtained by finding f(g(x)) (Let it be B)
• Find the intersection of A and B and A ∩ B gives the domain of f(g(x))

Range of Composite Functions

The range of a composite function is calculated just like the range of any other function. It doesn't depend on the inner or outer functions.

Recommended Video Based on Composition of Functions

Solved Examples Based On the Composition of Functions:

Example 1: If $\mathrm{h}(\mathrm{x})=3 \mathrm{x}-5 ; g(x)=2 x^2-7 x$. Find $\mathrm{goh}(\mathrm{x})$
Solution:

$\begin{aligned}
g(h(x)) & =2(3 x-5)^2-7(3 x-5) \\
& =2\left(9 x^2-30 x+25\right)-7(3 x-5) \\
& =18 x^2-60 x+50-21 x+35 \\
& =18 x^2-81 x+85
\end{aligned}$

Example 2: If $f: A \rightarrow B$ and $g: B \rightarrow C$ are both onto functions then $g \cdot f A \rightarrow C$ is

Solution:

Property of Composition of Functions -

If f: A → B and g: B → C are one-one, then g o f∶ A → C is also one-one
If f: A → B and g: B → C are onto, then g o f∶ A → C is also onto
If g o( f) is one-one, Then f is one-one.
If g o( f) is onto, Then g is onto.

It must be an onto function

Example 3: If $f(x)=x+3$ then which of the following $g(x)$ satisfies $g \circ f(x)=I_{\text {? }}$ ?
1) $g(x)=x+3$
2) $g(x)=x$
3) $g(x)=x-3$
4) $g(x)=x+2$

Solution:

$g(f(x))=g(x-3)=x+3-3=x$

Alternate Method

Clearly g(x) should be the inverse of f(x)

f(x) = y = x + 3

x = y - 3

So g(x) = x - 3

Hence, the answer is the option 3.

Example 4: If $f(x)=e^x$; then find $g(x)$ such that $g \circ f(x)=x$
1) $\ln x$
2) $\log _{10} x$
3) $e^x$
4) $x$

Solution:

$\text { If } g(x)=\ln x ; g(f(x))=g\left(e^x\right)=\ln \left(e^x\right)=x$

Hence, the answer is the option 1.
Example 5: If $f(x)=I_{A \text { and }} g(x)=e^x$, then $g \circ f(x)=$
Solution:

$g \circ f(x)=g(f(x))=g(x)=e^x$