Conjugate of a Matrix

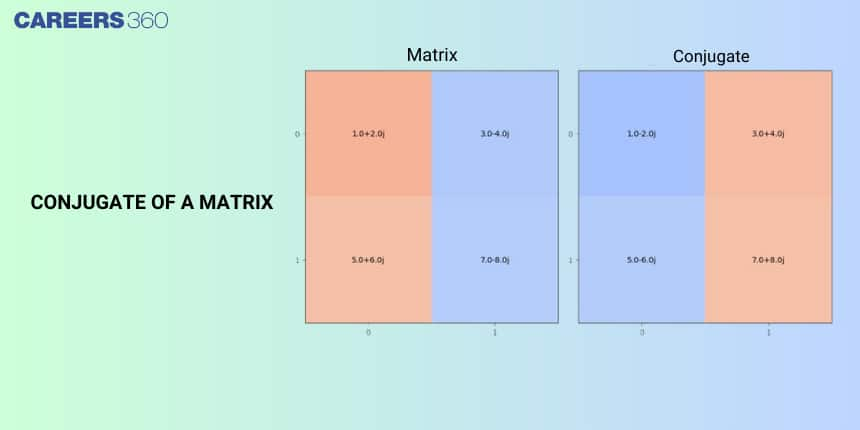
What is the Conjugate of a Matrix?

The conjugate of a matrix is formed by taking the complex conjugate of each element in the matrix. If a matrix contains complex numbers, the conjugate matrix helps simplify operations in linear algebra and complex arithmetic. This concept is essential when working with Hermitian, unitary, or other complex-valued matrices.

Conjugate Matrix Definition

If $A = [a_{ij}]$ is a matrix where each $a_{ij}$ can be a complex number, then the conjugate of matrix $A$, denoted by $\overline{A}$, is defined as:

$\overline{A} = [\overline{a_{ij}}]$

Example: If

$A = \begin{bmatrix} 3 + 2i & -i \\ 5 & 4 - i \end{bmatrix}$,

then

$\overline{A} = \begin{bmatrix} 3 - 2i & i \\ 5 & 4 + i \end{bmatrix}$

Difference Between Conjugate and Transpose

• Transpose of $A$, denoted $A^T$, flips rows and columns.

• Conjugate of $A$, denoted $\overline{A}$, changes the sign of imaginary parts.

• Conjugate Transpose, denoted $A^H$ or $A^H$, combines both:

$A^H = (\overline{A})^T$

So if

$A = \begin{bmatrix} 2 + i & 3 \\ 4i & 5 - i \end{bmatrix}$,

then

$A^H = \begin{bmatrix} 2 - i & -4i \\ 3 & 5 + i \end{bmatrix}$

Notation Used for Conjugate of Matrix

• Conjugate: $\overline{A}$ or sometimes $A^*$

• Transpose: $A^T$

• Conjugate Transpose: $A^H$ or $A^H$

In contexts involving complex conjugate of a matrix, it's important to distinguish between these symbols to avoid confusion.

The transpose conjugate of a matrix

The transpose of a conjugate matrix A is called the transposed conjugate of A and is denoted by A’. The conjugate of the transpose of A is the same as the transpose of the conjugate of A

$\begin{aligned} & \text { i.e. } \mathrm{A}^\theta=(\overline{\mathrm{A}})^{\prime}=\overline{\left(\mathrm{A}^{\prime}\right)} \\ & \mathrm{A}=\left[\begin{array}{ccc}1+2 i & 3 i & 5+4 i \\ 2 i-1 & 1-i & 0 \\ 3+i & 1+i & 12\end{array}\right] \\ & \overline{\mathrm{A}}=\left[\begin{array}{ccc}1-2 i & -3 i & 5-4 i \\ -2 i-1 & 1+i & 0 \\ 3-i & 1-i & 12\end{array}\right] \\ & (\overline{\mathrm{A}})^{\prime}=\left[\begin{array}{ccc}1-2 i & -2 i-1 & 3-i \\ -3 i & 1+i & 1-i \\ 5-4 i & 0 & 12\end{array}\right]\end{aligned}$

Properties of Conjugate Matrices

The conjugate of a matrix exhibits predictable behaviours under common matrix operations. These algebraic properties of conjugate matrices are essential when working with complex-valued linear systems, eigenvalues, or Hermitian matrices.

Basic Algebraic Properties

Let $A$ be a complex matrix. Then:

1. Double Conjugate:
   $\overline{(\overline{A})} = A$
   Taking the conjugate of a conjugate matrix gives the original matrix.

2. Conjugate of a Sum:
   $\overline{A + B} = \overline{A} + \overline{B}$
   The conjugate distributes over addition.

3. Conjugate of Scalar Multiple:
   If $k$ is a complex scalar, then
   $\overline{kA} = \overline{k} \cdot \overline{A}$

4. Conjugate of a Product:
   For two conformable matrices $A$ and $B$,
   $\overline{AB} = \overline{A} \cdot \overline{B}$

These rules help simplify expressions involving conjugate matrices during algebraic manipulation.

Interaction with Addition, Multiplication, and Scalar Operations

These properties make working with the complex conjugate of a matrix as intuitive as with real matrices:

• Addition:
  $\overline{A + B} = \overline{A} + \overline{B}$

• Multiplication:
  $\overline{AB} = \overline{A} \cdot \overline{B}$
  (only valid if $A$ and $B$ are conformable)

• Scalar Multiplication:
  $\overline{kA} = \overline{k} \cdot \overline{A}$
  where $k \in \mathbb{C}$.

These are used extensively in problems involving unitary matrices and complex matrix transformations.

Conjugate of a Matrix and Determinants

The determinant of a conjugate matrix has a simple relationship with the determinant of the original matrix:

$\det(\overline{A}) = \overline{\det(A)}$

This is particularly useful in proofs and simplifications involving complex-valued determinants and matrix inverses.

Applications of the Conjugate Matrix

Understanding the conjugate of a matrix is crucial in fields that involve complex numbers and matrix operations. The concept appears frequently in solving complex linear systems, constructing Hermitian and Unitary matrices, and modeling physical phenomena in quantum mechanics and signal processing.

Use in Solving Complex Linear Systems

In complex systems, the coefficient matrix often contains imaginary numbers. To simplify or solve such systems, we often use the conjugate matrix or the conjugate transpose (also called the Hermitian transpose).

For a complex system $A\vec{x} = \vec{b}$, pre-multiplying both sides by $\overline{A}^T$ gives:

$\overline{A}^T A \vec{x} = \overline{A}^T \vec{b}$

This transformation results in a real, symmetric matrix on the left-hand side (if $A$ is full rank), making it easier to solve.

Role in Hermitian and Unitary Matrices

• A matrix $A$ is Hermitian if:
  $A = \overline{A}^T$
  Hermitian matrices have real eigenvalues and play a major role in complex vector spaces.

• A matrix $U$ is Unitary if:
  $U \cdot \overline{U}^T = I$
  where $I$ is the identity matrix. Unitary matrices preserve vector norms and are the complex analog of orthogonal matrices.

In both cases, the complex conjugate of a matrix is essential for defining and verifying these properties.

Importance in Quantum Mechanics and Signal Processing

In quantum mechanics, state vectors and operators are represented using complex matrices. Observables are modelled by Hermitian matrices, which ensure real eigenvalues (measurable quantities).

In signal processing, especially in Fourier analysis and complex filtering, conjugation helps handle phase and frequency components. For example, the Fourier transform of a real-valued signal satisfies:

$\overline{X(f)} = X(-f)$

which is rooted in the concept of conjugates.

The conjugate matrix thus serves as a foundational tool in both theoretical and applied domains involving complex-valued data.

Solved Examples Based on Conjugate Matrix

Example 1: Find the conjugate of the matrix $\mathrm{A} = \left[\begin{array}{ccc} 2i & 3+4i & 7 \\ 3+4i & 9 & 4+5i \\ 7 & 4+5i & 3+7i \end{array}\right]$

Solution:

Given:

$A = \left[\begin{array}{ccc} 2i & 3+4i & 7 \\ 3+4i & 9 & 4+5i \\ 7 & 4+5i & 3+7i \end{array}\right]$

Taking the complex conjugate of each element:

$\bar{A} = \left[\begin{array}{ccc} -2i & 3-4i & 7 \\ 3-4i & 9 & 4-5i \\ 7 & 4-5i & 3-7i \end{array}\right]$

Hence, the required answer is:

$\left[\begin{array}{ccc} -2i & 3-4i & 7 \\ 3-4i & 9 & 4-5i \\ 7 & 4-5i & 3-7i \end{array}\right]$

Example 2: If matrix $B=\bar{A}, C=\bar{B}, D=\bar{C}$, so on then $\bar{G}=$
Solution:
Property of Conjugate: $\overline{(\bar{A})} = A$

Conjugate of a matrix $A$ is denoted by $\bar{A}$

$B = \bar{A}$

$C = \bar{B} = \overline{\bar{A}} = A$

Similarly, $G = A$

$\bar{G} = \bar{A} = B$

$\bar{G} = B$

Hence, the required answer is B.

Example 3: If $A_{2 \times 2}$ is a matrix such that $a_{i j}=(\omega)^{i+j}$ where $\omega$ is the cube root of unity then $B=A+\bar{A}$. Find $\bar{B}$.
Solution:
Conjugate of a Sum of Matrices

We verify the identity: $\overline{A + B} = \bar{A} + \bar{B}$

The conjugate of matrix $A$ is denoted by $\bar{A}$.

Let $A = \begin{bmatrix} \omega^{(1+1)} & \omega^{(1+2)} \\ \omega^{(2+1)} & \omega^{(2+2)} \end{bmatrix}$

So, $A = \begin{bmatrix} \omega^2 & \omega^3 \\ \omega^3 & \omega^4 \end{bmatrix}$

Since $\omega^3 = 1$ and $\omega^4 = \omega$, we simplify:

$A = \begin{bmatrix} \omega^2 & 1 \\ 1 & \omega \end{bmatrix}$

Now, conjugate of $A$:

$\bar{A} = \begin{bmatrix} \omega & 1 \\ 1 & \omega^2 \end{bmatrix}$

Add $A + \bar{A}$:

$A + \bar{A} = \begin{bmatrix} \omega^2 + \omega & 2 \\ 2 & \omega + \omega^2 \end{bmatrix}$

Now use identity: $\omega + \omega^2 = -1$, so:

$A + \bar{A} = \begin{bmatrix} -1 & 2 \\ 2 & -1 \end{bmatrix}$

Let $B = \begin{bmatrix} -1 & 2 \\ 2 & -1 \end{bmatrix}$

Clearly, $\bar{B} = \begin{bmatrix} -1 & 2 \\ 2 & -1 \end{bmatrix}$

Hence, the required answer is $\left[\begin{array}{cc}-1 & 2 \\ 2 & -1\end{array}\right]$

Example 4: What is the transpose conjugate of $\left[\begin{array}{cc}i+3 & i-3 \\ 0 & i+1\end{array}\right]$

Solution:

The transpose conjugate of a Matrix -

It is denoted by $\mathrm{A}^\theta$ and $\mathrm{A}^\theta=(\overline{\mathrm{A}})^{\prime}$

$A = \begin{bmatrix} i+3 & i-3 \\ 0 & i+1 \end{bmatrix}$

$\bar{A} = \begin{bmatrix} -i+3 & -i-3 \\ 0 & -i+1 \end{bmatrix}$

$(\bar{A})' = \begin{bmatrix} -i+3 & 0 \\ -i-3 & -i+1 \end{bmatrix}$

Hence, the required answer is $\left[\begin{array}{cc}-i+3 & 0 \\ -i-3 & -i+1\end{array}\right]$

Example 5: If $\mathrm{A}^*=\mathrm{B}$ and $\bar{B}=C$, then what will be relation between A and C ?

1) $\mathrm{A}=\mathrm{C}^{\prime}$

2) $A=\bar{C}$

3) $\mathrm{C}=\mathrm{A}^{\prime}$

4) $C=\bar{A}$

Solution:

Property of Transpose Conjugate -

$\left(A^{\theta}\right)^{\theta}=A$ wherein

$A^{\theta}$ is the conjugate matrix of $A$

Since $B=A^*=\overline{\left(A^{\prime}\right)}$

$\therefore C=\bar{B}=\left(\overline{\overline{A^{\prime}}}\right)=A^{\prime}$

Hence, the answer is option 3.

List of Topics Related to the Conjugate of a Matrix

Explore key matrix concepts that often connect with the conjugate of a matrix, including foundational types like triangular matrices, orthogonal matrices, and operations such as addition and multiplication. Also understand how conjugation relates to Hermitian, skew-Hermitian, and idempotent matrices, crucial in linear algebra and complex matrix analysis.

• Types of Matrices

• Triangular Matrix (Upper and Lower)

• Orthogonal Matrix

• Hermitian matrix & Skew Hermitian Matrix

• Idempotent Matrix

NCERT Resources

Access essential NCERT resources for Class 12 Maths Chapter 3 – Matrices, including concise revision notes, detailed solutions, and well-structured exemplar problems. These materials are designed to strengthen your understanding of matrices, covering concepts like matrix operations, conjugate matrix, and types of matrices in line with the CBSE syllabus.

Practice Questions based on the Conjugate of a Matrix

Sharpen your conceptual clarity with these MCQ-based practice questions on the conjugate of a matrix. These cover a wide range of topics such as matrix operations, Hermitian and skew-Hermitian matrices, symmetric matrices, and other types of matrices. These questions are ideal for self-assessment and revision for board exams, competitive tests, and strengthening your grasp on conjugate matrix concepts.

Conjugate of a Matrix MCQ - Practice Questions & Answers

You can practice the questions based on the next topics of matrices:

• Symmetric & Skew Symmetric Matrix - Practice Question MCQ

• Hermitian Matrix - Practice Question MCQ

• Skew Hermitian Matrix - Practice Question MCQ

• Trace Of A Matrix And Properties - Practice Question MCQ

• Orthogonal Matrix, Unitary Matrix, Idempotent Matrix - Practice Question MCQ

• Types of Matrices MCQ - Practice Questions MCQ