Coordinate Geometry
Imagine you are trying to locate a point on a map: how would you describe its exact position? This is exactly what coordinate geometry helps us do in mathematics. Coordinate geometry, also called analytical geometry, studies points, lines, and shapes using a pair of numbers called coordinates $(x, y)$ on a Cartesian plane. By linking algebra and geometry, it allows us to calculate distance, midpoints, slopes, and even find equations of lines and shapes easily. In this article, we will explore all the key concepts, formulas, and NCERT resources for coordinate geometry for Class 10, making it simple and practical for exams.
What Is Coordinate Geometry
Coordinate geometry, also called analytical geometry, is the branch of mathematics that studies the position of points, lines, and curves on a plane using coordinates $(x, y)$. It connects algebra and geometry, making it easier to calculate distance between points, midpoints, slopes of lines, and equations of straight lines and circles in mathematics. Coordinate geometry is widely used in physics to represent motion and forces, in engineering and construction for designing structures, and in astronomy to determine distances and positions of celestial objects. It also helps in graphical representation of functions and shapes, giving a clear visual understanding of mathematical concepts.
Coordinate Geometry - Basic Terminologies and Definitions
Straight Lines: In coordinate geometry, a straight line is represented by an equation in the form $y = mx + c$, where $m$ is the slope and $c$ is the y-intercept. For example, the line $y = 2x + 3$ cuts the y-axis at $3$ and rises 2 units for every 1 unit it moves along the x-axis.
Inclination of a Line: In a coordinate plane, a line forms an angle with the positive direction of the x-axis. This angle, measured anticlockwise, is called the inclination of the line. For example, if a line rises 3 units vertically for 4 units horizontally, its inclination $\theta$ can be found using $ \tan \theta = \frac{3}{4} $.
It forms the basis and foundation of advanced topics such as conic sections including hyperbola, parabola, circle and ellipse, that play a major role in higher level mathematics.
Circle: A circle is the set of all points in a coordinate plane that are equidistant from a fixed point called the center. Example: The circle with center at $(0,0)$ and radius $5$ has the equation $x^2 + y^2 = 25$.
Basics of the Cartesian Plane
The Cartesian plane is the foundation of coordinate geometry, allowing us to locate points, lines, and shapes using algebra and geometry together. It helps students visualize and analyze geometric problems easily.
X-axis, Y-axis, and Origin
The Cartesian plane has two perpendicular number lines: the x-axis (horizontal) and the y-axis (vertical). The intersection point is the origin $(0,0)$, and every point is written as $(x, y)$.
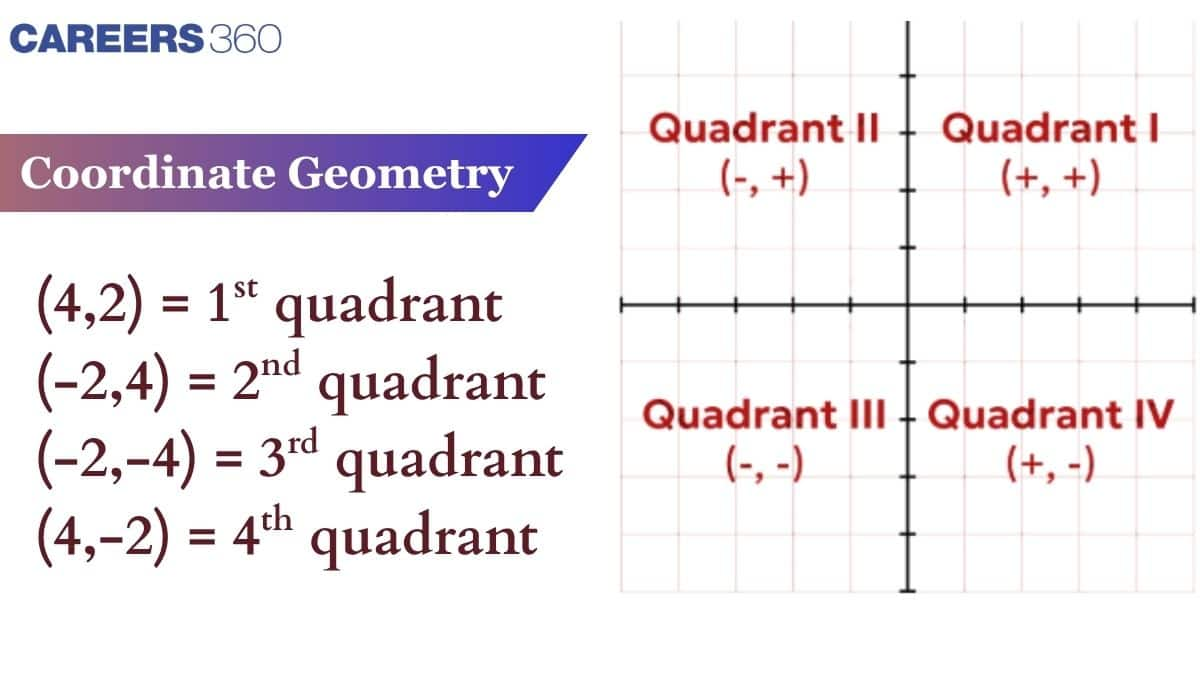
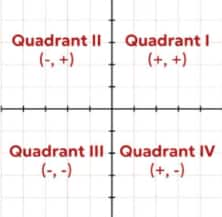
Quadrants and Coordinates of a Point
The plane is divided into four quadrants:
Quadrant I: $x > 0, y > 0$
Quadrant II: $x < 0, y > 0$
Quadrant III: $x < 0, y < 0$
Quadrant IV: $x > 0, y < 0$
Example: The point $(-3, 4)$ lies in Quadrant II.
Plotting Points on the Cartesian Plane
To plot a point $(x, y)$, start at the origin, move $x$ units along the x-axis, then $y$ units along the y-axis. This method helps in graphical visualization of points and lines.
Distance and Midpoint Formulas
Distance and midpoint formulas are essential to calculate lengths of segments and middle points, widely used in geometry, physics, and engineering.
Distance Between Two Points $(x_1, y_1)$ and $(x_2, y_2)$
The distance formula calculates the length of a line segment:
$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $
Example: Distance between $(1, 2)$ and $(4, 6)$ is $5$.
Midpoint of a Line Segment
The midpoint formula finds the point exactly in the middle of a segment:
$ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) $
Example: Midpoint of $(2, 3)$ and $(6, 7)$ is $(4, 5)$.
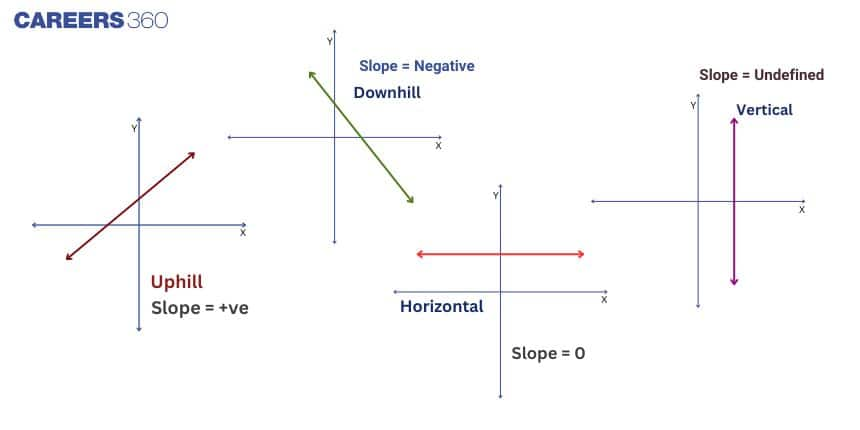
Slope of a Line and Angle with X-Axis
Slope tells us how steep a line is, and the angle of inclination helps in understanding the line’s direction on the plane.
Formula for Slope $(m = \frac{y_2 - y_1}{x_2 - x_1})$
Slope measures how steep a line is. Positive slope rises, negative slope falls.
Positive, Negative, Zero, and Undefined Slopes
Positive slope: Line rises from left to right
Negative slope: Line falls from left to right
Zero slope: Horizontal line
Undefined slope: Vertical line
Angle of Inclination of a Line
The angle $\theta$ a line makes with the positive x-axis is:
$ m = \tan \theta $
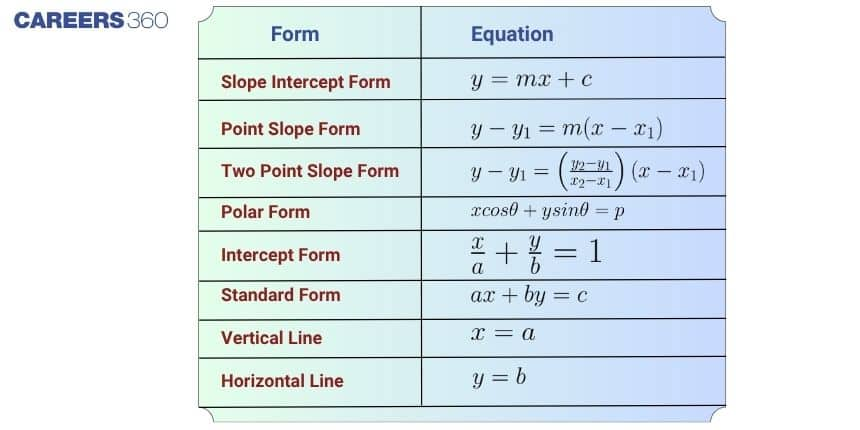
Equations of a Line
Equations of a line allow us to represent lines algebraically, making it easier to solve geometric problems and calculate intersections.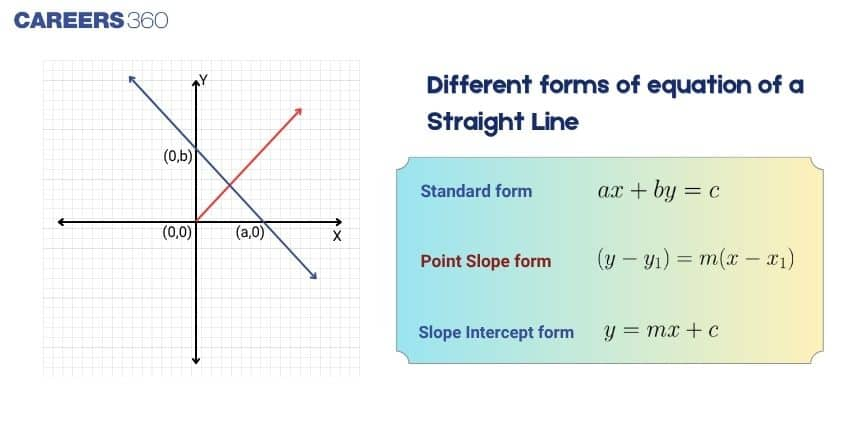
Slope-Intercept Form $(y = mx + c)$
Represents a line with slope $m$ and y-intercept $c$.
Point-Slope Form $(y - y_1 = m(x - x_1))$
Used when a line passes through a point $(x_1, y_1)$ with slope $m$.
General Form $(Ax + By + C = 0)$
A standard form for any straight line.
Horizontal and Vertical Lines
Horizontal line: $y = k$
Vertical line: $x = h$
Section Formula and Coordinate Geometry Applications
The section formula helps divide a line segment internally or externally and is widely used in physics, engineering, and real-life mapping problems.
Internal Division of a Line Segment
A point dividing a segment internally in the ratio $m:n$:
$ P = \left( \frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n} \right) $
External Division of a Line Segment
A point dividing a segment externally in the ratio $m:n$:
$ P = \left( \frac{mx_2 - nx_1}{m-n}, \frac{my_2 - ny_1}{m-n} \right) $
Important Formulas in Coordinate Geometry
Equation of a Line: The general equation of a line is $ax + by + c = 0$.
Distance Formula: The distance $D$ between two points $(x_1, y_1)$ and $(x_2, y_2)$ is
$D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Slope of a Line: For the line $ax + by + c = 0$, the slope $m$ is
$m = -\frac{a}{b}$.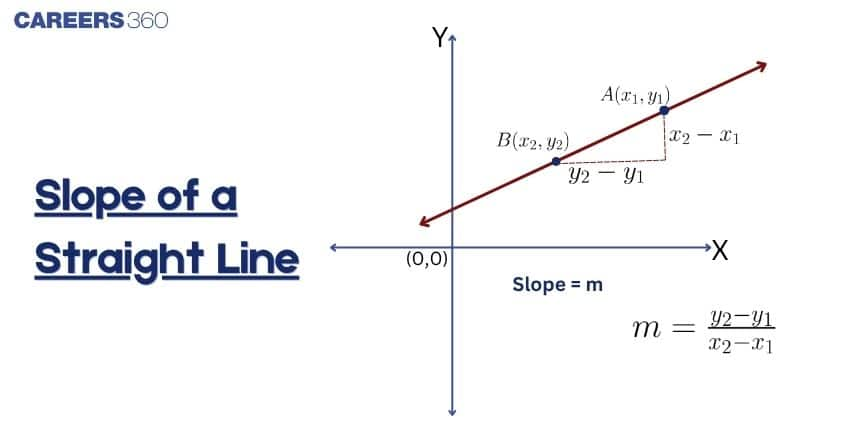
Slope of parallel and perpendicular lines: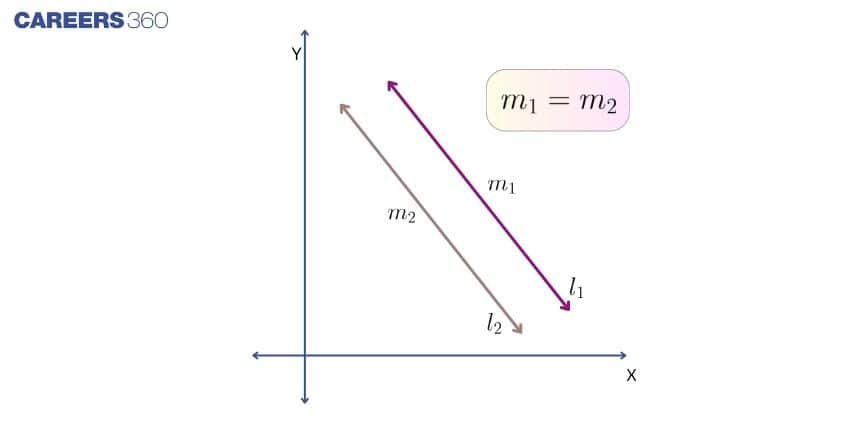
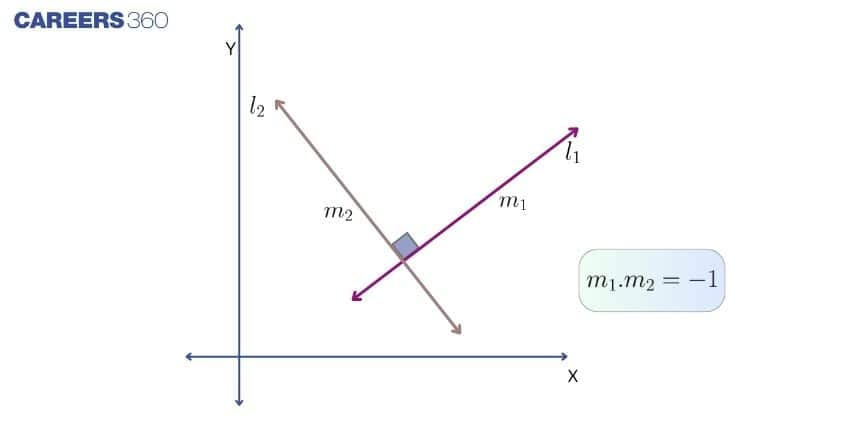
Angle Between Two Lines: If two lines have slopes $m_1$ and $m_2$, the angle $\theta$ between them is
$\theta = \tan^{-1} \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right|$.
Distance of a Point from a Line: The distance $d$ of a point $(x_1, y_1)$ from the line $ax + by + c = 0$ is
$d = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}$.
Distance Between Two Parallel Lines: For two parallel lines of slope $m$, $y = mx + c_1$ and $y = mx + c_2$, the distance $d$ between them is
$d = \frac{|c_1 - c_2|}{\sqrt{1 + m^2}}$.
Recommended Books for Coordinate Geometry
Find the best books for Class 10 coordinate geometry that simplify concepts, provide solved examples, and enhance problem-solving skills for board and competitive exams.
| Book Title | Author/Publisher |
|---|---|
| Mathematics for Class 10 | R.D. Sharma |
| NCERT Mathematics Textbook | NCERT |
| Mathematics Success Guide | R.S. Aggarwal |
| Quick Mathematics | M.L. Aggarwal |
| Coordinate Geometry Made Easy | S. K. Goyal |
NCERT Resources
Access NCERT textbooks, solutions, and practice exercises for coordinate geometry to build strong fundamentals and excel in Class 10 mathematics exams.
NCERT Maths Class 10 Notes for Chapter 7 - Coordinate Geometry
NCERT Maths Class 10 Solutions for Chapter 7 - Coordinate Geometry
NCERT Maths Class 10 Exemplar Solutions for Chapter 7 - Coordinate Geometry
Frequently Asked Questions (FAQs)
Coordinate geometry is a branch of mathematics where points, lines, and curves are represented on a plane using algebraic equations. It combines geometry and algebra for easy problem-solving.
Use the distance formula: $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Slope measures the steepness of a line: $m = \frac{y_2 - y_1}{x_2 - x_1}$. Positive slope rises, negative slope falls.
For internal division: $P = \left( \frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n} \right)$; for external division: $P = \left( \frac{mx_2 - nx_1}{m-n}, \frac{my_2 - ny_1}{m-n} \right)$.
Use $(x - h)^2 + (y - k)^2 = r^2$, where $(h, k)$ is the center and $r$ is the radius.