Cross Product - Definition, Formula, Rules and Examples

Multiplication (or product) of two vectors is defined in two ways, namely, dot (or scalar) product where the result is a scalar, and vector (or cross) product where the result is a vector. Based on these two types of products for vectors, we have various applications in geometry, mechanics, and engineering. In real life, we use vector products when installing a solar panel on a roof.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is Vector( or cross-product)?
2. Right Hand Rule - Cross Product of Two Vectors
3. Properties of Vector Product
4. Cross Product of Perpendicular Vectors
5. Cross Product of Parallel vectors
6. Triple Cross Product
7. Solved Examples Based on Cross-product
8. Summary

In this article, we will cover the concept of cross-product. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of fourty five questions have been asked on this topic in JEE Main from 2013 to 2023 including two in 2020, eleven in 2021, fourteen in 2022, and seventeen in 2023.

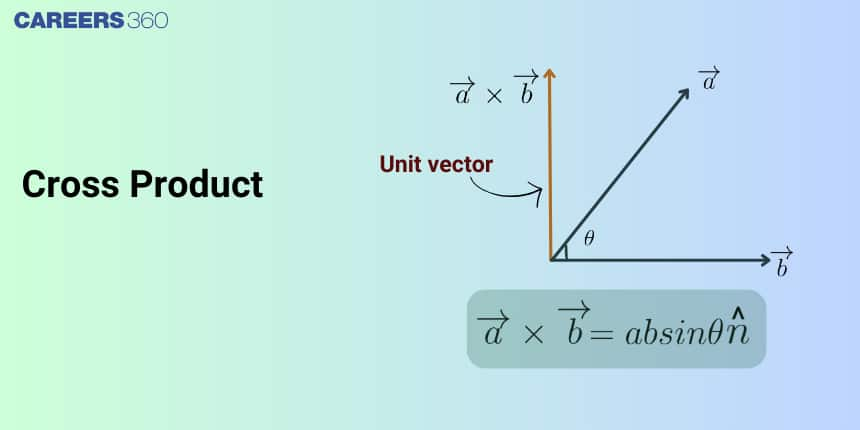
What is Vector( or cross-product)?

The cross-product is a binary operation on two vectors in three-dimensional space. It results in a vector that is perpendicular to both vectors. The vector product of two vectors$\mathbf{a}$ and $\mathbf{b}$, is denoted by $\mathbf{a}\times \mathbf{b}$. Its resultant vector is perpendicular to $\mathbf{a}$ and $\mathbf{b}$.

Cross Product Formula
The vector product of two nonzero vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, is denoted by $\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}$ and defined as,

$\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}=|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|\sin \theta \hat{\mathbf{n}}$

where $\theta$ is the angle between $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}},0\le \theta \le \pi$ and $\hat{\mathrm{n}}$ is a unit vector perpendicular to both $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, such that $\overrightarrow{\mathbf{a}},\overrightarrow{\mathbf{b}}$ and $\hat{\mathrm{n}}$ form a right-hand system.

Right Hand Rule - Cross Product of Two Vectors

In the right-hand rule, we can stretch our right hand so that the index finger of the right hand is in the direction of the first vector and the middle finger is in the direction of the second vector. Then, the thumb of the right hand indicates the direction or unit vector n. With the help of the right-hand rule, we can easily show that vectors’ cross product is not commutative. If we have two vectors A and B, then the diagram for the right-hand rule is as follows:

Observe that, the direction of $\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}$ is opposite to that of $\overrightarrow{\mathbf{b}}\times \overrightarrow{\mathbf{a}}$ as shown in the figure.
i.e. $\overrightarrow{a}\times \overrightarrow{b}=-\overrightarrow{a}\times \overrightarrow{b}$

So the vector product is not commutative.

The cross-product is just a shorthand invented for the purpose of quickly writing down the angular momentum of an object. Here's how the cross-product arises naturally from angular momentum. Recall that if we have a fixed axis and an object at distance r away with velocity v and mass m is moving around the axis in a circle, then the magnitude of the angular momentum is m*|r|*|v| where |r| is the magnitude of vector r. But what direction should the angular momentum vector point in? Well, if you follow the path of the object, it lies in a plane, an infinite two-dimensional surface. One way to represent a plane is to write down two different vectors that lie in the plane.

Properties of Vector Product

1. $\overrightarrow{a}\times \overrightarrow{b}$ is a vector.
2. Let $\overrightarrow{a}$ and $\overrightarrow{b}$ be two nonzero vectors. Then $\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{0}$ if and only if $\overrightarrow{a}$ and $\overrightarrow{b}$ are parallel (or collinear) to each other, i.e.,

$\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{0}\iff \overrightarrow{a}\Vert \overrightarrow{b}$
In particular, $\overrightarrow{a}\times \overrightarrow{a}=\overrightarrow{0}$ and $\overrightarrow{a}\times (-\overrightarrow{a})=\overrightarrow{0}$, since in the first situation, $\theta =0$ and in the second one, $\theta =\pi$.
3. If $\theta =\frac{\pi }{2}$, then $\overrightarrow{a}\times \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|$.

$\begin{array}{rl}& \text{ 4. From the property 2. and }3\\ & \hat{i}\times \hat{i}=\hat{j}\times \hat{j}=\hat{k}\times \hat{k}=\overrightarrow{0}\\ & \hat{i}\times \hat{j}=\hat{k},\hat{j}\times \hat{k}=\hat{i},\hat{k}\times \hat{i}=\hat{j}\\ & \text{ and also, }\\ & \hat{j}\times \hat{i}=-\hat{k},\hat{k}\times \hat{j}=-\hat{i}\text{ and }\hat{i}\times \hat{k}=-\hat{i}\end{array}$

5. Vector product is not associative, i.e. $\overrightarrow{a}\times \overrightarrow{b}\ne \overrightarrow{b}\times \overrightarrow{a}$
6. If $\overrightarrow{a}$ and $\overrightarrow{b}$ are two vectors and $m$ is a scalar, then $m\overrightarrow{a}\times \overrightarrow{b}=m(\overrightarrow{a}\times \overrightarrow{b})=\overrightarrow{a}\times m\overrightarrow{b}$
7. If $\overrightarrow{a}$ and $\overrightarrow{b}$ are two vectors and $m,n$ are scalars, then $m\overrightarrow{a}\times n\overrightarrow{b}=mn(\overrightarrow{a}\times \overrightarrow{b})=m(n\overrightarrow{a}\times \overrightarrow{b})=n(m\overrightarrow{a}\times \overrightarrow{b})$
8. For any three vectors $\overrightarrow{a},\overrightarrow{b}$ and $\overrightarrow{c}$, we have
(i) $\overrightarrow{a}\times (\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}$
(ii) $\overrightarrow{a}\times (\overrightarrow{b}-\overrightarrow{c})=\overrightarrow{a}\times \overrightarrow{b}-\overrightarrow{a}\times \overrightarrow{c}$

Proof:

$\begin{array}{rl}\overrightarrow{a}\times \overrightarrow{b}=& (a_1\hat{i}+a_2\hat{j}+a_3\hat{k})\times (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})\\ =& a_1{b}_1(\hat{i}\times \hat{i})+a_1{b}_2(\hat{i}\times \hat{j})+a_1{b}_3(\hat{i}\times \hat{k})+a_2{b}_1(\hat{j}\times \hat{i})\\ & +a_2{b}_2(\hat{j}\times \hat{j})+a_2{b}_3(\hat{j}\times \hat{k})+a_3{b}_1(\hat{k}\times \hat{i})+a_3{b}_2(\hat{k}\times \hat{j})+a_3{b}_3(\hat{k}\times \hat{k})\\ =& a_1{b}_2(\hat{i}\times \hat{j})-a_1{b}_3(\hat{k}\times \hat{i})-a_2{b}_1(\hat{i}\times \hat{j})\\ & ++a_2{b}_3(\hat{j}\times \hat{k})+a_3{b}_1(\hat{k}\times \hat{i})-a_3{b}_2(\hat{j}\times \hat{k})\end{array}$
The angle between Two Vectors
If $\theta$ is the angle between the vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, then

$\sin \theta =\frac{|\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}|}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}$

Vector perpendicular to the plane of two given vectors

The unit vector perpendicular to the planeof $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ is $\frac{(\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}})}{|\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}|}$

Also, note that $-\frac{(\overrightarrow{a}\times \overrightarrow{b})}{|\overrightarrow{a}\times \overrightarrow{b}|}$is also a unit vector perpendicular to the plane of $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$.

Vectors of magnitude ‘λ’ perpendicular to the planeof $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ are given by $\pm \frac{\lambda (\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}})}{|\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}|}$

Cross Product of Perpendicular Vectors

The cross product of two vectors is equal to the product of their magnitude, which represents the area of a rectangle with sides X and Y.

If two vectors are perpendicular to each other, then the cross-product formula becomes:θ = 90 degrees.

We know that, sin 90° = 1.

$|\overrightarrow{a}\times \overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|$|

Cross Product of Parallel vectors

The cross product of two vectors is zero vectors if both vectors are parallel or opposite to each other. Conversely, if two vectors are parallel or opposite to each other, then their product is a zero vector. Two vectors have the same sense of direction.

We know that, $\sin 0^{\circ }=0$

$|\overrightarrow{a}\times \overrightarrow{b}|=0$ which is a unit vector

Triple Cross Product

The cross product of a vector with the cross product of the other two vectors is the triple cross product of the vectors. The resultant of the triple cross product is a vector. The resultant of the triple cross vector lies in the plane of the given three vectors. It is expressed as $\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})$

For three vectors $\overrightarrow{\mathbf{a}},\overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ vector triple product is defined as $\overrightarrow{\mathbf{a}}\times (\overrightarrow{\mathbf{b}}\times \overrightarrow{\mathbf{c}})$ $\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})=(\overrightarrow{a}\cdot \overrightarrow{c})\cdot \overrightarrow{b}-(\overrightarrow{a}\cdot \overrightarrow{b})\cdot \overrightarrow{c}$

Recommended Video Based on Cross-product

Solved Examples Based on Cross-product

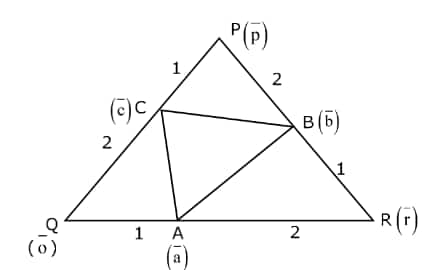
Example 1: Let PQR be a triangle. The points A, B, and C are on the sides QR, RP, and PQ respectively such that $\frac{QA}{AR}=\frac{RB}{BP}=\frac{PC}{CQ}=\frac{1}{2}$. Then $\frac{\text{ Area }(\mathrm{△}PQR)}{\text{ Area }(\mathrm{△}ABC)}$ is equal to

Solution

$\begin{array}{rl}& \bar{\mathrm{a}}=\frac{\bar{\mathrm{r}}}{3}\\ & \bar{\mathrm{b}}=\frac{\bar{\mathrm{b}}+2\bar{\mathrm{r}}}{3}\\ & \bar{\mathrm{c}}=\frac{2\bar{\mathrm{p}}}{3}\end{array}$

$\begin{array}{rl}& \mathrm{\Delta }\mathrm{PQR}=\frac{1}{2}|\bar{\mathrm{r}}\times \bar{\mathrm{p}}|\\ & \mathrm{\Delta }\mathrm{PQR}=\frac{1}{2}|\bar{\mathrm{a}}\times \bar{\mathrm{b}}+\bar{\mathrm{b}}\times \bar{\mathrm{c}}+\bar{\mathrm{c}}\times \bar{\mathrm{a}}\\ & =\frac{1}{2}|\frac{\bar{\mathrm{r}}\times \bar{\mathrm{p}}}{9}+\frac{4(\bar{\mathrm{r}}\times \bar{\mathrm{p}})}{9}+\frac{2}{9}\bar{\mathrm{p}}\times \bar{\mathrm{r}}|\\ & =\frac{1}{18}|3(\bar{\mathrm{r}}\times \bar{\mathrm{p}})|\\ & \text{ Hence }\frac{|\mathrm{\Delta }\mathrm{PQR}|}{|\mathrm{\Delta }\mathrm{ABC}|}=3\end{array}$

Example 2: Let $\overrightarrow{\mathrm{a}}=2\hat{\mathrm{i}}-7\hat{\mathrm{j}}+5\mathrm{k},\overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}+\mathrm{k}$ and $\overrightarrow{\mathrm{c}}=\hat{\mathrm{i}}+2\hat{\mathrm{j}}-3\mathrm{k}$ be three given vectors. If $\overrightarrow{r}$ is a vector such that $\overrightarrow{\mathrm{r}}\times \overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{c}}\times \overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{r}}\cdot \overrightarrow{\mathrm{b}}=0$, then $|\overrightarrow{\mathrm{r}}|$ is equal :
Solution

$\begin{array}{rl}& \overrightarrow{r}\times \overrightarrow{a}=\overrightarrow{c}\times \overrightarrow{a}\\ & \Rightarrow (\overrightarrow{r}-\overrightarrow{c})\times \overrightarrow{a}=0\Rightarrow \overrightarrow{r}-\overrightarrow{c}=\lambda \overrightarrow{a}(\overrightarrow{r}-\overrightarrow{c}\mathrm{\&}\text{ a b are parallel })\\ & \Rightarrow \overrightarrow{r}=\overrightarrow{c}+\lambda \overrightarrow{a}\\ & \Rightarrow \overrightarrow{r}\cdot \overrightarrow{b}=\overrightarrow{c}\cdot \overrightarrow{b}+\lambda \overrightarrow{a}\cdot \overrightarrow{b}\\ & 0=(1-3)+\lambda (2+5)\Rightarrow \lambda =\frac{2}{7}\end{array}$
Hence, $\overrightarrow{r}=\overrightarrow{c}+\frac{2\overrightarrow{a}}{7}$

$\begin{array}{rl}& \overrightarrow{r}\Rightarrow \frac{11}{7}\hat{ı}-\frac{11}{7}\hat{k}\\ & |\overrightarrow{r}|=\sqrt{{\left(\frac{11}{7}\right)}^2+{(-\frac{11}{7})}^2}\Rightarrow r=\frac{11\sqrt{2}}{7}\end{array}$
Hence, the answer is $\frac{11}{7}\sqrt{2}$

Example 3: Let $\tilde{\mathrm{a}}=3\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$ and $\tilde{\mathrm{c}}=2\hat{\mathrm{i}}-3\hat{\mathrm{j}}+3\hat{\mathrm{k}}$. If $\tilde{\mathrm{b}}$ is a vector such that $\tilde{\mathrm{a}}=\tilde{\mathrm{b}}\times \tilde{\mathrm{c}}$ and $|\tilde{\mathrm{b}}{|}^2=50$ then $|72-|\tilde{\mathrm{b}}+{\tilde{\mathrm{c}}|}^2\mid$ is equal to $$ .

Solution: $|\overrightarrow{a}|=\sqrt{11},|\overrightarrow{c}|=\sqrt{22}$

$\begin{array}{rl}& |\overrightarrow{a}|=|\overrightarrow{b}\times \overrightarrow{c}|=|\overrightarrow{b}||\overrightarrow{c}|\sin \theta \\ & \sqrt{11}=\sqrt{50}\sqrt{22}\sin \theta \\ & \Rightarrow \sin \theta =\frac{1}{10}\end{array}$
$\begin{array}{rl}& |\overrightarrow{b}+\overrightarrow{c}{|}^2=|\overrightarrow{b}{|}^2+|\overrightarrow{c}{|}^2+2\overrightarrow{b}\cdot \overrightarrow{c}\\ & =|\overrightarrow{b}{|}^2+|\overrightarrow{c}{|}^2+2|\overrightarrow{b}|\overrightarrow{c}\mid \cos \theta \\ & =50+22+2\times \sqrt{50}\times \sqrt{22}\times \frac{\sqrt{99}}{10}\\ & =72+66\end{array}$

$72-|\overrightarrow{b}+\overrightarrow{c}{|}^2\mid =66$

Hence, the answer is 66.

Example 4: Let $\overrightarrow{a}$ and $\overrightarrow{b}$ be two vectors such that $|\overrightarrow{a}|=\sqrt{14},|\overrightarrow{b}|=\sqrt{6}$ and $|\overrightarrow{a}\times \overrightarrow{b}|=\sqrt{48}$ Then $(\overrightarrow{a}\cdot \overrightarrow{b}{)}^2$ is equal to

Solution

$\begin{array}{rl}& |\overrightarrow{a}\times \overrightarrow{b}{|}^2=|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2-(\overrightarrow{a}\cdot \overrightarrow{b}{)}^2\\ & 48=14\times 6-(\overrightarrow{a}\cdot \overrightarrow{b}{)}^2\\ & (\overrightarrow{a}\cdot \overrightarrow{b}{)}^2=84-48\\ & (\overrightarrow{a}\cdot \overrightarrow{b}{)}^2=36\end{array}$

Hence, the answer is 36

Example 5: Let $\overrightarrow{\mathrm{a}}=\alpha \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{b}}=2\hat{\mathrm{i}}+\hat{\mathrm{j}}-\alpha \hat{\mathrm{k}},\alpha >0$. If the projection of $\overrightarrow{a}\times \overrightarrow{\mathrm{b}}$ on the vector $-\hat{\mathrm{i}}+2\hat{\mathrm{j}}-2\hat{\mathrm{k}}$ is 30 , then $\alpha$ is equal to:
Solution: $\Rightarrow \overrightarrow{a}\times \overrightarrow{b}=(1-\alpha )\hat{i}+({\alpha }^2-2)\hat{j}+(\alpha -2)\hat{k}$
Projection of $\overrightarrow{a}\times \overrightarrow{b}$ on $-\hat{i}+2\hat{ȷ}-2\hat{k}$

$\begin{array}{rl}& =\frac{(\overrightarrow{a}\times \overrightarrow{b})\cdot (-\hat{\mathrm{i}}+2\hat{\mathrm{j}}-2\hat{\mathrm{k}})}{3}\\ & =30\\ & \Rightarrow 2{\alpha }^2-\alpha -91=0\\ & \Rightarrow \alpha =7,-\frac{13}{2}\end{array}$

Hence, the answer is 7

Summary

The vector product, or cross product quantifies the relationship between vectors through both geometric insight and numerical calculation. Its properties of commutativity, distributivity, and facilitation of projection make it indispensable in fields ranging from physics and engineering to computer graphics. Knowledge of the scalar product helps in solving problems and advancing knowledge.