De-Morgan's Laws

De Morgan's Law in sets is one of the main concepts in the topic of sets, as it defines the properties of some operations on sets. De Morgan's Laws gives the relationship between union, complements and intersection of sets. De Morgan's Laws provide a way to simplify complex logical and set expressions by transforming them into an equivalent form. These laws are particularly useful in various fields such as computer science, digital logic design, and mathematics for simplifying expressions and proving equivalences. Now let us look in detail about what is the De Morgan's law.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. De Morgan's law in Sets
2. De Morgan's Law Formula
3. First Law:
4. De Morgan's Law Example
5. De Morgan's Law in Boolean Algebra
6. Solved Examples Based On the De-Morgan's Law

In this article, we will cover the concept of the De-Morgan's Law. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept, including one in 2022.

De Morgan's law in Sets

In set theory, the relationship between union, complements, and intersection is provided by De Morgan's law. It provides the relationship between AND, OR, and the variable's complements in Boolean algebra; in logic, it provides the relationship between AND, OR, or the statement's negation. De Morgan's Law allows us to optimize different boolean circuits that use logic gates to do the same task with a minimum amount of equipment.

According to De Morgan's Laws:

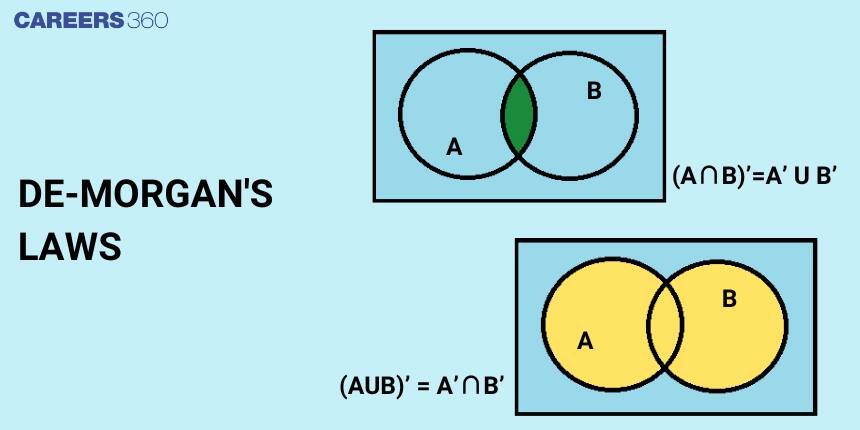
• The complement of the union of two sets is equal to the intersection of their individual complements.
• Additionally, the complement of the intersection of two sets is equal to the union of their individual complements.

De Morgan's Law Formula

De Morgan's Law Formula gives its first and second law and its truth tables.

First Law:

.The complement of the union of two sets is equal to the intersection of the complements of each set, according to the first application of De Morgan's law. If $A$ and $B$ are two sets, then First De Morgan's Law can be expressed mathematically as follows:

$
(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}
$

Where
$\cup$ stands for the Union operation between sets,' for the complement operation on a set, and $\cap$ for the intersection operation between sets.
Another name for it is De Morgan's Law of Union.

Second Law:

"The complement of intersection of two sets is equal to the union of the complements of each set," according to the second De Morgan's law. If $A$ and $B$ are two sets, then First De Morgan's Law can be expressed mathematically as follows:

$
(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}
$

Where
$\cup$ stands for the Union operation between sets,' for the complement operation on a set, and $\cap$ for the intersection operation between sets.
Another name for it is the Law of Intersection by De Morgan.

De Morgan's Law Proof

De Morgan's Law of Union: The complement of the union of the two sets $A$ and $B$ will be equal to the intersection of $A^{\prime}$ (complement of $A$) and $B ^{\prime}$(complement of $B$). This is also known as De Morgan's Law of Union. It can be represented as $(A ∪ B)^{\prime} = A^{\prime} ∩ B ^{\prime}$. We can also generalize this law.

Suppose we have $n$ sets given by $\{A1,A2,...,AnA1,A2,...,An\}$ then formula is given by $(⋃ni=1Ai)^{\prime}=⋂ni=1A^{\prime}i(⋃i=1nAi)^{\prime}=⋂i=1nAi^{\prime} $.

In set theory, Demorgan's law proves that the intersection and union of sets get interchanged under complementation. We can prove De Morgan's law both mathematically and by using truth tables.

1. $(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$

Let $x$ be any element in $(A \cup B)^{\prime}$

$
x \in(A \cup B)^{\prime} \Leftrightarrow x \notin(A \cup B)
$

$\Leftrightarrow x \notin A$ and $x \notin B$ (As $x$ does not belong to $A \cup B$, it cannot belong to both A and B )

$
\begin{aligned}
& \Leftrightarrow x \in A^{\prime} \text { and } x \in B^{\prime} \\
& \Leftrightarrow x \in\left(A^{\prime} \cap B^{\prime}\right) \\
\therefore x \in(A \cup B)^{\prime} \Leftrightarrow & x \in\left(A^{\prime} \cap B^{\prime}\right)
\end{aligned}
$

So, any element that belongs to $(A \cup B)^{\prime}$ also belongs to $\left(A^{\prime} \cap B^{\prime}\right)$, and vice versa

So, these sets have exactly the same elements, hence they are equal

De Morgan's Law of Intersection: The complement of the intersection of $A$ and $B$ will be equal to the union of $A^{\prime}$ and $B^{\prime}$. This condition is called De Morgan's law of Intersection. It can be given by $(A ∩ B)^{\prime} = A^{\prime} ∪ B^{\prime}$. Similarly, as above this law can be generalized by the formula $(⋂ni=1Ai)^{\prime}=⋃ni=1A^{\prime}i(⋂i=1nAi)^{\prime}=⋃i=1nAi^{\prime}$.

2. $(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}$

Let x be any element in $(A \cap B)^{\prime}$

$
x \in(A \cap B)^{\prime} \Leftrightarrow x \notin(A \cap B)
$

$\Leftrightarrow x \notin A$ or $x \notin B \quad$ (as $x \notin(A \cap B)$, means it is not common in $A$ and $B$, and thus either it is not in $A$ or not in $B$ )

$
\begin{aligned}
& \Leftrightarrow x \in A^{\prime} \text { or } x \in B^{\prime} \\
& \Leftrightarrow x \in\left(A^{\prime} \cup B^{\prime}\right) \\
& \therefore x \in(A \cap B)^{\prime} \Leftrightarrow x \in\left(A^{\prime} \cup B^{\prime}\right)
\end{aligned}
$

So, any element that belongs to $(A \cap B)^{\prime}$ also belongs to $\left(A^{\prime} \cup B^{\prime}\right)$, and vice versa

So, these sets have exactly the same elements, hence they are equal.

De Morgan's Law Truth Table

De Morgan's First Law:

$
\begin{array}{|l|l|l|l|l|l|l|}
\hline A & B & A \cup B & (A \cup B)^{\prime} & A^{\prime} & B^{\prime} & A^{\prime} \cap B^{\prime} \\
\hline 1 & 1 & 1 & 0 & 0 & 0 & 0 \\
\hline 1 & 0 & 1 & 0 & 0 & 1 & 0 \\
\hline 0 & 1 & 1 & 0 & 1 & 0 & 0 \\
\hline 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\hline
\end{array}
$

De Morgan's Second Law:

$
\begin{array}{|l|l|l|l|l|l|l|}
\hline A & B & A \cap B & (A \cap B)^{\prime} & A^{\prime} & B^{\prime} & A^{\prime} \cup B^{\prime} \\
\hline 1 & 1 & 1 & 0 & 0 & 0 & 0 \\
\hline 1 & 0 & 0 & 1 & 0 & 1 & 1 \\
\hline 0 & 1 & 0 & 1 & 1 & 0 & 1 \\
\hline 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\hline
\end{array}
$

De Morgan's Law Example

Let us understand De Morgan's law with the help of a simple example. Let the universal set $U=\{7,8,9,10,11,12,13\}$. The two subsets are given by $A=\{11$, $12,13\}$ and $B=\{7,8\}$.

• De Morgan's Law of Union Example: $(\mathrm{A} \cup \mathrm{B})=\{7,8,11,12,13\},(\mathrm{A} \cup$ $B)^{\prime}=\{9,10\} . A^{\prime}=\{7,8,9,10\}$ and $B^{\prime}=\{9,10,11,12,13\} . A^{\prime} \cap B^{\prime}=$ $\{9,10\}$. Thus, $(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
• De Morgan's Law of Intersection Example: $(A \cap B)=\varnothing,(A \cap B)^{\prime}=\{7$, $8,9,10,11,12,13\} . A^{\prime} \cup B^{\prime}=\{7,8,9,10,11,12,13\}$. Hence, (A $\cap$ $B)^{\prime}=A^{\prime} \cup B^{\prime}$

De Morgan's Law in Boolean Algebra

The De Morgan's Law in Boolean Algebra is

1. $\overline{A+B}=\bar{A} \cdot \bar{B}$
2. $\overline{A \cdot B}=\bar{A}+\bar{B}$

Now let;'s look into De Morgan's law in Boolean Algebra proof.

De Morgan's law in Boolean Algebra Proof

De Morgan's law in Boolean Algebra Proof is,

1. $\overline{A+B}=\bar{A} \cdot \bar{B}$
$\overline{A+B}=1-(A+B)$ (Complement property)
$\quad \quad \quad =(1-A) \cdot(1-B)$ (Distributive property of subtraction)
We know that, $(1-A)=\bar{A}$ and $(1-B)=\bar{B}$ (Definition of complement)
$\Rightarrow \overline{A+B}=\bar{A} \cdot \bar{B}$

2. $\overline{A \cdot B}=1-(A \cdot B)$ (Complement property)
$\quad \quad \quad=(1-A)+(1-B)$ (Distributive property of subtraction)
We know that, $(1-A)=\bar{A}$ and $(1-B)=\bar{B}$ (Definition of complement)
$\Rightarrow \overline{A \cdot B}=\bar{A}+\bar{B}$

Recommended Video Based on the De-Morgan's Law

Solved Examples Based On the De-Morgan's Law

Example 1: If $(A \cup B)=P$, then evaluate $P^{\prime}$

1) $A^{\prime} \cup B$
2) $A \cap B^{\prime}$
3) $A^{\prime} \cup B^{\prime}$
4) $A^{\prime} \cap B^{\prime}$

Solution:
Using De-Morgan's Law:

$
P^{\prime}=(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}
$

Hence, the answer is the option 4.

Example 2: Which of the following is not a property of a union of sets?

1) $A \cup(B \cup C)=(A \cup B) \cup C$

2) $A \cup B=B \cup A$
3) $(A \cup B)^c=A^c \cup B^c$
4) $(A \cap B)^c=A^c \cup B^c$

Solution:
As we learned
UNION OF SETS -
Let $A$ and $B$ be any two sets. The union of $A$ and $B$ is the set which consists of all the elements of $A$ and all the elements of $B$, the common elements being taken only once. The symbol ' $u$ ' is used to denote the union.

Symbolically, we write $A \cup B=\{x: x \in A$ or $x \in B\}$.
De Morgans's Law -
$(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}$
Hence, option 3 is incorrect.
Hence, the answer is the option 3.

Example 3: If $(A \cap B \cap C)=P$. Then evaluate $P^{\prime}$

1) $A^{\prime} \cap B^{\prime} \cap C^{\prime}$
2) $A^{\prime} \cup B^{\prime} \cup C^{\prime}$
3) $A^{\prime} \cup B^{\prime} \cap C^{\prime}$
4) $A^{\prime} \cup B^{\prime} \cap C^{\prime}$

Solution:

$
\begin{aligned}
& \mathrm{P}^{\prime}=(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})^{\prime} \\
& =((\mathrm{A} \cap \mathrm{B}) \cap \mathrm{C})^{\prime} \\
& =(\mathrm{A} \cap \mathrm{B})^{\prime} \cup \mathrm{C}^{\prime} \ldots--\{\text { De-Morgans Law }\} \\
& =A^{\prime} \cup B^{\prime} \cup C^{\prime}
\end{aligned}
$

Hence, the answer is the option 2.

Example 4: If the set $A^{\prime}=\{3,5,7\}$ and $B^{\prime}=\{1,5,9\}$, then the set $(A \cup B)^{\prime}=$
1) $\{1,3,5,7,9\}$
2) $\{5,7\}$
3) $\{5\}$
4) $\{1,5,9\}$

Solution:
As we learned
De Morgans's Law:

$
(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}
$

The intersection of $\mathrm{A}^{\prime}$ and $\mathrm{B}^{\prime}$ is $\{5\}$.
Hence, the answer is the option 3.

Example 5: If $A-B=X$ and $A-C=Y$. then the simplification of $A-(B \cup C)$ is
1) $X \cap Y$
2) $X \cup Y$
3) $X-Y$
4) $Y-X$

Solution:
As we have learned,

$
P-Q=P \cap Q^{\prime}
$

So,

$
\begin{aligned}
& A-(B \cup C)=A \cap(B \cup C)^{\prime} \\
& A \cap\left(B^{\prime} \cap C^{\prime}\right)=\left(A \cap B^{\prime}\right) \cap\left(A \cap C^{\prime}\right)=(A-B) \cap(A-C) \\
& X \cap Y
\end{aligned}
$

Hence, the answer is the option 1.

List of Topics Related to De Morgan's Law