Definite Integral - Calculus

Definite integral as the limit of a sum is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These concepts of integration have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Definite integral as the limit of a sum
2. Solved Example Based on Definite integral as the limit of a sum:
3. Summary

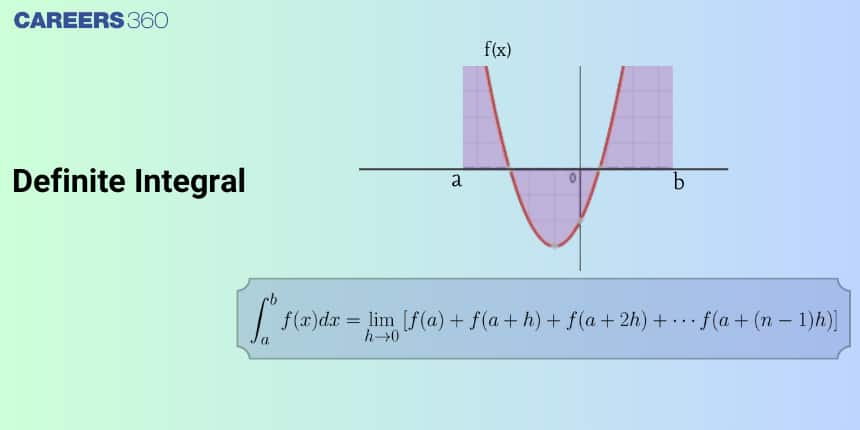
In this article, we will cover the concept of Definite integral as the limit of a sum . This concept falls under the broader category of Calculus, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), thirteen questions have been asked on this concept, including six in 2021, one in 2018, three in 2022, and four in 2023.

Definite integral as the limit of a sum

Definite integration calculates the area under a curve between two specific points on the x-axis.

Let f be a function of x defined on the closed interval [a, b] and F be another function such that $\frac{d}{d x}(F(x))=f(x)$ for all x in the domain of f, then

$\int_a^b f(x) d x=[F(x)+c]_a^b=F(b)-F(a)$is called the definite integral of the function f(x) over the interval [a, b], where a is called the lower limit of the integral and b is called the upper limit of the integral.

Let f(x) be a continuous real-valued function defined on the closed interval [a, b] which is divided into n parts as shown in the figure.

Each subinterval denoted as $\left[x_0, x_1\right],\left[x_1, x_2\right], \ldots\left[x_{i-1}, x_i\right], \ldots,\left[x_{n-1}, x_n\right]$ having equal width $\frac{b-a}{n}$ where, $x_0=a$ and $x_n=b$.

$
\Rightarrow \quad x_i-x_{i-1}=\frac{b-a}{n} \quad \text { for } i=1,2,3, \ldots, n
$
We denote the width of each subinterval with the notation $\Delta x$, so $\quad \Delta x=\frac{b-a}{n}$ and $x_i=x_0+i \Delta x$

On each subinterval,$\left.x_{i-1}, x_i\right]$ (for $\left.i=1,2,3, \ldots, n\right)$ a rectangle is constructed with width Δx and height equal to$f\left(x_{i-1}\right)$ which is the function value at the left endpoint of the subinterval. Then the area of this rectangle is s $f\left(x_{i-1}\right) \Delta x$. Adding the areas of all these rectangles, we get an approximate value for A

$\begin{aligned} A \approx L_n & =f\left(x_0\right) \Delta x+f\left(x_1\right) \Delta x+\cdots+f\left(x_{n-1}\right) \Delta x \\ & =\sum_{i=1}^n f\left(x_{i-1}\right) \Delta x\end{aligned}$

$\mathrm{L}_n$ to denote that this is a left-endpoint approximation of A using n subintervals.

The second method for approximating the area under a curve is the right-endpoint approximation. It is almost the same as the left-endpoint approximation, but now the heights of the rectangles are determined by the function values at the right of each subinterval.

This time the height of the rectangle is determined by the function value f(x_i) at the right endpoint of the subinterval. Then, the area of each rectangle is f(x_i)Δx and the approximation for A is given by

$\begin{aligned} A \approx R_n & =f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\cdots+f\left(x_n\right) \Delta x \\ & =\sum_{i=1}^n f\left(x_i\right) \Delta x\end{aligned}$

As $\mathrm{n} \rightarrow \infty$ strips become narrower and narrower, it is assumed that the limiting values of $L_n$ and $R_n$ are the same in both cases and the common limiting value is the required area under the curve.

Symbolically, we write

$\begin{aligned} & \lim _{n \rightarrow \infty} \mathrm{L}_n=\lim _{n \rightarrow \infty} \mathrm{R}_{\mathrm{n}}=\text { area of the region }=\int_a^b f(x) d x \\ & \int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^n f\left(x_i\right) \Delta x=\lim _{n \rightarrow \infty} \sum_{i=1}^n\left(\frac{b-a}{n}\right) f\left(a+\left(\frac{b-a}{n}\right) i\right) \\ & \text { where, } \quad \Delta x=\frac{b-a}{n} \text { and } x_i=x_0+\Delta x . i\end{aligned}$

NOTE:

1. If $\mathrm{a}=0, \mathrm{~b}=1$, then

$\int_0^1 f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=0}^{n-1} \frac{1}{n} f\left(\frac{i}{n}\right)$

2. From the definition of definite integral, we have

$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=\varphi(n)}^{\psi(n)} f\left(\frac{i}{n}\right)=\int_a^b f(x) d x$, where
(i) $\quad \Sigma$ is replaced by $\int$ sign
(ii) $\frac{i}{n}$ is replaced by $x$
(iii) $\frac{1}{n}$ is replaced by $d x$
(iv) To obtain the limits of integration, we use $\mathrm{a}=\lim _{\mathrm{n} \rightarrow \infty} \frac{\phi(\mathrm{n})}{\mathrm{n}}$ and $\mathrm{b}=\lim _{\mathrm{n} \rightarrow \infty} \frac{\psi(\mathrm{n})}{\mathrm{n}}$

For example:

$\begin{aligned} & \lim _{n \rightarrow \infty} \sum_{r=1}^{p . n} \frac{1}{n} f\left(\frac{r}{n}\right)=\int_\alpha^\beta f(x) d x \\ & \text { where, } \alpha=\lim _{n \rightarrow \infty} \frac{r}{n}=0(\text { as } r=1) \\ & \text { and } \quad \beta=\lim _{n \rightarrow \infty} \frac{r}{n}=p(\text { as } r=p n)\end{aligned}$

Recommended Video Based on Definite Integral as the Limit of a Sum

Solved Example Based on Definite integral as the limit of a sum:

Example 1: $\int_0^3\{x\} d x$

1) 2

2) 3/2

3) 4

4) 5

Solution

As we learned

Definite Integrals as the limit of a sum -

$\int_0^l f(x) d x=\lim _{x \rightarrow \infty} \sum \frac{1}{x} f\left(\frac{r}{x}\right)$

Or

$\int_a^b f(x) d x=\lim _{x \rightarrow \infty} h \sum_{r=0}^x f(a+r h)$

- wherein

Where $f(x)$ is a continuous function in $[0, l]$

Where $h=\frac{b-a}{x}$ And $f(x)$ is continuous in $[a, b]$

$\int_0^3\{x\}=\int_0^1\{x\} d x+\int_1^2\{x\} d x+\int_2^3\{x\} d x$

$=3 / 2$

Example 2: $\lim _{n \rightarrow \infty}\left[\frac{1}{n}+\frac{n}{(n+1)^2}+\frac{n}{(n+2)^2}+\ldots \ldots \ldots \ldots \ldots+\frac{n}{(2 n-1)^2}\right]$ is equal to:

1) $\frac{1}{2}$
2) 1
3) $\frac{1}{3}$
4) $\frac{1}{4}$

Solution

$\lim _{n \rightarrow \infty}\left[\frac{1}{n}+\frac{n}{(n+1)^2}+\frac{n}{(n+2)^2}+\ldots+\frac{n}{(2 n-1)^2}\right]$

$\begin{aligned} & =\lim _{n \rightarrow \infty} \sum_{r=0}^{n-1} \frac{n}{(n+r)^2}=\lim _{n \rightarrow \infty} \sum_{r=0}^{n-1} \frac{n}{n^2+2 n r+r^2} \\ & =\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{r=0}^{n-1} \frac{1}{(r / n)^2+2(r / n)+1}\end{aligned}$

$=\int_0^1 \frac{\mathrm{dx}}{(\mathrm{x}+1)^2}=\left[\frac{-1}{(\mathrm{x}+1)}\right]_0^1=\frac{1}{2}$

Hence, the answer is the option (1).

Example 3: $\left.\lim _{n \rightarrow \infty}\left(\frac{(n+1)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)+\frac{(n+2)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\ldots \ldots \ldots+\frac{(2 n)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)$ is equal to:

1) $\frac{3}{4}(2)^{\frac{4}{3}}-\frac{3}{4}$
2) $\frac{4}{3}(2)^{\frac{4}{3}}$
3) $\frac{3}{4}(2)^{\frac{4}{3}}-\frac{4}{3}$
4) $\frac{4}{3}(2)^{\frac{3}{4}}$

Solution

$\lim _{n \rightarrow \infty}\left(\frac{(n+1)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\frac{(n+2)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\ldots \ldots \ldots \ldots+\frac{(2 n)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)$

$=\lim _{n \rightarrow \infty} \frac{1}{n}\left[\left(1+\frac{1}{n}\right)^{\frac{1}{3}}+\left(1+\frac{2}{n}\right)^{\frac{1}{3}}+\ldots \ldots \ldots+\left(1+\frac{n}{n}\right)^{\frac{1}{3}}\right]$

$\begin{aligned} & =\frac{1}{n} \sum_{r=1}^n\left(1+\frac{r}{n}\right)^{\frac{1}{3}} \\ & =\int_0^1(1+x)^{\frac{1}{3}} d x=\frac{3}{4}\left(2^{\frac{4}{3}}-1\right)\end{aligned}$

Hence, the answer is option (1).

Example 4: $\lim _{n \rightarrow \infty}\left(\frac{n^2}{\left(n^2+1\right)(n+1)}+\frac{n^2}{\left(n^2+4\right)(n+2)}+\frac{n^2}{\left(n^2+9\right)(n+3)}+\ldots+\frac{n^2}{\left(n^2+n^2\right)(n+n)}\right)$

1) $\frac{\pi}{8}+\frac{1}{4} \log _e 2$
2) $\frac{\pi}{4}+\frac{1}{8} \log _e 2$
3) $\frac{\pi}{4}-\frac{1}{8} \log _{\mathrm{e}} 2$
4) $\frac{\pi}{8}+\log _c \sqrt{2}$

Solution:

$\lim _{n \rightarrow \infty}\left(\frac{n^2}{\left(n^2+1\right)(n+1)}+\frac{n^2}{\left(n^2+4\right)(n+2)}+\cdots+\frac{n^2}{\left(n^2+n^2\right)(n+n)}\right)$

$=\lim _{n \rightarrow \infty} \sum_{r=1}^n \frac{n^2}{\left(n^2+r^2\right)(n+r)}$

$=\int_0^1 \frac{1}{\left(1+x^2\right)(1+x)} d x$

$\begin{aligned} & =\frac{1}{2} \int_0^1 \frac{1}{1+x} d x+\frac{1}{2} \int_b^1 \frac{d x}{1+x^2}-\frac{1}{4} \int_0^1 \frac{2 x}{\left(1+x^2\right)} d x \\ & =\frac{1}{2}[\ln (1+x)]_0^1+\frac{1}{2}\left[\tan ^{-1} x\right]_0^1-\frac{1}{4}\left[\ln \left(1+x^2\right)\right]_0^1 \\ & =\frac{1}{2} \ln 2+\frac{\pi}{8}-\frac{1}{4} \ln 2 \\ & =\frac{\pi}{8}+\frac{1}{4} \log e^2\end{aligned}$

Hence, the answer is the option (1).

Example 5: If $\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1}}{n^{k+1}}[(n k+1)+(n k+2)+\ldots+(n k+n)$$=33 \cdot \lim _{n \rightarrow \infty} \frac{1}{n^{k+1}} \cdot\left[1^k+2^k+3^k+\ldots+n^k\right]$,

then the integral value of $k$ is equal to _______.

1) 5

2) 9

3) 8

4) 6

Solution

$\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1}}{n k+1}[n k \cdot n+1+2+\cdots+n]$

$=\lim _{\mathrm{n} \rightarrow \infty} \frac{(\mathrm{n}+1)^{\mathrm{k}-1}}{\mathrm{n}^{\mathrm{k}+1}} \cdot\left[\mathrm{n}^2 \mathrm{k}+\frac{(\mathrm{n}(\mathrm{n}+1)}{2}\right]$

$\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1} \cdot n^2\left(k+\frac{\left(1+\frac{1}{n}\right)}{2}\right)}{n k+1}$

$\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)\left(k+\frac{\left(1+\frac{1}{n}\right)}{2}\right)$

$\Rightarrow\left(k+\frac{1}{2}\right)$

RHS

$\Rightarrow \lim _{\mathrm{n} \rightarrow \infty} \frac{1}{\mathrm{nk}+1}\left(1^{\mathrm{k}}+2^{\mathrm{k}}+\cdots+\mathrm{h}^{\mathrm{k}}\right)=\frac{1}{\mathrm{k}+1}$

LHS=RHS

$\Rightarrow \mathrm{k}+\frac{1}{2}=33 \cdot \frac{1}{\mathrm{k}+1}$

$\begin{aligned} & \Rightarrow(2 k+1)(k+1)=66 \\ & \Rightarrow(k-5)(2 k+13)=0 \\ & \Rightarrow k=5 \text { or } \frac{13}{9}\end{aligned}$

Hence, the answer is the (5).

Summary

Definite integral as the limit of a sum is a powerful tool in calculus that allows us to calculate the area under a curve between two specific points. It provides a deeper understanding of mathematical ideas paramount for later developments in many scientific and engineering disciplines.