Difference of Set: Definition, Formula, Properties, Examples

The difference between the two collections is a concept that examines the presence of elements in one collection but not in another. For instance, consider two groups of employees in a company; In one group, some members participated in a mandatory training session, but the other group did not participate in it at all. Therefore, the possibilities in the second set that are not in the first set indicate the number of employees who have not experienced the training. This operation is essential for defining the specific problem and issue domains or domains that require a solution in specific sectors or segments within a broad classification.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is Difference of sets?
2. Properties of Difference of Sets
3. Symmetric Difference of Sets $(A\Delta B)$
4. Solved Examples Based On the Difference of Sets

In this article, we will cover the concept of the difference of sets. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept, including one in 2021.

What is Difference of sets?

Difference of sets is one of the fundamental operations in the concept of sets. It has various applications in concepts involving a specific category. Before looking into the concept of difference of sets, let us see what are sets.

Set

Sets are a foundational concept in mathematics, central to various fields such as statistics, geometry, and algebra. A set is simply a collection of distinct objects, considered as a whole. These objects, called elements or members of the set, can be anything: numbers, people, letters, etc. Sets are particularly useful in defining and working with groups of objects that share common properties.

It is a well-defined collection of distinct objects and it is usually denoted by capital letters A, B, C, S, U, V…...

Difference of Sets Definition

The difference of sets $A$ and $B$ in this order is the set of elements that belong to $A$ but not to B.

Symbolically, we write $A-B$ and read as "A minus B".

How to find the difference of sets?

To find the difference of sets,

1. Identify the given non-empty sets and write them in set-builder form.
2. Identify the order of difference, i.e., if to find $A-B$ or $B-A$.
3. Find the intersection of the sets $A$ and $B$.
4. Eliminate the elements of $A\cap B$ from Set $A$ to write a new set. In other words, remove the elements in $A$ that are also present in Set $B$.
5. Define the new set as $A-B$. Here, $A-B$ is the set of elements of $A$ that are not in $B$.

Now, let us look into difference of set example for better understanding.

Difference of Set Examples

1. $A=\{1,2,3,4\}$ and $B=\{4,5,6,8\}$,
then, $A-B=\{1,2,3\}$ and $B-A=\{5,6,8\}$

2. $A=\{blue,violet,green,yellow,black,white,red\}$ and $B=\{black,blue,red,grey,brown\}$, then $A-B=\{violet,green,yellow,white\}$ and $B-A=\{grey,brown\}$

3. $A=\{x:x\in \mathbf{N}$ and $x\le 10\}$ and $B=$ set of all integers greater than $-5$ and less than or equal to $5$.
Now, $A=\{1,2,3,4,5,6,7,8,9\}$ and $B=\{-4,-3,-2,-1,0,1,2,3,4,5\}$, then $A-B=\{6,7,8,9\}$ and $B-A=\{-4,-3,-2,-1,0\}$

4. $A=$ set of all even natural numbers less than $10$ and $B=\{2,4,6,8\}$. Now, $A=\{2,4,6,8\}$ and $B=\{2,4,6,8\}$, then $A-B=\varphi$ and $B-A=\varphi$

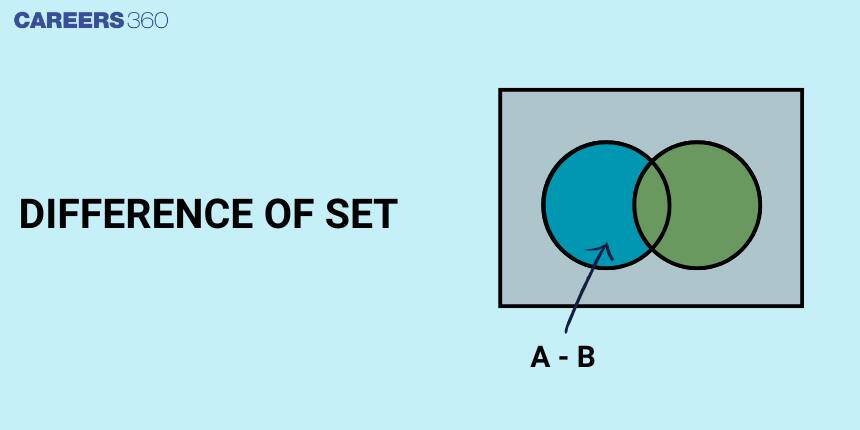
Difference of Set Venn Diagram

The difference of sets $A$ and $B$ is $A-B$. The difference of set Venn diagram is

For instance, The difference of sets venn diagram of $A=\{1,2,3,4\}$ and $B=\{4,5,6,8\}$ is

From the venn diagram, $A-B=\{1,2,3\}$ and $B-A=\{5,6,8\}$.

Properties of Difference of Sets

1. In general $A-B$ does not equal $B-A$. This means that the difference of sets are not interchangeable.

2. When we take the difference of the same set then the result is empty. (i.e) $\mathrm{A}-\mathrm{A}=\varphi$

3. When we take the difference of a finite set with the null set then the result is a finite set. (i.e) $\mathrm{A}-\varphi =\mathrm{A}$

4. When we take the difference of a finite set with a universal set then the result is empty. (i.e) $A-U=\varphi$

5. The sets $A-B,A\cap B$ and $B-A$ are mutually disjoint sets, (i.e) the intersection of any two of these sets is the null set(empty set).

Symmetric Difference of Sets $(A\Delta B)$

Symmetric difference of two sets $A$ and $B$ is defined as $A\Delta B=(A-B)\cup (B-A)$. This can also be represented as $A\Delta B=(A\cup B)-(A\cap B)$

The symmetric difference of sets can be found with the help of the following steps:

1. Identify the given non-empty sets and write them in set-builder form.
2. Now find the difference $A-B$ and $B-A$.
3. Now find the union of those sets $A-B$ and $B-A$.

Symmetric Difference of Sets Examples

1. $A=\{1,2,3,4\}$ and $B=\{4,5,6,8\}$,
then, $A-B=\{1,2,3\}$ and $B-A=\{5,6,8\}$. The symmetric difference of set are $(A-B)\cup (B-A)=\{1,2,3\}\cup \{5,6,8\}=\{1,2,3,5,6,8\}$

2. $A=\{blue,violet,green,yellow,black,white,red\}$ and $B=\{black,blue,red,grey,brown\}$, then $A-B=\{violet,green,yellow,white\}$ and $B-A=\{grey,brown\}$. The symmetric difference of set are $(A-B)\cup (B-A)=\{violet,green,yellow,white\}\cup \{grey,brown\}=\{violet,green,yellow,white,grey,brown\}$

3. $A=\{x:x\in \mathbf{N}$ and $x\le 10\}$ and $B=$ set of all integers greater than $-5$ and less than or equal to $5$.
Now, $A=\{1,2,3,4,5,6,7,8,9\}$ and $B=\{-4,-3,-2,-1,0,1,2,3,4\}$, then $A-B=\{5,6,7,8,9\}$ and $B-A=\{-4,-3,-2,-1,0\}$. The symmetric difference of set are $(A-B)\cup (B-A)=\{5,6,7,8,9\}\cup \{-4,-3,-2,-1,0\}=\{-4,-3,-2,-1,0,5,6,7,8,9\}$

4. $A=$ set of all even natural numbers less than $10$ and $B=\{2,4,6,8\}$. Now, $A=\{2,4,6,8\}$ and $B=\{2,4,6,8\}$, then $A-B=\varphi$ and $B-A=\varphi$. The symmetric difference of set are $(A-B)\cup (B-A)=\varphi \cup \varphi =\varphi$

Symmetric Difference of Set Venn Diagram

The symmetric difference of sets $A$ and $B$ is $(A-B)\cup (B-A)$. The symmetric difference of set Venn diagram is

For instance, The difference of sets venn diagram of $A=\{1,2,3,4\}$ and $B=\{4,5,6,8\}$ is

From the venn diagram, $A\Delta B=\{1,2,3,5,6,8\}$

Recommended Video Based on Difference of Sets

Solved Examples Based On the Difference of Sets

Example 1: If $\mathbf{A},\mathbf{B}$, and $\mathbf{C}$ are non-empty sets, then $(A\cup B)-(A\cap B)$
1) $(A\cup B)-B$
2) $A-(A\cap B)$
3) $(A-B)\cup (B-A)$
4) $(A\cap B)\cup (A\cup B)$

Solution:

Clearly, as the sets in the question and in the third option, both equal the symmetric difference of $A$ and $B$, so both these are equal.

$(A-B)\cup (B-A)=(A\cup B)-(A\cap B)$

Hence, the answer is the option 3.
Example 2: $\begin{array}{rl}& \mathrm{A}=\{\mathrm{n}\in \mathrm{N}\mid {\mathrm{n}}^2\le \mathrm{n}+10,000\},\mathrm{B}=\{3\mathrm{k}+1\mid \mathrm{k}\in \mathrm{N}\}\\ & C=\{2\mathrm{k}\mid \mathrm{k}\in \mathrm{N}\}A\cap (B-C)\end{array}$
$\text{ Let }\mathrm{A}=\{\mathrm{n}\in \mathrm{N}\mid {\mathrm{n}}^2\le \mathrm{n}+10,000\},\mathrm{B}=\{3\mathrm{k}+1\mid \mathrm{k}\in \mathrm{N}\}\text{ and }C=\{2\mathrm{k}\mid \mathrm{k}\in \mathrm{N}\}\text{, then the sum of all the elements of the set }A\cap (B-C)\text{ is equal to }$

Solution:

$\begin{array}{rl}& A:n^2-n\le 10,000\\ & \Rightarrow n(n-1)\le 100\cdot 100\\ & \Rightarrow n=\{1,2,\dots ,100\}\\ & B=\{4,7,10,13,\dots \}\\ & C=\{2,4,6,8,10,\dots \}\\ & B-C=\{7,13,19,\dots \}\\ & \begin{array}{r}A\cap (B-C)=\{7,13,19,\dots ,97\}\\ \text{ Sum }=\frac{16}{2}\{14+14.6\}\\ =832\end{array}\end{array}$

Hence, the answer is 832.

Example 3:

Let $\mathrm{A},\mathrm{B}$, and $\mathbf{C}$ be sets such that $\varphi \ne A\cap B\subseteq C$. Then which of the following statements is not true?
1) $B\cap C\ne \varphi$
2) If $(A-B)\subseteq C$, then $A\subseteq C$
3) $(C\cup A)\cap (C\cup B)=C$
4) If $(A-C)\subseteq B$, then $A\subseteq B$

Solution:

$\begin{array}{rl}& \text{ As }(A\cap B)\subseteq C\\ & \Rightarrow (A\cap B)\subseteq (B\cap C)\\ & \text{ as }(A\cap B)\ne {\varphi }_{\Rightarrow }(B\cap C)\ne \varphi \end{array}$
So, option (1) is true

Let $x\in A$ and $x\notin B\Rightarrow xϵ(A-B{)}_{\Rightarrow }\Rightarrow xϵC$ let $x\in A$ and $xϵB\Rightarrow xϵ(A\cap B)\Rightarrow xϵC$ Hence $x\in A$ and $x\in C\Rightarrow A\subseteq C$ So, option (2) is true.

Let

$\begin{array}{rl}& x\in C,x\in (C\cup A)\cap (C\cup B))\\ & =>xϵ(C\cup A)\text{ and }xϵ(C\cup B))\\ & (x\in C\text{ or }x\in A)\text{ and }(x\in C\text{ or }x\in B)\\ & =>xϵC\text{ or }xϵ(A\cap B)\\ & =>xϵCAs,A\cup B\subseteq C\end{array}$

$\begin{array}{rl}& (C\cup A)\cap (C\cup B)\subseteq C.......\text{ (1) }\end{array}$

Now,
$\begin{array}{rl}& =>xϵC\\ & =>xϵ(C\cup A)\cap (C\cup B)\\ & =>C\subseteq (C\cup A)\cap (C\cup B)......(2)\end{array}$

From (1) and (2)

$(C\cup A)\cap (C\cup B)=C$

=> Option (3) is correct.
For $\mathrm{A}=\mathrm{c},A-C=\varphi$

$=>\varphi \subseteq B\text{ but }=>A⊈B$
So, option (4) is not true.

Example 4:

If $A=(x\in \mathbf{R}:|x|<2)$ and $B=(x\in \mathbf{R}:|x-2|⩾3)$; then:
1) $A-B=[-1,2)$
2) $B-A=\mathbf{R}-(-2,5)$
3) $A\cup B=\mathbf{R}-(2,5)$
4) $A\cap B=(-2,-1)$

Solution:

$\begin{array}{rl}& A=\{x:x\in (-2,2)\}\\ & B=\{x:x\in (-\mathrm{\infty },-1]\cup [5,\mathrm{\infty })\}\\ & A\cap B=\{x:x\in (-2,-1]\}\\ & A\cup B=\{x:x\in (-\mathrm{\infty },2)\cup [5,\mathrm{\infty })\}\\ & A-B=\{x:x\in (-1,2)\}\\ & B-A=\{x:x\in (-\mathrm{\infty },-2]\cup [5,\mathrm{\infty })\}\end{array}$

Hence, the answer is the option 2.

List of Topics Related to Difference of Sets