Direction Cosines & Direction Ratios Of A Line

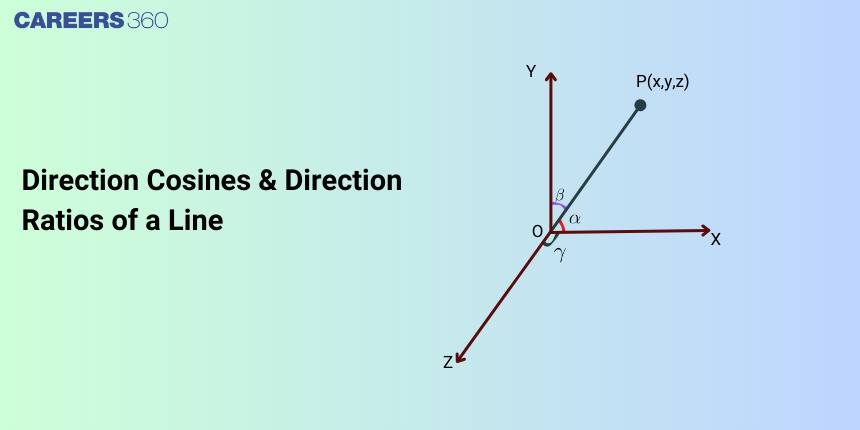
If a directed line L , passing through the origin, makes angles $\alpha, \beta$, and $\gamma$ with the ${x},{y}$ and $z$ axes, respectively, called direction angles, then the cosines of these angles, namely, $\cos (\alpha), \cos ($ $\beta) \cos (\gamma)$, are called the direction cosines of the directed line L . In real life, we use vectors for tracking the objects like airplanes and drones.

In this article, we will cover the concept of Direction Cosines and Direction Ratios of a Line. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 12 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of thirteen questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2021, two in 2022, and one in 2023.

Direction Cosines: Definition

Direction Cosine gives the relation of a vector or a line in a three-dimensional space, with each of the three axes. The direction cosine is the cosine of the angle subtended by this line with the x-axis, y-axis, and z-axis respectively. Let r be the position vector of a point P(x, y, z). Then, the direction cosines of vector r are the cosines of angles α, β, and γ (i.e. cos α, cos β, and cos γ) that the vector r makes with the positive direction of X, Y, and Z -axes respectively. Direction cosines are usually denoted by l, m, and n respectively.

$\alpha, \beta, \gamma$ are the angles that a vector makes with positive X -axis, Y -axis, and Z -axis respectively then $\cos \alpha, \cos \beta, \cos \gamma$ are known as direction cosines, generally denoted by (l,m,n).

$
\begin{aligned}
& l=\cos \alpha, m=\cos \beta, n=\cos \gamma \\
& l^2+m^2+n^2=1 \\
& \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1
\end{aligned}
$

Derivation of Direction Cosines

Let $r$ be the position vector of a point $P(x, y, z)$. Then, direction cosines of $r$ are the cosines of angles $\alpha, \beta$, and $y$ (ie. $\cos \alpha, \cos \beta$, and $\cos y)$ that the vector $r$ makes with the positive direction of $X, Y$, and $Z$-axes respectively. Direction cosines are usually denoted by $1, m$, and $n$ respectively.

A given line in space can be extended in two opposite directions, and so it has two sets of direction cosines. In order to have a unique set of direction cosines for a given line in space, we must take the given line as a directed line. These unique direction cosines are denoted by I, m, and n.

From the figure, note that $\triangle O A P$ is a right-angled triangle and thus, we have

$
\cos \alpha=\frac{x}{r}(r \text { stands for }|r|)
$
Similarly, from the right angled triangles $O B P$ and $O C P$,
We have,

$
\cos \beta=\frac{y}{r} \text { and } \cos \gamma=\frac{z}{r}
$
So we have the following results,

$
\begin{aligned}
& \cos \alpha=l=\frac{x}{\sqrt{x^2+y^2+z^2}}=\frac{x}{|\mathbf{r}|}=\frac{x}{r} \\
& \cos \beta=m=\frac{y}{\sqrt{x^2+y^2+z^2}}=\frac{y}{|\mathbf{r}|}=\frac{y}{r} \\
& \cos \gamma=n=\frac{z}{\sqrt{x^2+y^2+z^2}}=\frac{z}{|\mathbf{r}|}=\frac{z}{r}
\end{aligned}
$
We have $l^2+m^2+n^2=1$

$
\Rightarrow \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1
$
The coordinates of the point P may also be expressed as ( $\mathrm{lr}, \mathrm{mr}, \mathrm{nr})$.

Properties of Direction Cosines

i) $\sin ^2 \alpha+\sin ^2 \beta+\sin ^2 \gamma=2$
ii) If $\mathrm{OP}=\mathrm{r}$ then the co-ordinates of P will be ( $\mathrm{Ir}, \mathrm{mr}, \mathrm{nr}$ )
iii) Direction cosines of the X -axis are $(1,0,0)$
iv) Direction cosines of the $Y$-axis are $(0,1,0)$
v) Direction cosines of the Z-axis are $(0,0,1)$

Direction ratios (DRs)
Direction Ratios are any set of three numbers that are proportional to the Direction cosines.
If $\mathrm{l}, \mathrm{m}, \mathrm{n}$ are DCs of a vector then $\lambda l, \lambda m, \lambda n$ are DRs of this vector, where $\lambda$ can take any real value.
DRs are also denoted as $\mathrm{a}, \mathrm{b}$, and c respectively.
A vector has only one set of DCs, but infinite sets of DRs.
Note:
The coordinates of a point equal Ir, mr, and nr, which are proportional to the direction cosines. Hence the coordinates of a point are also its DRs.
If $\vec{r}=a i+b \hat{j}+c \hat{k}$, then $a, b$ and $c$ are one of the direction ratios of the given vector. Also, if $a^2+b^2+c^2=1$, then $a, b$ and $c$ will be direction cosines of given vector.

Properties of Directions Ratios

(i) If a, b, and c are direction ratios then direction cosines will be

$
l=\frac{ \pm a}{\sqrt{a^2+b^2+c^2}}, m=\frac{ \pm b}{\sqrt{a^2+b^2+c^2}}, n=\frac{ \pm c}{\sqrt{a^2+b^2+c^2}}
$

(ii) Direction ratios of a line joining two given points
$A\left(x_1, y_1, z_1\right)$ and $B\left(x_2, y_2, z_2\right)$ is given by

$
\left(x_2-x_1, y_2-y_1, z_2-z_1\right)
$

(iii) If $r=a \hat{i}+b \hat{j}+c \hat{k}$ be a vector with direction cosines $\mathrm{I}, \mathrm{m}, \mathrm{n}$ then

$
l=\frac{a}{|r|}, m=\frac{b}{|r|}, n=\frac{c}{|r|}
$

Direction Cosines of the Line Passing Through Two Points

Let $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1, \mathrm{z}_1\right)$ and $\mathrm{Q}\left(\mathrm{x}_2, \mathrm{y}_2, \mathrm{z}_2\right)$ be two points on the line L .
Let $1, \mathrm{~m}$, and n be the direction cosines of the line $P Q$, and let it make angles $\alpha, \beta$, and $y$ with the $x$-axis, $y$-axis, and $z$-axis respectively.
The direction cosines of the line segment joining the points $P$ and $Q$ are given by

$
\left(\frac{x_2-x_1}{P Q}, \frac{y_2-y_1}{P Q}, \frac{z_2-z_1}{P Q}\right)
$
Relationships Between Direction Cosines

If $\alpha, \beta, \gamma$ are the angles that a vector makes with positive X -axis, Y -axis, and Z -axis respectively then $\cos \alpha, \cos \beta, \cos \gamma$ are known as direction cosines, generally denoted by (l,m, n ).

$
\begin{aligned}
& l=\cos \alpha, m=\cos \beta, n=\cos \gamma \\
& l^2+m^2+n^2=1 \\
& \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1
\end{aligned}
$

Difference Between Direction Ratios and Direction Cosines

The difference between direction ratios and direction cosines is given below

Recommended Video Based on Direction Cosines & Direction Ratios of a Line

Solved Examples Based on Direction Cosines & Direction Ratios Of A Line

Example 1 : Let a unit vector $\widehat{O P}$ make angles $\alpha, \beta, \gamma_{\text {with the postive directions of the co-ordinate axes }} O X, O Y, O Z_{\text {respectively, where }} \beta \in\left(0, \frac{\pi}{2}\right)$. If $\widehat{O P}$ is perpendicular to the plane through points $(1,2,3),(2,3,4)$ and $(1,5,7)$, then which one of the following is true?
2) $\alpha \in\left(0, \frac{\pi}{2}\right)$ and $\gamma \in\left(\frac{\pi}{2}, \pi\right)$
3) $\alpha \in\left(\frac{\pi}{2}, \pi\right)$ and $\gamma \in\left(\frac{\pi}{2}, \pi\right)$
4) $\alpha \in\left(\frac{\pi}{2}, \pi\right)$ and $\gamma \in\left(0, \frac{\pi}{2}\right)$

Solution: The point on planes are $\mathrm{a}(1,2,3), \mathrm{b}(2,3,4)$ and $c(1,5,7)$

$
\begin{aligned}
& \because \overrightarrow{a b}=\langle 1,1,1\rangle \\
& \overrightarrow{a c}=\langle 0,3,4\rangle
\end{aligned}
$

the normal vector of plane $=\left[\begin{array}{ccc}\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ 1 & 1 & 1 \\ 0 & 3 & 4\end{array}\right]$

$
\begin{aligned}
& =\hat{\mathrm{i}}(1)-\hat{j}(4)+\hat{\mathrm{k}}(3) \\
& =\langle 1,-4,3\rangle
\end{aligned}
$
$
\begin{aligned}
& =\left\langle \pm \frac{1}{\sqrt{26}}, \pm \frac{4}{\sqrt{26}}, \pm \frac{3}{\sqrt{26}}\right\rangle \\
& \left(-\frac{1}{\sqrt{26}}, \frac{4}{\sqrt{26}},-\frac{3}{\sqrt{26}}\right)
\end{aligned}
$

then direction cosine of op is $\left(\because \beta \in\left(0, \frac{\pi}{2}\right)\right)$
Hence, $\alpha \in\left(\frac{\pi}{2}, \pi\right)$ and $\gamma \in\left(\frac{\pi}{2}, \pi\right)$
Hence, the answer is the option(3).

Example 2: If two straight lines whose direction cosines are given by the relations $l+\mathrm{m}-\mathrm{n}=0,3 l^2+\mathrm{m}^2+\mathrm{cn} l=0$ are parallel, then the positive value of $c$ is? [JEE MAINS 2022]

1) 6

2) 4

3) 3

4) 2

Solution: $1+\mathrm{m}=\mathrm{n}$ $\qquad$
(1) $3 \mathrm{l}^2+\mathrm{m}^2+\mathrm{cnl}=0$ $\qquad$
Substituting $\mathrm{n}=1+\mathrm{m}$ in eqn(2)

$
\begin{aligned}
& \Rightarrow \quad 3 l^2+m^2+c(1+m) l=0 \\
& \Rightarrow \quad(3+c) l^2+c m l+m^2=0 \\
& \Rightarrow \quad(3+c)\left(\frac{1}{m}\right)^2+c\left(\frac{1}{m}\right)+1=0
\end{aligned}
$
Since lines are parallel $\Rightarrow$ this quadratic will have repeated roots $\Rightarrow D=0$

$
\begin{aligned}
& \Rightarrow c^2-4(3+c)=0 \\
& \Rightarrow c^2-4 c-12=0 \Rightarrow c=6 \text { or } c=-2
\end{aligned}
$
So positive value of $\mathrm{c}=6$
Hence, the answer is the option 1.

Example 3: Let $\mathrm{p}(-2,-1,1)$ and $\mathrm{Q}\left(\frac{56}{17}, \frac{43}{17}, \frac{111}{17}\right)$ be the vertices of the rhombus PRQS. If the direction ratios of the diagonal $\mathrm{RSare} \alpha,-1, \beta$, where both $\alpha$ and $\beta$ are integers of minimum absolute values, then $\alpha^2+\beta^2$ is equal to $\qquad$
1) 450
2) 360
3) 280
4) 130

Solution

$
\mathrm{RS} \equiv(\alpha,-1, \beta)
$
DR of $\mathrm{PQ} \equiv\left(\frac{56}{17}+2, \frac{43}{17}+1, \frac{111}{17}-1\right)$

$
\begin{aligned}
& \equiv\left(\frac{90}{17}, \frac{60}{17}, \frac{24}{17}\right) \\
& \frac{90}{17} \alpha+\frac{60}{17}(-1)+\frac{94}{17} \beta=0 \\
& 90 \alpha+94 \beta=60 \\
& \beta=\frac{60-9^{\circ} \alpha}{94} \\
& \beta=\frac{30(2-3 \alpha)}{94} \\
& \beta=-30 \frac{(3 \alpha-2)}{94} \\
& \beta=\frac{-15}{47}(3 \alpha-2) \\
& \Rightarrow \frac{\beta}{75}=\frac{3 \alpha-2}{47} \\
& \Rightarrow \beta=-15, \quad \alpha=-15 \\
& \alpha^2+\beta^2=225+225=450
\end{aligned}
$
Hence, the answer is the 450.

Example 4: The angle between the straight lines, whose direction cosines are given by the equations $2 l+2 m-n=0$ and $m n+n l+l m=0$, is :
[JEE MAINS 20
1) $\pi-\cos ^{-1}\left(\frac{4}{9}\right)$
2) $\frac{\pi}{2}$
3) $\cos ^{-1}\left(\frac{8}{9}\right)$
4) $\frac{\pi}{3}$

Solution: $2 l+2 m-n=0$
$\Rightarrow n=2 l+2 m$
$m n+n l+l m=0$
$\Rightarrow n(m+l)+l m=0$
$\Rightarrow 2(l+m)(l+m)+l m=0$
$\Rightarrow 2 l^2+4 m l+2 m^2+l m=0$
$\Rightarrow 2 l(l+2 m)+m(l+2 m)=0$
$\Rightarrow(2 l+m)(l+2 m)=0$
$\Rightarrow m=-2 l$ or $l=-2 m$
From (1) and (2)

$
\begin{aligned}
n & =2 l+2 m \\
& =2 l-4 l=-2 l \text { or }-4 m+2 m=-2 m
\end{aligned}
$
So $m=-2 l=n$ OR $l=-2 m=n$
Also $l^2+m^2+n^2=1$

$
\Rightarrow l^2+4 l^2+4 l^2-1 \Rightarrow l= \pm \frac{1}{3}
$

$O R 4 m^2+m^2+4 m^2=1 \Rightarrow m=\frac{1}{3}$
$
\text { So } L_1: \pm\left(\frac{1}{3}, \frac{-2}{3}, \frac{-2}{3}\right) L_2: \pm\left(\frac{-2}{3}, \frac{1}{3}, \frac{-2}{3}\right)
$
Angle

$
\begin{aligned}
\cos \theta & =\left|l_1 l_2+m_1 m_2+n_1 n_2\right| \\
& =\left|\frac{-2}{9}-\frac{2}{9}+\frac{4}{9}\right|=0 \\
& \Rightarrow \theta=90^{\circ}=\frac{\pi}{2}
\end{aligned}
$
Hence, the answer is the option 2.

Example 5: A vector makes angles $\frac{\pi}{3}, \frac{\pi}{6}, \frac{\pi}{2}$ with positive $x, y$, and $z$ axes respectively, then it has one of the direction ratios as
1) $-2, \sqrt{3}, 1$
2) $2,-\sqrt{3}, 0$
3) $\sqrt{3}, 2,0$
4) $-1,-\sqrt{3}, 0$

Solution: $l=\cos \frac{\pi}{3}=\frac{1}{2} ; m=\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2} ; n=\cos \frac{\pi}{2}=0$
Multiplying these Direction cosines by ( -2 ), we get one of the DRs of the vector, which gives us $-1,-\sqrt{3}, 0$
Hence, the answer is the option 4.

Summary

Direction cosines are essential mathematical representations for describing the orientation of vectors in three-dimensional space. By defining the cosines of angles between vectors and coordinate axes, they offer a standardized method to specify direction independently of magnitude. Understanding of Direction cosines helps us to analyze and solve different varieties of Problems.