Dot Product of Two Vectors - Properties and Examples

Multiplication (or product) of two vectors is defined in two ways, namely, dot (or scalar) product where the result is a scalar, and vector (or cross) product where the result is a vector. Based on these two types of products for vectors, we have various applications in geometry, mechanics, and engineering. In real life, we use dot product when installing a solar panel on a roof.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is a Dot (scalar) Product?
2. Dot Product of two vector
3. Derivation of Dot Product
4. Properties of Dot (Scalar) Product
5. The angle between two vectors
6. Geometrical Interpretation of Scalar Product
7. Working Rule to Find The Dot Product of Two Vectors
8. Dot Product of Unit Vectors
9. Solved Examples on Dot (Scalar) Product of Two Vectors

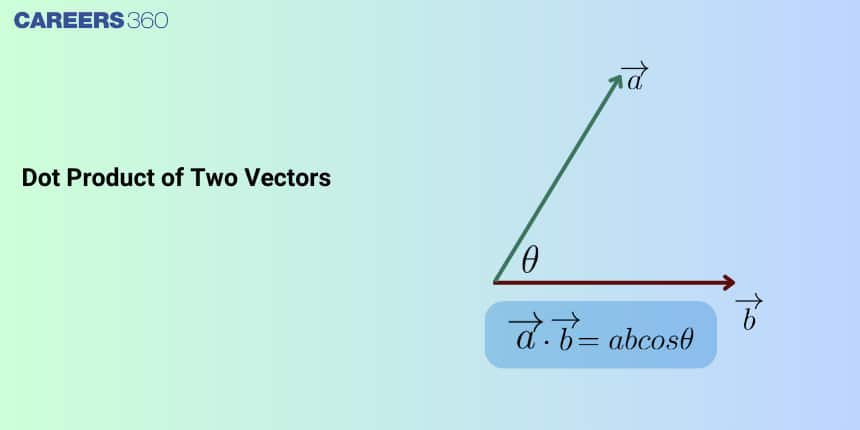
In this article, we will cover the concept of Dot Product Of Two Vectors. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of fourty five questions have been asked on this topic in JEE Main from 2013 to 2023 including two in 2021.

What is a Dot (scalar) Product?

The dot product of two vectors is the product of the magnitude of the two vectors and the cos of the angle between them.

If $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ are two non-zero vectors, then their scalar product (or dot product) is denoted by $\overrightarrow{\mathrm{a}}\cdot \overrightarrow{\mathrm{b}}$
Dot Product: Formula
If $\overrightarrow{a}$ and $\overrightarrow{\mathrm{b}}$ are two non-zero vectors, then their scalar product (or dot product) is denoted by $\overrightarrow{a}\cdot \overrightarrow{b}$
$\overrightarrow{\mathrm{a}}\cdot \overrightarrow{\mathrm{b}}=|\overrightarrow{\mathrm{a}}||\overrightarrow{\mathrm{b}}|\cos \theta (0\le \theta \le \pi )$ where $\theta$ is the angle between $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$

Observations:

1. $\overrightarrow{a}\cdot \overrightarrow{b}$ is a real number.
2. $\overrightarrow{a}\cdot \overrightarrow{b}$ is positive if $\theta$ is acute.
3. $\overrightarrow{a}\cdot \overrightarrow{b}$ is negative if $\theta$ is obtuse.
4. $\overrightarrow{a}\cdot \overrightarrow{b}$ is zero if $\theta$ is ${90}^{\circ }$.
5. $\overrightarrow{a}\cdot \overrightarrow{b}\le |\overrightarrow{a}||\overrightarrow{b}|$

Dot Product of two vector

If $\overrightarrow{\mathbf{a}}=a_1\hat{\mathbf{i}}+a_2\hat{\mathbf{j}}+a_3\hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{b}}=b_1\hat{\mathbf{i}}+b_2\hat{\mathbf{j}}+b_3\hat{\mathbf{k}}$, then $\mathbf{a}\cdot \mathbf{b}=a_1{b}_1+a_2{b}_2+a_3{b}_3$

Derivation of Dot Product

$\begin{array}{rl}\overrightarrow{a}\cdot \overrightarrow{b}=& (a_1\hat{i}+a_2\hat{j}+a_3\hat{k})\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})\\ =& a_1\hat{i}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_2\hat{j}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_3\hat{k}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})\\ =& a_1{b}_1(\hat{i}\cdot \hat{i})+a_1{b}_2(\hat{i}\cdot \hat{j})+a_1{b}_3(\hat{i}\cdot \hat{k})+a_2{b}_1(\hat{j}\cdot \hat{i})+a_2{b}_2(\hat{j}\cdot \hat{j})+a_2{b}_3(\hat{j}\cdot \hat{k})\\ & +a_3{b}_1(\hat{k}\cdot \hat{i})+a_3{b}_2(\hat{k}\cdot \hat{j})+a_3{b}_3(\hat{k}\cdot \hat{k})\\ =& a_1{b}_1+a_2{b}_2+a_3{b}_3\end{array}$

Properties of Dot (Scalar) Product

1. $\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}}\cdot \overrightarrow{\mathbf{a}}$ (commutative)
2. $\overrightarrow{a}\cdot (\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\cdot \overrightarrow{c}+\overrightarrow{a}\cdot \overrightarrow{c}$
(distributive )
3. $(m\overrightarrow{\mathbf{a}})\cdot \overrightarrow{\mathbf{b}}=m(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}})=\overrightarrow{\mathbf{a}}\cdot (m\overrightarrow{\mathbf{b}})$; where $m$ is a scalar and $\overrightarrow{a},\overrightarrow{b}$ are any two vectors
4. $(l\overrightarrow{\mathbf{a}})\cdot (\mathrm{m}\overrightarrow{\mathbf{b}})=\mathrm{lm}(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}})$; where $l$ and $m$ are scalars

For any two vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, we have
(I)

$\begin{array}{rl}|\overrightarrow{a}\pm \overrightarrow{b}{|}^2& =|\overrightarrow{a}\pm \overrightarrow{b}|\cdot |\overrightarrow{a}\pm \overrightarrow{b}|\\ & =|\overrightarrow{a}{|}^2+|\overrightarrow{b}{|}^2\pm 2\overrightarrow{a}\cdot \overrightarrow{b}\\ & =|\overrightarrow{a}{|}^2+|\overrightarrow{b}{|}^2\pm 2|\overrightarrow{a}||\overrightarrow{b}|\cos \theta \end{array}$

(ii) $|\overrightarrow{a}+\overrightarrow{b}|\cdot |\overrightarrow{a}-\overrightarrow{b}|=|\overrightarrow{a}{|}^2-|\overrightarrow{b}{|}^2$
(iii) $|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|+|\overrightarrow{b}|\Rightarrow \overrightarrow{a}$ and $\overrightarrow{b}$ are like vectors
(iv) $|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}-\overrightarrow{b}|\Rightarrow \overrightarrow{a}\perp \overrightarrow{b}$

The angle between two vectors

The angle between two vectors is calculated as the cosine of the angle between the two vectors. The cosine of the angle between two vectors is equal to the sum of the products of the individual constituents of the two vectors, divided by the product of the magnitude of the two vectors. The formula for the angle between the two vectors is given by

$\begin{array}{rl}& \overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}=|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|\cos \theta \\ & \Rightarrow \cos \theta =\frac{\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}\\ & \Rightarrow \theta ={\cos }^{-1}\left(\frac{\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{a}}||\overrightarrow{\mathbf{b}}|}\right)\\ & \text{ If }\overrightarrow{\mathbf{a}}=a_1\hat{\mathbf{i}}+a_2\hat{\mathbf{j}}+a_3\hat{\mathbf{k}}\text{ and }\overrightarrow{\mathbf{b}}=b_1\hat{\mathbf{i}}+b_2\hat{\mathbf{j}}+b_3\hat{\mathbf{k}}\\ & \Rightarrow \theta ={\cos }^{-1}\left(\frac{a_1{b}_1+a_2{b}_2+a_3{b}_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}\right)\end{array}$

Geometrical Interpretation of Scalar Product

The dot product of two vectors is constructed by taking the component of one vector in the direction of the other and multiplying it with the magnitude of the other vector. To understand the vector dot product, we first need to know how to find the magnitude of two vectors, and the angle between two vectors to find the projection of one vector over another vector.

Magnitude of A Vector

A vector represents a direction and a magnitude. The magnitude of a vector is the square root of the sum of the squares of the individual constituents of the vector. The magnitude of a vector is a positive quantity.

For a vector, $\overrightarrow{OP}=\widehat{xi}+y\hat{j}+z\hat{k}$ its magnitude is given by $\overrightarrow{OP}\mid =\sqrt{x^2+y^2+z^2}=r$

Projection of a Vector

The dot product is useful for finding the component of one vector in the direction of the other. The resultant of a vector projection formula is a scalar value.

Let $\overrightarrow{a}$ and $\overrightarrow{b}$ be two vectors represented by OA and OB, respectively.

Draw $\mathrm{BL}\perp \mathrm{OA}$ and $\mathrm{AM}\perp \mathrm{OB}$.
From triangles $OBL$ and $OAM$ we have $OL=OB\cos \theta$ and $OM=OA\cos \theta$.
Here OL and OM are known as projections of $\overrightarrow{\mathbf{b}}$ on $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{a}}$ on $\overrightarrow{\mathbf{b}}$ respectively.

Now, $\begin{array}{rl}\overrightarrow{a}\cdot \overrightarrow{b}& =|\overrightarrow{a}||\overrightarrow{b}|\cos \theta \\ & =|\overrightarrow{a}|(OB\cos \theta )\\ & =|\overrightarrow{a}|(OL)\\ & =(\text{ magnitude of }\overrightarrow{a})(\text{ projection of }\overrightarrow{b}\text{ on }\overrightarrow{a})\\ \text{ Again, }\overrightarrow{a}\cdot \overrightarrow{b}& =|\overrightarrow{a}||\overrightarrow{b}|\cos \theta \\ & =|\overrightarrow{b}|(|\overrightarrow{a}|\cos \theta )\\ & =|\overrightarrow{b}|(OA\cos \theta )\\ & =|\overrightarrow{b}|(OM)\\ & =(\text{ magnitude of }\overrightarrow{b})\text{ ( projection of }\overrightarrow{a}\text{ on }\overrightarrow{b}\end{array}$

Thus. geometrically interpreted, the scalar product of two vectors is the product of the modulus of either vector and the projection of the other in its direction.

Thus,

Projection of $\overrightarrow{\mathbf{a}}$ on $\overrightarrow{\mathbf{b}}=\frac{\overrightarrow{\mathrm{a}}\cdot \overrightarrow{\mathbf{b}}}{|\overrightarrow{\mathbf{b}}|}=\overrightarrow{\mathbf{a}}\cdot \frac{\overrightarrow{\mathrm{b}}}{|\overrightarrow{\mathbf{b}}|}=\overrightarrow{\mathbf{a}}\cdot \hat{\mathbf{b}}$ Projection of $\overrightarrow{b}$ on $\overrightarrow{a}=\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{|\overrightarrow{a}|}=\overrightarrow{b}\cdot \frac{\overrightarrow{a}}{|\overrightarrow{a}|}=\overrightarrow{b}\cdot \hat{a}$

Working Rule to Find The Dot Product of Two Vectors

If the two vectors are expressed in terms of unit vectors, i, j, k, along the x, y, and z axes, then the scalar product is obtained as follows:

$\begin{array}{rl}\overrightarrow{a}\cdot \overrightarrow{b}=& (a_1\hat{i}+a_2\hat{j}+a_3\hat{k})\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})\\ =& a_1\hat{i}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_2\hat{j}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_3\hat{k}\cdot (b_1\hat{i}+b_2\hat{j}+b_3\hat{k})\\ =& a_1{b}_1(\hat{i}\cdot \hat{i})+a_1{b}_2(\hat{i}\cdot \hat{j})+a_1{b}_3(\hat{i}\cdot \hat{k})+a_2{b}_1(\hat{j}\cdot \hat{i})+a_2{b}_2(\hat{j}\cdot \hat{j})+a_2{b}_3(\hat{j}\cdot \hat{k})\\ & +a_3{b}_1(\hat{k}\cdot \hat{i})+a_3{b}_2(\hat{k}\cdot \hat{j})+a_3{b}_3(\hat{k}\cdot \hat{k})\\ =& a_1{b}_1+a_2{b}_2+a_3{b}_3\end{array}$

Dot Product of Unit Vectors

For any two non-zero vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, then $\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}=0$ if and only if $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ perpendicular to each other. i.e.
$\overrightarrow{a}\cdot \overrightarrow{b}=0\iff \overrightarrow{a}\perp \overrightarrow{b}$
As $\hat{\mathbf{i}},\hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are mutually perpendicular unit vectors along the coordinate axes, therefore,

$\hat{\mathbf{i}}\cdot \hat{\mathbf{j}}=\hat{\mathbf{j}}\cdot \hat{\mathbf{i}}=0,\hat{\mathbf{j}}\cdot \hat{\mathbf{k}}=\hat{\mathbf{k}}\cdot \hat{\mathbf{j}}=0;\hat{\mathbf{k}}\cdot \hat{\mathbf{i}}=\hat{\mathbf{i}}\cdot \hat{\mathbf{k}}=0$

If $\theta =0$, then $\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}}=|\overrightarrow{a}||\overrightarrow{b}|$
In particular, $\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{a}}=|\overrightarrow{\mathbf{a}}{|}^2$
As $\hat{\mathbf{i}},\hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are unit vectors along the coordinate axes, therefore $\hat{\mathbf{i}}\cdot \hat{\mathbf{i}}=|\hat{\mathbf{i}}{|}^2=1,\hat{\mathbf{j}}\cdot \hat{\mathbf{j}}=|\hat{\mathbf{j}}{|}^2=1$ and $\hat{\mathbf{k}}\cdot \hat{\mathbf{k}}=|\hat{\mathbf{k}}{|}^2=1$

Recommended Videos Based on Dot Product of Two Vectors

Solved Examples on Dot (Scalar) Product of Two Vectors

Example 1: Let S be the set of all $\mathrm{a}\in \mathbb{R}$ for which the angle between the vectors $\overrightarrow{u}=\mathrm{a}({\log }_e\mathrm{b})\hat{\mathrm{i}}-6\hat{\mathrm{j}}+3\hat{\mathrm{k}}\overrightarrow{v}=({\log }_e\mathrm{b})\hat{\mathrm{i}}+2\hat{\mathrm{j}}+2\mathrm{a}({\log }_e\mathrm{b})\hat{\mathrm{k}},(\mathrm{b}>1)$ is acute. Then S is equal to:
Solution
$\tilde{\mathrm{u}}\cdot \tilde{\mathrm{v}}=\mathrm{a}(\log \mathrm{b}{)}^2-12+6\mathrm{a}(\log \mathrm{b})>0$
For $\mathrm{b}>1\Rightarrow \log \mathrm{b}>0$
$\tilde{\mathrm{u}}\cdot \hat{\mathrm{v}}=\mathrm{a}(\log \mathrm{b}{)}^2-12+6\mathrm{a}(\log \mathrm{b})>0$
Let $\log \mathrm{b}=\mathrm{t}\Rightarrow \mathrm{t}>0$
For $\mathrm{b}>1\Rightarrow \log \mathrm{b}>0$
$\Rightarrow {\mathrm{at}}^2+6\mathrm{at}-12>0$ for all $\mathrm{t}>0$ But fort $=0\Rightarrow \mathrm{f}(\mathrm{t})=-12$ Let $\log \mathrm{b}=\mathrm{t}\Rightarrow \mathrm{t}>0$
$\therefore a{t}^2+6at-12$ cannot be positive for all $t>0$ for any value of $a\Rightarrow a{t}^2+6at-12>0$ for all $t>0$ But fort $=0\Rightarrow f(t)=-12$
$\therefore$ option (B)
$\therefore {\mathrm{at}}^2+6$ at -12 cannot be positive for all $\mathrm{t}>0$ for any value of a
Hence, the answer is $\mathrm{\Phi }$

Example 2: Let a vector $\overrightarrow{a}$ has magnitude 9. Let a vector $\overrightarrow{b}$ be such that for every $(\mathrm{x},\mathrm{y})\in \mathbf{R}\times \mathbf{R}-\{(0,0)\}$, the vector $(\mathrm{x}\overrightarrow{a}+\mathrm{y}\overrightarrow{b})$ is perpendicular to the vector $(6\mathrm{y}\overrightarrow{a}-18\mathrm{x}\overrightarrow{b})$. Then the value of $|\overrightarrow{a}\times \overrightarrow{b}|$ is equal to:
[JEE MAINS 2022]
Solution

$\begin{array}{rl}& |\tilde{a}|=9\mathrm{\&}(x\tilde{a}+y\overline{b})\cdot (6yã-18x\overline{b})=0\\ & \Rightarrow 6xy|\tilde{a}{|}^2-18x^2(\tilde{a}\cdot \overline{b})+6y^2(\tilde{a}\cdot \overline{b})-{|8xy|\overline{b}|}^2=0\\ & \Rightarrow 6xy(|\tilde{a}{|}^2-3|\tilde{b}{|}^2)+(\tilde{a}\cdot \tilde{b})(y^2-3x^2)=0\end{array}$
$\begin{array}{rl}& \therefore |\tilde{\mathrm{a}}{|}^2=3|\tilde{b}{|}^2\mathrm{\&}(\tilde{\mathrm{a}}\cdot \tilde{\mathrm{b}})=0\\ & \begin{array}{rl}\text{ Now }|\tilde{\mathrm{a}}\times \tilde{\mathrm{b}}{|}^2& =|\tilde{\mathrm{a}}{|}^2|\tilde{b}{|}^2-(\tilde{a}\cdot \tilde{b}{)}^2\\ & =|\tilde{a}{|}^2\cdot \frac{|\tilde{a}{|}^2}{3}\end{array}\end{array}$
This should hold $\mathrm{\forall }\mathbf{x},\mathbf{y}\in \mathrm{RXR}\therefore |\tilde{\mathrm{a}}\times \tilde{\mathrm{b}}|=\frac{|\tilde{\mathrm{a}}{|}^2}{\sqrt{2}}=\frac{81}{\sqrt{3}}=27\sqrt{3}$
Hence, the answer is $27\sqrt{3}$
3

Example 3: In a triangle ABC , if $|\overrightarrow{\mathrm{BC}}|=3,|\overrightarrow{\mathrm{CA}}|=5$ and $|\overrightarrow{\mathrm{BA}}|=7$, then the projection of the vector $\overrightarrow{\mathrm{BA}}$ on $\overrightarrow{\mathrm{BC}}$ is equal to [JEE MAINS 2021]

Solution

Clearly projection of AB on BC is $|\overrightarrow{AB}|\cos B=7\cos B$
To get $\cos B$ we can apply Casine Rule

$\begin{array}{rl}\cos B=\frac{a^2+c^2-b^2}{2ac}& =\frac{9+49-25}{2(3)(7)}\\ & =\frac{33}{2.3.7}=\frac{11}{14}\\ \therefore \text{ Projection }& =7\cdot \frac{11}{14}=\frac{11}{2}\end{array}$
Hence, the correct option is $\frac{11}{2}$