Vector Algebra - Notes, Types, Formula, Books, FAQs

Vector Algebra in Mathematics

Vector Algebra plays a key role in representing and analysing quantities that have both magnitude and direction in mathematics. It provides powerful tools to solve problems related to geometry, motion, and force in a clear and systematic manner.

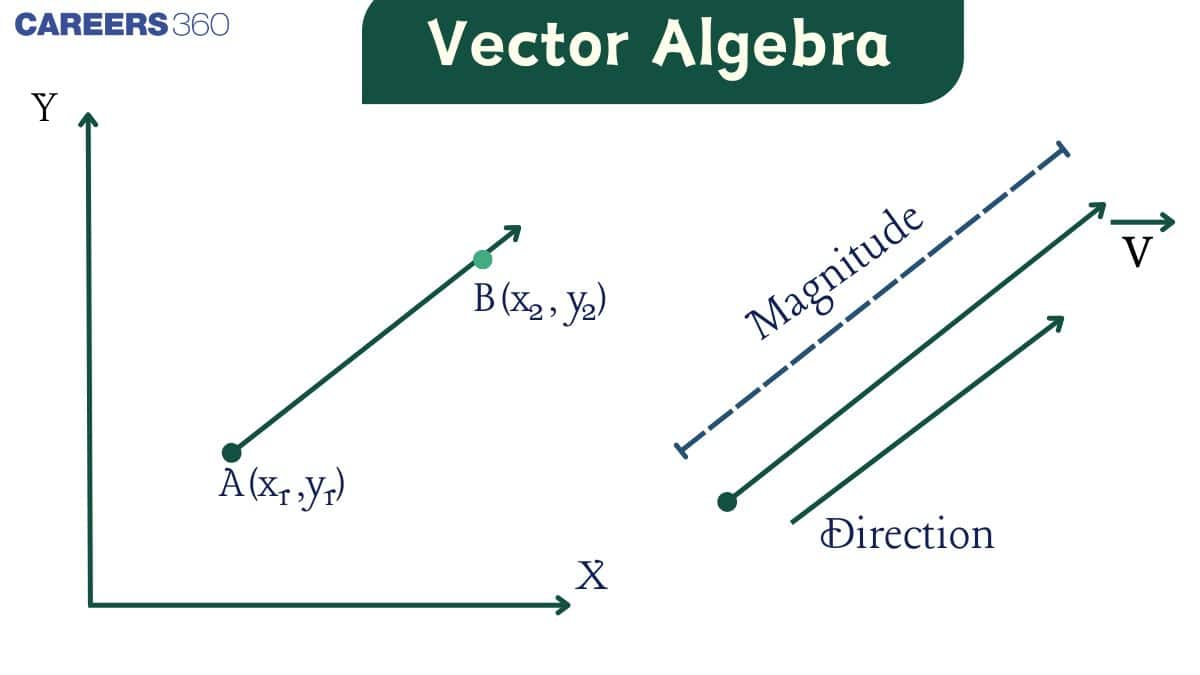
Vector- In general terms, a vector is defined as an object having both direction as well as magnitude.

Position vector- Consider a point $P$ in space, having coordinates $(x, y, z)$ with respect to the origin $\mathrm{O}(0,0,0)$. Then, the vector $\overrightarrow{O P}($ or $\vec{r})$ having $O$ and $P$ as its initial and terminal points, respectively, is called the position vector of the point $P$ with respect to $O$.

Types of vectors

The types of vectors are,

Zero Vector: A vector whose initial and terminal points coincide is called a zero vector (or null vector). A zero vector can not be assigned a definite direction as it has zero magnitude. Alternatively, it may be regarded as having any direction. The vector $\overrightarrow{A A}$ or $\overrightarrow{B B}$ represents the zero vector.

Unit Vector: A vector whose magnitude is unity (i.e., $1$ unit) is called a unit vector. The unit vector in the direction of a given vector $\vec{a}$ is denoted by $\hat{a}$.

Coinitial Vectors: Two or more vectors having the same initial point are called coinitial Vectors.

Collinear Vectors: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.

Equal Vectors: Two vectors $\vec{a}$ and $\vec{b}$ are said to be equal if they have the same magnitude and direction, regardless of the positions of their initial points, and written as $\vec{a}=\vec{b}$.

Negative of a Vector: A vector whose magnitude is the same as that of a given vector (say, $\overrightarrow{A B}$ ), but whose direction is opposite to that of it, is called the negative of the given vector.

Component Form of Vector

If a vector is represented as $x \hat{i}+y \hat{j}+z \hat{k}$, then it is called the component form of the vector. Here, $\hat{i}, \hat{j}$ and $\hat{k}$ representing the unit vectors along the
$x, y$, and $z$-axes, respectively and $(x, y, z)$ represent coordinates of the vector.
Some important points:
If $\vec{a}$ and $\vec{b}$ are any two vectors given in the component form $a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$, respectively, then,
The resultant of the vectors is

$
(\vec{a} \pm \vec{b})=\left(a_1 \pm b_1\right) \hat{i}+\left(a_2 \pm b_2\right) \hat{j}+\left(a_3 \pm b_3\right) \hat{k}
$

The vectors are equal if and only if

$
a_1=b_1, a_2=b_2 \text { and } a_3=b_3
$

The multiplication of vector $\vec{a}$ by any scalar $\lambda$ is given by

$
\lambda \vec{a}=\lambda a_1 \hat{i}+\lambda a_2 \hat{j}+\lambda a_3 \hat{k}
$

Section Formula

When point $R$ divides $\vec{PQ}$ internally in the ratio of $m:n$ such that $\frac{\overrightarrow{P R}}{\overrightarrow{R Q}}=\frac{m}{n} \quad \vec{r}=\frac{m \vec{b}+n \vec{a}}{m+n}$.
When point $R$ divides $\overrightarrow{P Q}$ externally in the ratio of $m:n$ such that $\frac{\overrightarrow{P R}}{\overrightarrow{Q R}}=\frac{m}{n} \vec{r}_{\text {then }}=\frac{m \vec{b}-n \vec{a}}{m-n}$.

Product of two vectors

Multiplication of two vectors is defined in two ways:
(i) Scalar (or dot) product and (ii) Vector (or cross) product.

In the scalar product, the resultant is a scalar quantity.
In the vector product, the resultant is a vector quantity.

Scalar product
Scalar product, also known as the dot product of two non-zero vectors $\vec{a}$ and $\vec{b}$, is denoted by $\vec{a} \cdot \vec{b}$. Scalar product is calculated as $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$ where, $\theta$ is the angle between two non zero given vectors.

Vector product
Vector product of two non-zero vectors $\vec{a}$ and $\vec{b}$ is denoted by $\vec{a} \times \vec{b}$. Vector product also known as cross product can be calculated as $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n} \quad$ where $\theta$ is the angle between two non zero vectors and $\hat{n}$ is a unit vector perpendicular to both.

Vector Operations

In vector algebra class 12, vectors are combined and manipulated using various operations. These operations are essential in solving problems in class 12 vector algebra and are widely used in physics, engineering, and mathematics. The main operations include:

1. Vector Addition

The sum of two vectors $\vec{A}$ and $\vec{B}$ is a vector $\vec{R}$ obtained by placing them tip-to-tail or using components:
$
\vec{R} = \vec{A} + \vec{B} = (A_x + B_x)\hat{i} + (A_y + B_y)\hat{j} + (A_z + B_z)\hat{k}
$

2. Vector Subtraction

The difference between two vectors $\vec{A}$ and $\vec{B}$ is:
$
\vec{D} = \vec{A} - \vec{B} = (A_x - B_x)\hat{i} + (A_y - B_y)\hat{j} + (A_z - B_z)\hat{k}
$

3. Scalar Multiplication

A vector can be multiplied by a scalar $k$, which scales its magnitude without changing its direction:
$
\vec{R} = k \vec{A} = k A_x \hat{i} + k A_y \hat{j} + k A_z \hat{k}
$

4. Dot Product (Scalar Product)

The dot product of two vectors $\vec{A}$ and $\vec{B}$ gives a scalar and is defined as:
$
\vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos \theta
$
where $\theta$ is the angle between $\vec{A}$ and $\vec{B}$. Using components:
$
\vec{A} \cdot \vec{B} = A_x B_x + A_y B_y + A_z B_z
$

5. Cross Product (Vector Product)

The cross product of two vectors $\vec{A}$ and $\vec{B}$ results in a vector perpendicular to both, with magnitude:
$
|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin \theta
$
and direction given by the right-hand rule. In component form:
$
\vec{A} \times \vec{B} =
\begin{vmatrix}
\hat{i} & \hat{j} & \hat{k} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{vmatrix}
$

These operations form the foundation for vector algebra class 12 solutions and are used in calculating displacement, force, and motion problems in class 12 vector algebra.

Class 12 Vector Algebra Formulae

In class 12 vector algebra, understanding key formulas is essential for solving problems effectively. Here are the main formulas with their definitions and applications:

1. Magnitude of a Vector

The magnitude (or length) of a vector $\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$ is the distance from the origin to the point it represents:
$
|\vec{A}| = \sqrt{A_x^2 + A_y^2 + A_z^2}
$

2. Unit Vector

A unit vector has a magnitude of 1 and points in the direction of a vector $\vec{A}$. It is given by:
$
\hat{A} = \frac{\vec{A}}{|\vec{A}|}
$

3. Direction Ratios and Direction Cosines

For a vector $\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$, the direction cosines $(\cos \alpha, \cos \beta, \cos \gamma)$ are:
$
\cos \alpha = \frac{A_x}{|\vec{A}|}, \quad \cos \beta = \frac{A_y}{|\vec{A}|}, \quad \cos \gamma = \frac{A_z}{|\vec{A}|}
$
The numbers proportional to $A_x, A_y, A_z$ are called direction ratios.

4. Dot Product Formulas

The dot product of $\vec{A}$ and $\vec{B}$ measures how much one vector extends in the direction of another:
$
\vec{A} \cdot \vec{B} = |\vec{A}| |\vec{B}| \cos \theta = A_x B_x + A_y B_y + A_z B_z
$

5. Cross Product Formulas

The cross product gives a vector perpendicular to both $\vec{A}$ and $\vec{B}$:

Magnitude:
$
|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin \theta
$

Direction: Right-hand rule

Component form:
$
\vec{A} \times \vec{B} =
\begin{vmatrix}
\hat{i} & \hat{j} & \hat{k} \
A_x & A_y & A_z \
B_x & B_y & B_z
\end{vmatrix}
$

Applications: Area of a parallelogram = $|\vec{A} \times \vec{B}|$, volume of parallelepiped = $|\vec{A} \cdot (\vec{B} \times \vec{C})|$

6. Triple Scalar Product

The triple scalar product gives the volume of a parallelepiped formed by vectors $\vec{A}, \vec{B}, \vec{C}$:
$
V = \vec{A} \cdot (\vec{B} \times \vec{C})
$
If $V = 0$, the vectors are coplanar.

This section provides all essential vector algebra class 12 formulas needed to solve NCERT and board exam problems efficiently.

Important Formulae for Vector Algebra

Given below is the list of important formulae related to vector algebra, which help in solving a variety of problems related to vectors:

Vector Algebra in Mathematics: Solved Previous Year Questions

Question 1:

If $\vec{a}=\alpha \hat{i}+\beta \hat{j}+3 \hat{k}, \vec{b}=-\beta \hat{i}-\alpha \hat{j}-\hat{k}$ and $\vec{c}=\hat{i}-2 \hat{j}-\hat{k}$ such that $\vec{a} \cdot \vec{b}=1$ and $\vec{b} . \vec{c}=-3$, then $\frac{1}{3}((\vec{a} \times \vec{b}) \cdot \vec{c})$ is equal to:

Solution:

$
\begin{aligned}
& \vec{a}=\alpha \hat{i}+\beta \hat{j}+3 \hat{k}, \\
& \vec{b}=-\beta \hat{i}-\alpha \hat{j}-\hat{k} \text { and } \\
& \vec{c}=\hat{i}-2 \hat{j}-\hat{k} \\
& \vec{a} \cdot \vec{b}=1 \\
& \Rightarrow \quad-\alpha \beta-\alpha \beta-3=1 \\
& \Rightarrow \quad-2 \alpha \beta=4 \Rightarrow \alpha \beta=-2 \\
& \vec{b} \cdot \vec{c}=-3 \\
& \Rightarrow-\beta+2 \alpha+1=-3 \\
& \beta-2 \alpha=4 \quad \ldots(2)
\end{aligned}
$
Solving (1) & (2)

$
\begin{aligned}
(\alpha, \beta) & =(-1,2) \\
\frac{1}{3}[\vec{a} \vec{b} \vec{c}] & =\frac{1}{3}\left|\begin{array}{ccc}
\alpha & \beta & 3 \\
-\beta & -\alpha & -1 \\
1 & -2 & -1
\end{array}\right| \\
& =\frac{1}{3}\left|\begin{array}{ccc}
-1 & 2 & 3 \\
-2 & 1 & -1 \\
1 & -2 & -1
\end{array}\right| \\
& =\frac{1}{3}\left|\begin{array}{ccc}
0 & 0 & 2 \\
-2 & 1 & -1 \\
1 & -2 & -1
\end{array}\right| \\
& =\frac{1}{3}[2(4-1)]=2
\end{aligned}
$

Hence, the correct answer is 2.

Question 2:

Let $\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}$ and $\vec{b}=7 \hat{i}+\hat{j}-6 \hat{k}$.
If $\vec{r} \times \vec{a}=\vec{r} \times \vec{b}, \vec{r} \cdot(\hat{i}+2 \hat{j}+\hat{k})=-3$, then $\vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k})$ is equal to:

Solution:

$\begin{aligned} & \vec{r} \times \vec{a}-\vec{r} \times \vec{b}=0 \\ & \Rightarrow \vec{r} \times(\vec{a}-\vec{b})=0 \\ & \Rightarrow \vec{r}=\lambda(\vec{a}-\vec{b}) \\ & \Rightarrow \vec{r}=\lambda(-5 \hat{i}-4 \hat{j}+10 \hat{k}) \\ & \text { Also } \vec{r} \cdot(\hat{i}+2 \hat{j}+\hat{k})=-3 \\ & \Rightarrow \lambda(-5-8+10)=-3 \\ & \lambda=1 \\ & \text { Now } \vec{r}=-5 \hat{i}-4 \hat{j}+10 \hat{k} \\ & =\vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k}) \\ & =-10+12+10=12\end{aligned}$

Hence, the correct answer is 12.

Question 3:

Let $\vec{a}=\widehat{i}+2 \widehat{j}-3 \widehat{k}$ and $\vec{b}=2 \widehat{i}-3 \widehat{j}+5 \widehat{k}$. If $\vec{r} \times \vec{a}=\vec{b} \times \vec{r}$, $\vec{r} \cdot(\alpha \widehat{i}+2 \widehat{j}+\widehat{k})=3$ and $\vec{r} \cdot(2 \widehat{i}+5 \widehat{j}-\alpha \widehat{k})=-1, \alpha \epsilon R$, then the value of $\alpha+[\vec{r}]^2$ is equal to:

Solution:

$
\begin{aligned}
& \vec{r} \times \vec{a}=\vec{b} \times \vec{r} \Rightarrow \vec{r} \times(\vec{a}+\vec{b})=0 \\
& \vec{r}=\vec{\lambda}(\vec{a}+\vec{b}) \Rightarrow \vec{r}=\vec{\lambda}(\hat{i}+2 \hat{j}-3 \hat{k}+2 \hat{i}-3 \hat{j}+5 \hat{k}) \\
& \vec{r}=\vec{\lambda}(3 \hat{i}-\hat{j}+2 \hat{k}) \quad \ldots(1) \\
& \vec{r} \cdot(\alpha \hat{i}+2 \hat{j}+\hat{k})=3 \quad \ldots(\text { Given }) \\
& \vec{\lambda}(3 \hat{i}-\hat{j}+2 \hat{k}) \cdot(\alpha \hat{i}+2 \hat{j}+\hat{k})=3 \\
& \Rightarrow \quad \alpha \lambda=1 \\
& \vec{r} \cdot(2 \hat{i}+5 \hat{j}-\alpha \hat{k})=-1 \quad \ldots(\text { Given }) \\
& \vec{\lambda}(3 \hat{i}-\hat{j}+2 \hat{k}) \cdot(2 \hat{i}+5 \hat{j}-\alpha \hat{k})=-1 \\
& \Rightarrow \quad 2 \lambda \alpha-\lambda=1
\end{aligned}
$
Solve (2) $\&(3)$

$
\begin{aligned}
& \alpha=1, \lambda=1 \\
& \Rightarrow \quad \vec{r}=3 \hat{i}-\hat{j}+2 \hat{k} \\
& |\vec{r}|^2=14 \quad \& \quad \alpha=1 \\
& \alpha+|\vec{r}|^2=15
\end{aligned}
$

Hence, the correct answer is 15.

Question 4:

If $\vec{b} \times \vec{d}=0, \vec{a}=\vec{b}+\vec{c}, \vec{c} \cdot \vec{d}=0$ then $\frac{\vec{d} \times(\vec{a} \times \vec{d})}{|\vec{d}|^2}$ equals:

Solution:

$
\begin{aligned}
& \frac{\vec{d} \times(\vec{a} \times \vec{d})}{|\vec{d}|^2}=\frac{(\vec{d} \cdot \vec{d}) \vec{a}-(\vec{d} \cdot \vec{a}) \vec{d}}{|\vec{d}|^2} \\
& =\frac{|\vec{d}|^2}{|\vec{d}|^2}-\frac{(\vec{d} \cdot \vec{a})}{|\vec{d}|^2} \vec{d}
\end{aligned}
$
Now $\vec{a}=\vec{b}+\vec{c}$

$
\begin{aligned}
& \Rightarrow \vec{a} \cdot \vec{d}=\vec{b} \cdot \vec{d}+\vec{c} \cdot \vec{d} \\
& \Rightarrow \quad \vec{a} \cdot \vec{d}=\vec{b} \cdot \vec{d} \quad(\text { As } \vec{c} \cdot \vec{d}=0)
\end{aligned}
$
$
\begin{aligned}
& \text { (i) } \Rightarrow \frac{\vec{d} \times(\vec{a} \times \vec{d})}{|\vec{d}|^2}=\vec{a}-\frac{\vec{b} \cdot \vec{d}}{|\vec{d}|^2} \vec{d} \\
& =\vec{a}-\frac{|\vec{b}||\vec{d}|}{|\vec{d}|^2} \vec{d} \quad\left(\begin{array}{c}
\text { As } \vec{b} \times \vec{d}=0 \\
\Rightarrow \vec{b} \text { and } \vec{d} \\
\text { are parallel }
\end{array}\right) \\
& =\vec{a}-\frac{|\vec{b}|}{|\vec{d}|} \cdot|\vec{d}| \hat{d} \\
& =\vec{a}-|\vec{b}| \hat{d} \\
& =\vec{a}-|\vec{b}| \hat{b} \quad(\text { as } \vec{b} \text { and } \vec{d} \text { are parallel) }
\end{aligned}
$

$
\begin{aligned}
& =\vec{a}-\vec{b} \\
& =\vec{c}(\mathrm{As} \vec{a}=\vec{b}+\vec{c})
\end{aligned}
$

Hence, the correct answer is $\vec{c}$.

Question 5:

If $\tilde{\mathrm{a}}=\mathrm{i}-\mathrm{j}-\mathrm{k}, \tilde{\mathrm{b}}=\mathrm{i}-\mathrm{j}+\mathrm{k}$ and $\tilde{\mathrm{c}}=\mathrm{i}+2 \mathrm{j}-\mathrm{k}$, then $\vec{a} \times(\vec{b} \times \vec{c})$ equals:

Solution:

$\begin{aligned} & \vec{a} \times(\vec{b} \times \vec{c}) \\ & =(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c} \\ & =(1-2+1) \vec{b}-(1+1-1) \vec{c} \\ & =-\vec{c} \\ & =-i-2 j+k\end{aligned}$

Hence, the correct answer is ($-i-2 j+k$).

How to prepare for Vector Algebra?

Vector Algebra is one of the basic topics. You can prepare this topic by understanding a few basic concepts

• Start with the basic concept of a vector, and understand all the terms used in vector algebra.

• Representation of a vector is an important part of this chapter. You need to read all the questions meditatively.

• Vector is all about the direction with magnitude, so make sure that the direction given in the question and the direction obtained in the answer match properly.

• Make sure that after studying a certain section/concept, you solve questions related to those concepts without looking at the solutions and practice MCQ from the above-mentioned books and solve all the previous year problems asked in JEE.

• Don’t let any doubt remain in your mind, and clear all the doubts with your teachers or with your friends.

List of Topics related to Vector Algebra according to NCERT/JEE Mains

This section outlines all the key vector algebra topics as per the NCERT and JEE Main syllabus, helping you focus on important chapters and concepts for Class 12.

Vector Algebra in Different Exams

The chapter Vector Algebra introduces vectors as mathematical quantities that have both magnitude and direction. It is an important part of Class 12 Mathematics and is widely tested in board and competitive examinations. Questions from this chapter evaluate a student’s understanding of vector operations, scalar and vector products, and their geometrical interpretations. Regular practice of NCERT exercises and application-based questions helps students develop strong problem-solving skills and score well in examinations.

Important Books and Resources for Vector Algebra

Here you will find recommended books, resources, and reference materials that cover vector algebra class 12 formulas, solutions, and practice problems for thorough preparation.

NCERT Resources for Vector Algebra

This section highlights official NCERT resources like textbooks, solved examples, and exercises that explain vector algebra concepts clearly for Class 12 students.

• NCERT Maths Notes for Class 12th Chapter 10 Vector Algebra

• NCERT Maths Solutions for Class 12th Chapter 10 Vector Algebra

• NCERT Maths Exemplar Solutions for Class 12th Chapter 10 Vector Algebra

NCERT Subjectwise Resources

Here, you get subject-specific NCERT resources, including worked-out problems, notes, and exemplar solutions for class 12, helping in detailed understanding and practice.

Practice Questions based on Vector Algebra

This part provides practice questions and sample problems based on vector algebra formulas and methods, enabling students to strengthen problem-solving skills and exam readiness.

Conclusion

The chapter Vector Algebra builds a strong foundation for understanding quantities that involve both magnitude and direction, and their applications in mathematics and physics. By mastering vector operations, scalar and vector products, and their geometric interpretations, students develop effective problem-solving and analytical skills. This chapter is an important scoring area in Class 12 Mathematics and is essential for success in board examinations as well as competitive exams like JEE and NEET. Regular practice of NCERT problems and clear understanding of formulas ensure confidence and accuracy while solving vector-based questions.