Empty Set
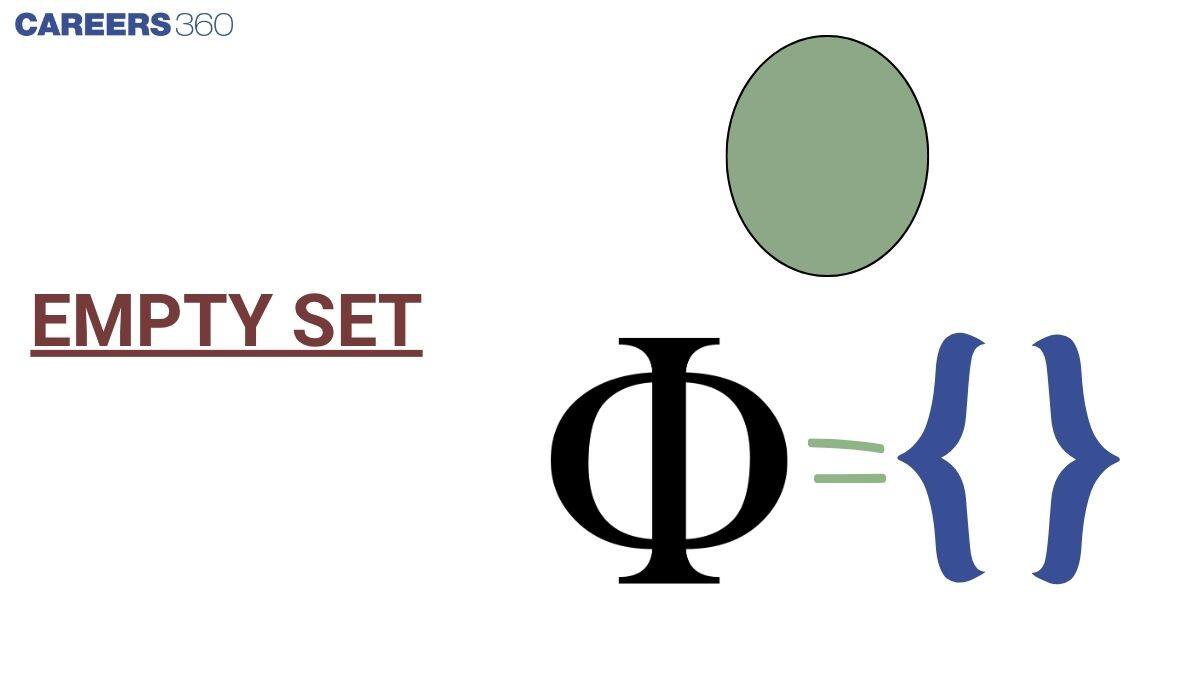
An empty set is a type of set that contains no elements at all. It is also called the null set and is denoted by the empty set symbol $\emptyset$ or $\{\}$. For example, the set of natural numbers less than $0$ is empty because no such number exists. In simple terms, an empty set is a set with zero elements. This article will help you understand what an empty set is, see examples of empty sets, learn its properties, and also find out whether the empty set is finite or infinite in mathematics. If you’re wondering which of the following sets is the empty set, keep reading to explore more with simple explanations and real-life examples.
This Story also Contains
- What is an Empty Set?
- Venn Diagram of Empty Set
- Properties of Empty Set
- Is the Empty Set Finite or Infinite?
- What is the difference between a Zero Set and an Empty Set?
- Empty Set Solved Examples
- Practice Questions
- NCERT Useful Resources
- List of related topics to Empty Set
What is an Empty Set?
An empty set is a set that contains no elements. It is also called the null set or void set. In other words, if a set has nothing inside it, it is considered an empty set.
The symbol for the empty set is either $\emptyset$ or $\{\}$. Is $Ø$ an empty set? Yes ,it is an empty set or null set.
Empty Set Notation
An empty set is usually written in one of the following ways:
- $\emptyset$
- $\{\}$
Both represent a set with zero elements.
Examples of Empty Set
Here are some common and easy-to-understand examples of empty sets:
- Set of natural numbers less than 0
$A = \{x \in \mathbb{N} \mid x < 0\}$
Since natural numbers start from 1, this set has no elements. So, $A = \emptyset$. - Set of real numbers whose square is negative
$B = \{x \in \mathbb{R} \mid x^2 + 1 = 0\}$
No real number satisfies this equation because $x^2$ is always non-negative. Hence, $B = \emptyset$. - Set of months with 32 days
$C = \{\text{months with 32 days}\}$
No month has 32 days, so this is also an empty set: $C = \emptyset$.
Note that: The cardinality (number of elements) of an empty set is 0, i.e.,
$n(\emptyset) = 0$
Venn Diagram of Empty Set
Venn diagrams are useful for showing relationships between sets. An empty set can be represented by leaving the region of the set blank, showing it contains no elements.
Consider a set $P =\{1, 0, 5\}$ and a set $Q = \{2, 8, 6\}$
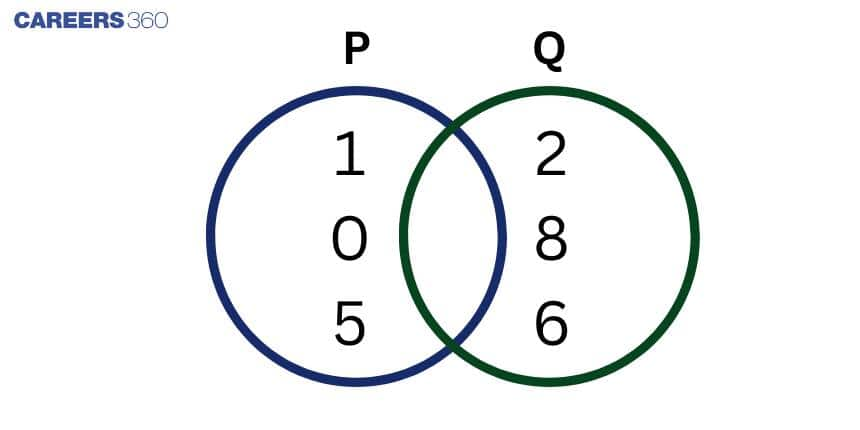
We can see that there are no common elements between the two sets P and Q, hence the intersection between these two sets is empty. So, P ∩ Q = ∅.
Properties of Empty Set
The empty set, also called the null set, plays a vital role in set theory. It has unique properties that help define operations and relationships between sets. Below are the most important properties of the empty set, explained with correct notation and symbols:
|
Property
|
Description
|
Mathematical Representation
|
|
Empty Set Symbol
|
The empty set is represented by the Greek letter phi or empty braces.
|
$\phi$ or $\{\}$
|
|
Cardinality
|
The number of elements in the empty set is zero.
|
0
|
|
Subset of Every Set
|
The empty set is a subset of every set.
|
$\phi \subseteq A,\ \forall A$
|
|
Subset of Empty Set
|
The only subset of an empty set is the empty set itself.
|
$A \subseteq \phi \Rightarrow A = \phi$
|
|
Cartesian Product
|
The Cartesian product of any set with the empty set is the empty set.
|
$A \times \phi = \phi,\ \forall A$
|
|
Power Set
|
The power set of the empty set contains only the empty set.
|
$2^{\phi} = {\phi}$
|
|
Union with Empty Set
|
Union with the empty set gives the set itself.
|
$A \cup \phi = A,\ \forall A$
|
|
Intersection with Empty Set
|
Intersection with the empty set gives the empty set.
|
$A \cap \phi = \phi,\ \forall A$
|
Remarks on Empty Set
- $\phi$ is called the null set.
- $\phi$ is unique, meaning there is only one empty set.
- $\phi$ is a subset of every set.
- $\phi$ is not written within braces; that is, ${\phi}$ is not the empty set.
- ${0}$ is not an empty set, as it contains the element $0$ (zero).
Example:
$\{x \mid x \in \mathbb{N},\ 4 < x < 5\} = \phi$
This set has no natural number between 4 and 5, so it is an empty set.
Is the Empty Set Finite or Infinite?
Is the Empty set countable? An empty set doesn't have any elements to count. However, the cardinality of an empty set is $0$. We can check the cardinality of a set by finding its cardinal number.
An empty set is a finite set because it has a defined and countable number of elements—specifically, zero. Its cardinality is $0$, which means the number of elements in the set is known.
In contrast, a set is called infinite if it has an uncountable or undefined number of elements, i.e., its cardinality is $\infty$. Since the empty set has no elements, and $0$ is a definite number, it is always finite.
What is the difference between a Zero Set and an Empty Set?
Though they may sound similar, the zero set and the empty set are different. This section explains how they differ based on elements, notation, and meaning in set theory.
|
Aspect
|
Empty Set
|
Zero Set
|
|
Definition
|
A set with no elements.
|
A set that contains only the number zero.
|
|
Notation
|
$\emptyset$ or $\{\}$
|
${0}$
|
|
Cardinality
|
$0$ (no elements)
|
$1$ (one element)
|
|
Contains 0?
|
Does not contain $0$ or any other element.
|
Contains only the element $0$.
|
|
Type of Set
|
Null/empty set
|
Singleton set
|
|
Example
|
$\{x \in \mathbb{N} \mid x < 0\}$
|
$\{x \in \mathbb{R} \mid x = 0\}$
|
Empty Set Solved Examples
Example 1: Which of the following is NOT true?
1) Equivalent sets can be equal.
2) Equal sets are equivalent.
3) Equivalent sets are equal.
4) None of these
Solution: In this Question,
Equivalent sets may or may not be equal sets, but equal sets always have the same number of elements, and hence equal sets are always equivalent.
Hence, the answer is option 3.
Example 2: Which of the following sets is the empty set?
1) $A=\{x: x$ is an even prime number $\}$
2) $B=\{x: x$ is an even number divisible by $3\}$
3) $C=\{x: x$ is an odd integer divisible by $6\}$
4) $D=\{x: x$ is an odd prime number $\}$
Solution: In this Question,
Option $1=\{2\}$, Option $2=\{6,12,18, \ldots$.$\}$ , Option $4=\{3,5,7, \ldots\}$
For option 3 , as there are no odd numbers divisible by $6$, so it is an empty set. Hence, the answer is option 3.
Example 3: Which of the following is not an empty set?
1) Real roots of $x^2+2 x+3=0$
2) imaginary roots of $x^2+3 x+2=0$
3) Real roots of $x^2+x+1=0$
4) Real roots of $x^4-1=0$
Solution:
Option (1) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (2) has real roots as Discriminant $>0$. So, there is no imaginary root, and the set is empty.
Option (3) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (4): $x^4-1=0 \Rightarrow\left(x^2-1\right)\left(x^2+1\right)=0$, which gives $x= \pm 1$.
Hence, it has $2$ real roots. So, it is not empty.
Hence, the answer is option 4.
Example 4: Which of the following is an empty set?
1) $\left\{x\right.$ : $x$ is a real number and $\left.x^2-1=0\right\}$
2) $\left\{x: x\right.$ is a real number and $\left.x^2+1=0\right\}$
3) $\left\{x\right.$ : $x$ is a real number and $\left.x^2-9=0\right\}$
4) $\left\{x\right.$ : $x$ is a real number and $\left.x^2+2=0\right\}$
Solution: Empty Set- A set which does not contain any element is called the empty set or the null set, or the void set.
Wherein e.g. $\{1<x<2, x$ is a natural number $\}$
Since $x^2+1=0$, gives $x^2=-1$
$\Rightarrow x= \pm i$
$\therefore$ $x$ is not a real but $x$ is real(given)
$\therefore$ value of $x$ is possible.
Example 5: If $A$ is universal set, then $((A′)′)′ $ is empty set. (True/False)
Solution: Given that A isthe universal set.
$(A')'= A$
$((A')')' = A'$
$A' = A - A = \phi$
So, the statement is true.
Practice Questions
Test your understanding of set concepts with these quick and concept-based MCQs. These questions are designed to help you identify and apply key ideas like equal and equivalent set definition, notation, subsets, finite and infinite sets, along with other topics, through simple and effective practice.
NCERT Useful Resources
Explore curated NCERT resources including notes, solutions, and exemplar problems covering all key set theory concepts like union of sets, intersection of sets, power set, singleton set, subsets, and more. These materials help in understanding and support effective exam preparation.
NCERT Maths Class 11 Chapter 1 Sets Solutions
List of related topics to Empty Set
To build a strong understanding of the Empty Set, it's helpful to explore other key set theory concepts that often relate to it. Topics such as Equal and Equivalent Sets, Subsets, Finite and Infinite Sets, Singleton Set, Power Set, and Universal Set provide essential context and connections. Learning these concepts together will enhance your ability to classify and analyse sets with precision.
Frequently Asked Questions (FAQs)
Empty set doesn't have any element to count. However, the cardinality of an empty set is $0$.
$\{0\}$ is not an empty set as it contains the element $0$ (zero).
Yes it is empty set or null set.
The other name of the empty set is the null set.