Equal and Equivalent Sets
Equal and equivalent sets are one of the most common types of sets in mathematics. In basic set theory, there are possibilities that two sets can be either equivalent, equal or unequal to one other. Now, let's look in detail about what is equal and equivalent sets.
Here, we will cover the concept of equal and equivalent sets. This concept falls under the broader category of sets, relation and function, a crucial chapter in class 11 mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.
JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days
JEE Main 2025: Maths Formulas | Study Materials
JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics
- Set
- Equal and Equivalent sets definition
- Properties of Equal and Equivalent Sets
- Difference Between Equal and Equivalent Sets
- Equal and Equivalent Sets Examples
Set
Sets can be defined as a collection of distinct objects, considered as a whole. These objects, also known as elements or members of the set, can be anything. For example, it can be from numbers, people, etc. They are particularly useful in defining and working with groups of objects that share common properties.
It is always a well-defined collection of distinct objects and is usually denoted by capital letters A, B, $\mathrm{C}, \mathrm{S}, \mathrm{U}, \mathrm{V} \ldots \ldots$. They can be written in any order but we must take care that elements are not repeated. They are generally denoted by a capital letter and curly braces '{}'.
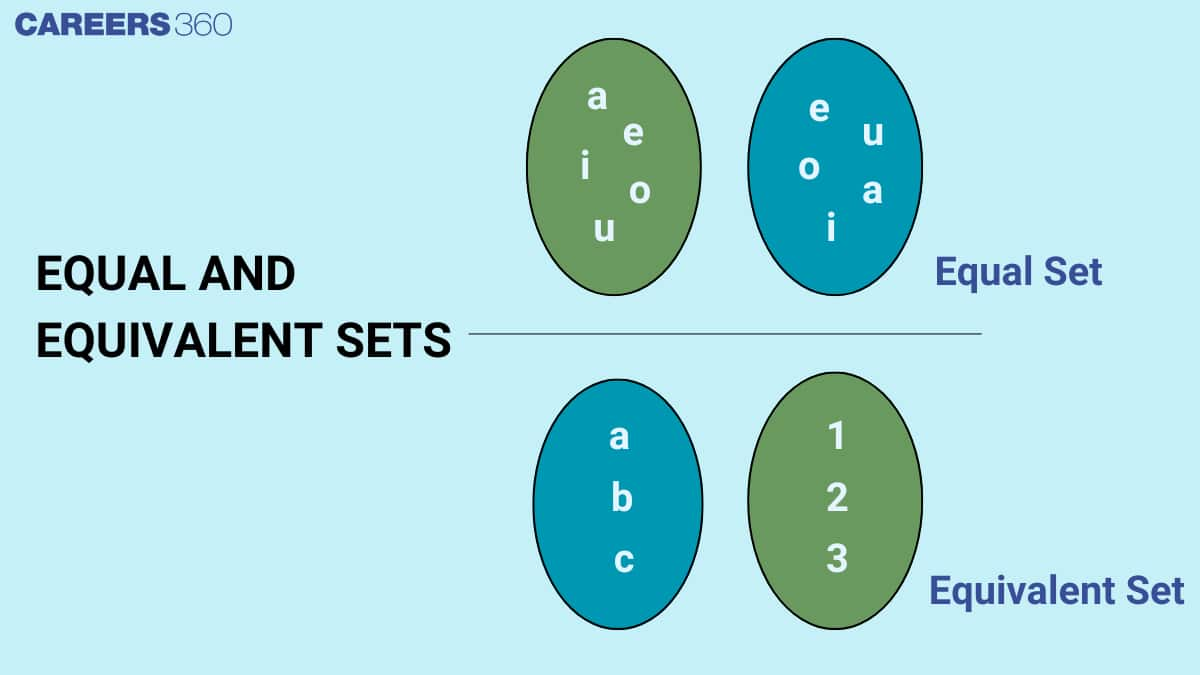
Equal and Equivalent sets definition
Now let us look in detail about the definition of equal and equivalent sets.
Equal Sets Definition
Equal sets are defined to be those sets that contain the same elements just as the other set with which we are comparing it and they suggest that there is a unique one-to-one relation in which each member of one of the sets is also a member of the other provided with the condition that they are without duplication or omission of any element.
Two sets $A$ and $B$ are said to be equal only if they have exactly the same elements and we write $A=$ B.
Otherwise, we conclude that the sets are unequal and hence we write $\mathrm{A} \neq \mathrm{B}$.
Example If $A=\{3,2,1,4\}$ and $B=\{2,3,4,1\}$, then both have exactly the same elements, and hence $\mathrm{A}=\mathrm{B}$.
Equal Sets Representation Using Venn Diagram
The Venn diagram below shows two equal sets P and Q with the same number of elements and equal elements, that is, P = {10, 17, 30} = Q.

Equivalent Sets Definition
We can define equivalent sets as those having the same number of elements, provided with the condition that there should be one to one relation between the elements of the two sets.
Form 1: If two sets $A$ and $B$ have the same cardinality if there exists an objective function from set $A$ to $B$.
Form 2: Two sets $A$ and $B$ are equivalent if they have the same cardinality that is $n(A)=n(B)$.
Example: $A=\{H, T, P, V\}$ and $B=\{1,2,3,4\}$, they both are equivalent as several elements in both are the same.
Equivalent Sets Representation Using Venn Diagram
The Venn diagram below shows two equivalent sets P and Q with the same number of elements, that is, P = {3, 6, 9} and Q = {a, b, c}.
Properties of Equal and Equivalent Sets
The properties of equal and equivalent sets are
Equal sets
1. Order of the elements does not affect their equality.
2. Equal sets are those sets that contain the same number of elements.
3. All the set elements are always equal in an equal set.
4. The cardinality as defined above is always equal for them.
5. The two sets are considered to be equal only when they are subsets of each other, denoted by $A \subseteq B$ and $B \subseteq A$,
6. All equal sets are also equivalent, but reverse is never true.
Equivalent Sets
1. If the number of elements in two or more sets is the same, then they are equal.
2. The cardinality of such sets is always the same.
3. We represent similar sets with the help of ~ or ≡.
4. Equivalent sets may or maynot be equal but reverse is always true.
Difference Between Equal and Equivalent Sets
Equal sets | Equivalent sets |
| If all elements are equal in two or more sets, then they are equal. | If the number of elements is the same in two or more sets, then are equivalent. |
| Equal sets have the same cardinality | Equivalent sets have the same cardinality. |
| They have the same number of elements. | They have the same number of elements. |
| The symbol used to denote equal sets is '=' | The symbol used to denote equivalent sets is ~ or ≡ |
| All equal sets are equivalent sets. | Equivalent sets may or may not be equal. |
| Elements should be the same. | Elements need not be the same. |
Equal and Equivalent Sets Examples
Example 1: Which of the following are equal sets?
1) $A=\{1,2,3,4\}$ and $B=$ collection of natural numbers less than 6
2) $A=\{$ prime numbers less than 6$\}$ and $B=\{$ prime factors of 30$\}$
3) $A=\{0\}$ and $B=\{x: x>15$ and $x<5\}$
Solution
In option (1), $A=\{1,2,3,4\}$ but $B=\{1,2,3,4,5\}$, hence not equal.
In option (2), $A=\{2,3,5\}$ but $B=\{2,3,5\}$, hence equal.
In option (3), $A=\{0\}$ but $B=$ Null set, hence not equal.
Hence, the answer is the option (2).
Example 2: Which of the following is NOT true?
1) Equivalent sets can be equal.
2) Equal sets are equivalent.
3) Equivalent sets are equal.
4) None of these
Solution
As we learned
In this Question,
Equivalent sets may or may not be equal sets but equal sets always have the same number of elements and hence equal sets are always equivalent.
Hence, the answer is the option 3.
Example 3: Which of the following are equal sets?
1) $A_1$ is a set of letters of ALLOY and $B_1$ is a set of letters of LOYAL.
2) $A_2=\left\{n: n \in Z\right.$ and $\left.n^2 \leq 4\right\}$ and $B_2=\left\{n: n^2-3 n+2=0\right\}$
3) $A_3=\left\{x: x^2=9\right\}$ and $B_3=\{3\}$
4) $A_4=\{x: x$ is a vowel $\}$ and $B_4=\{\mathrm{a}, \mathrm{e}, \mathrm{i}, \mathrm{u}\}$
Solution
(1) $A_1=\{\mathrm{A}, \mathrm{L}, \mathrm{O}, \mathrm{Y}\}$, and $B_1=\{\mathrm{L}, \mathrm{O}, \mathrm{Y}, \mathrm{A}\}$, these are equal sets since they have exactly the same elements.
(2) $A_2=\{-2,-1,0,1,2\}, B_2=\{1,2\}$, so unequal.
(3) $A_3=\{3,-3\}, B_3=\{3\}$, so unequal.
(4) $A_4=\{a, e, i, o, u\}, B_4=\{a, e, i, u\}$, so unequal.
Hence, the answer is the option (1).
Example 4: Which of the following is not an empty set?
1) Real roots of $x^2+2 x+3=0$
2) imaginary roots of $x^2+3 x+2=0$
3) Real roots of $x^2+x+1=0$
4) Real roots of $x^4-1=0$
Solution
Option (1) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (2) has real roots as Discriminant $>0$. So, there is no imaginary root, and the set is empty.
Option (3) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (4): $x^4-1=0 \Rightarrow\left(x^2-1\right)\left(x^2+1\right)=0$, which gives $x= \pm 1$
Hence, it has 2 real roots. So, it is not empty.
Hence, the answer is the option 4.
Example 5: Which of the following are NOT equivalent sets?
1) $P=\{A, B, C, D, E\}$ and $Q=\{$ Jan,Feb,Mar,April,May $\}$
2) $P=\{x: x$ is a prime number on dice $\}$ and $Q=\{x: x$ is an even number on dice $\}$
3) $P=\left\{x: x \in R\right.$ and $\left.x^2-5 x+6=0\right\}$ and $Q=\left\{x: x \in R\right.$ and $\left.x^2-4 x+5=0\right\}$
4) $A=\{x: x$ is a vowel $\}$ and $B=\{x: x$ is a natural number less than 6$\}$
Solution
In (A), both sets have $5$ elements, hence they are equivalent.
In (B), $P=\{2,3,5\}$ and $Q=\{2,4,6\}$, hence equivalent.
In (C), $P$ has 2 elements as there are 2 roots of $x^2-5 x+6=0$ (as discriminant $>0$ ) but $x^2-4 x+5=0$ has no real roots (as discriminant $<0$ ), so $Q$ is empty, hence they are not equivalent.
In (D), both sets have $5$ elements, hence they are equivalent.
Hence, the answer is the option 3.
List of Topics Related to Equal and Equivalent Sets
Frequently Asked Questions (FAQs)
Equal sets can be defined as those sets that contain the same or equal elements as the other and they suggest that there is a one-to-one relationship in which each member of one of the sets is also a member of the other without duplication or omission of any element. Two sets having the same number of elements are called equivalent sets.
Example of equal and equivalent sets are as follows-
Equal set: Let $A$ be set of natural numbers and $B$ be set of whole numbers greater than $0$. $A = \{1,2,3,4,5,6....\}$ and $B = \{1,2,3,4,5,6,....\}$ have the same exact elements. So, the sets $A$ and $B$ are equal sets.
Equivalent set: Let $A$ be natural numbers less than $6$ and $B$ be whole numbers less than $5$. The cardinality of both sets $A$ and $B$ are equal. So, the sets $A$ and $B$ are equal.
Comparable set means that each element of one set can be paired with exactly one element of other set, and vice versa.
The difference between equal and equivalent sets can be stated as - sets are equal if all elements are equal in two or more sets whereas if the number of elements in two or more sets is the same, they are equivalent sets.
When comparing, two sets, one has to check whether ' $A$ ' and ' $B$ ' are composed of the same elements or not. For example, set $A$ was defined as the set of $\{2,3,4\}$ and set $B$ was also defined as the set of $\{4,3,2\}$ and thus set $A$ and set $B$ are equal sets. Comparing two sets requires us to consider how many elements each set contains to come up with the conclusion that the two are equivalent.
Also Read
20 Jan'25 04:44 PM
20 Jan'25 04:42 PM
20 Jan'25 04:40 PM
20 Jan'25 04:39 PM
18 Dec'24 01:59 AM
18 Dec'24 01:57 AM
18 Dec'24 01:55 AM
18 Dec'24 01:49 AM
18 Dec'24 01:11 AM
18 Dec'24 12:58 AM