Tangent to a Curve

Edited By Komal Miglani | Updated on Jul 02, 2025 07:56 PM IST

Tangent to the curve at a point is an important concept in calculus. It is useful in understanding the relationship between curves and their slopes. The tangent line to the curve is a straight line that touches a curve at a single point without crossing it at that point. These concepts of Tangents and slopes have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

This Story also Contains

Tangent to the Curve at point:
Slope and Equation of Tangent
Equation of Tangent
Tangent from External Point
Solved Examples Based on Equation of Tangent to the Curve

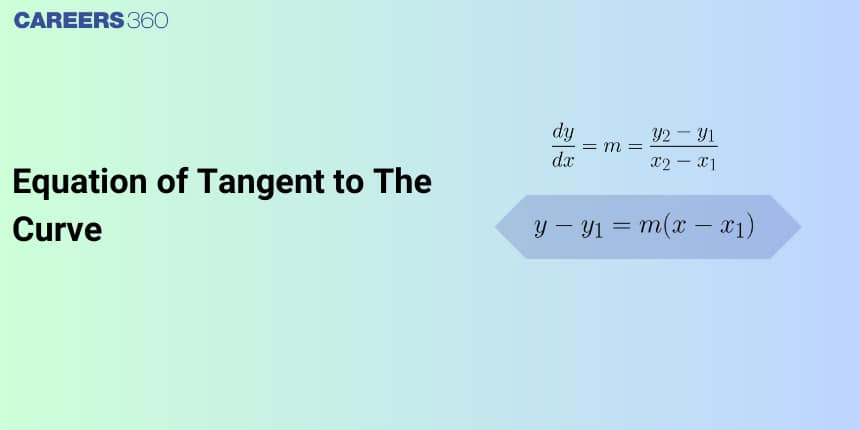
Tangent to a Curve

In this article, we will cover the concept of the Tangent to the Curve at a Point. This topic falls under the broader category of Calculus, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of nineteen questions have been asked on this topic in JEE Main from 2013 to 2023, including two questions in 2013, one question in 2016, one question in 2017, five questions in 2020, two in 2021, seven in 2022 and one in 2023.

Tangent to the Curve at point:

The tangent to a curve at a point P on it is defined as the limiting position of the secant $P Q$ as the point $Q$ approaches the point $P$ provided such a limiting position exists.

The slope of the tangent to the curve $y=f(x)$ at the point $\left(x_0, y_0\right)$ is given by $\left.\frac{d y}{d x}\right]_{\left(x_0, y_0\right)} \quad\left(=f\left(x_0\right)\right)$. So the equation of the tangent at $\left(x_0, y_0\right)$ to the curve $y=f(x)$ is given by $y-y_0=f^{\prime}\left(x_0\right)\left(x-x_0\right)$.

Normal

The normal to the curve at any point P on it is the straight line which passes through $P$ and is perpendicular to the tangent to the curve at $P$

Slope and Equation of Tangent

Let $P\left(x_0, y_0\right)$ be a point on the continuous curve $y=f(x)$, then the slope of the tangent to the curve at point $P$ is

$
\begin{aligned}
& \left(\frac{d y}{d x}\right)_{\left(x_0, y_0\right)} \\
& \Rightarrow\left(\frac{d y}{d x}\right)_{\left(x_0, y_0\right)}=\tan \theta=\text { slope of tangent at } P
\end{aligned}
$
Where $\theta$ is the angle which the tangent at $\mathrm{P}\left(\mathrm{x}_0, \mathrm{y}_0\right)$ makes with the positive direction of the $x$-axis as shown in the figure.

If the tangent is parallel to $x$-axis then $\theta=0^{\circ}$.
$
\begin{aligned}
& \Rightarrow \quad \tan \theta=0 \\
& \therefore \quad\left(\frac{d y}{d x}\right)_{\left(x_0, y_0\right)}=0
\end{aligned}
$
If the tangent is perpendicular to $x$-axis then $\Theta=90^{\circ}$
$
\begin{aligned}
& \Rightarrow \quad \tan \theta \rightarrow \infty \quad \text { or } \quad \cot \theta=0 \\
& \therefore\left(\frac{d x}{d y}\right)_{\left(x_0, y_0\right)}=0
\end{aligned}
$

Equation of Tangent

Let the equation of curve be $y=f(x)$ and let point $P\left(x_0, y_0\right)$ lies on this curve.

The slope of the tangent to the curve at a point $P$ is

$
\left(\frac{d y}{d x}\right)_{\left(x_0, y_0\right)}
$
Hence, the equation of the tangent at point $P$ is

$
\left(y-y_0\right)=\left(\frac{d y}{d x}\right)_{\left(x 0, y_0\right)} \cdot\left(x-x_0\right)
$

Tangent from External Point

If a point $Q(a, b)$ does not lie on the curve $y=f(x)$, then the equation of possible tangent to the curve $y=f(x)$ (tangent passing through point $Q$ ( $a$, b)) can be found by first getting the point of contact $\mathrm{P}\left(\mathrm{x}_0, \mathrm{y}_0\right)$ on the curve.

$P\left(x_0, y_0\right)$ lies on the curve $\mathrm{y}=\mathrm{f}(\mathrm{x})$, then

$
y_0=f\left(x_0\right)
$
Also, slope of PQ is

$
\frac{y_0-b}{x_0-a}=\left(\frac{d y}{d x}\right)_{\left(x_0, y_0\right)}
$
By solving the above two equations we get the point of contact point $P$.
Using P we can find the equation of tangent PQ .

Solved Examples Based on Equation of Tangent to the Curve

Example 1: Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be a point on the curve $y=x^2+7 x+2$, nearest to the line, $y=3 x-3$, Then the equation of the normal to the curve at $P$ is:
1) $x+3 y+26=0$
2) $x+3 y-26=0$
3) $x-3 y-11=0$
4) $x-3 y+22=0$

Solution

Let $L$ be the common normal to the parabola $y=x^2+7 x+2$ and line $y=3 x-3$
$\Rightarrow$ slope of tangent of $y=x^2+7 x+2$ at $P=3$ $\left.\Rightarrow \frac{\mathrm{dy}}{\mathrm{dx}}\right]_{\text {for } \mathrm{P}}=3$

$
\Rightarrow 2 x+7=3 \Rightarrow x=-2 \Rightarrow y=-8
$
So $\mathrm{P}(-2,-8)$
Normal at $\mathrm{P}: \mathrm{x}+3 \mathrm{y}+\mathrm{C}=0$
$\Rightarrow C=26$ ( $P$ satifies the line)
Normal : $x+3 y+26=0$

Example 2: The shortest distance between the line $x-y=1$ and the curve $x^2=2 y$ is:
1) $\frac{1}{2}$
2) $\frac{1}{2 \sqrt{2}}$
3) $\frac{1}{\sqrt{2}}$
4) 0

Solution

The shortest distance between curves is always along the common normal.

the slope of the line

$\frac{d y}{d x}=1=$ slope of the line
$P$ is any point on the parabola, and also tangent pass through point $P$
slope of the tangent to the parabola

$
\begin{aligned}
& 2 x=2 \frac{d y}{d x} \\
& \frac{d y}{d x}=x=1 \\
& \Rightarrow y=\frac{1}{2}
\end{aligned}
$
Point $\mathrm{P}=\left(1, \frac{1}{2}\right)$
$\therefore$ Shortest distance $=\left|\frac{1-\frac{1}{2}-1}{\sqrt{1^2+1^2}}\right|=\frac{1}{2 \sqrt{2}}$

Example 3 : If the tangent to the curve $y=x^3-x^2+x$ at the point $(\mathrm{a}, \mathrm{b})$ is also tangent to the curve $\mathrm{y}=5 \mathrm{x}^2+2 \mathrm{x}-25$ at the point $(2,-1)$, then $|2 \mathrm{a}+9 \mathrm{~b}|$ is equal to $\qquad$
1) 195
2) 48
3) 23
4) 50

Solution

Equation of tangent to $y=5 x^2+2 x-25$ at $(2,-1)$

$
\begin{aligned}
& y^{\prime}=10 x+2=20+2=22 \\
& y+1=22(x-2) \\
& y+1=22 x-44 \\
& y=22 x-45
\end{aligned}
$
This is also tangent to $\mathrm{y}=\mathrm{x}^3-\mathrm{x}^2+\mathrm{x}$ at $(\mathrm{a}, \mathrm{b})$

Finding point of intersection

$
\begin{aligned}
& 22 \mathrm{x}-45=\mathrm{x}^3-\mathrm{x}^2+\mathrm{x} \\
\Rightarrow & \mathrm{x}^3-\mathrm{x}^2-21 \mathrm{x}+45=0 \\
\Rightarrow & (\mathrm{x}-3)^2(\mathrm{x}+5)=0
\end{aligned}
$
Tangent at $\mathrm{x}=3 \Rightarrow \mathrm{a}=3$
Put $\mathrm{x}=3$ in $\mathrm{y}=22 \mathrm{x}-45$

$
\begin{aligned}
& \Rightarrow \mathrm{b}=66-45=21 \\
& \therefore|2 \mathrm{a}+9 \mathrm{~b}|=6+189=195
\end{aligned}
$
Ans:195

Example 4: Let $\mathrm{P}(\mathrm{a}, \mathrm{b})$ be a point on the parabola $\mathrm{y}^2=8 \mathrm{x}$ such that the tangent at P passes through the centre of the circle $x^2+y^2-10 x-14 y+65=0$. Let A be the product of all possible values of $a$ and $B$ be the product of all possible values of $b$. Then the value of $\mathrm{A}+\mathrm{B}$ is equal to
1) 0
2) 25
3) 40
4) 65

Solution

$\mathrm{P}(\mathrm{a}, \mathrm{b})$ is point on $\mathrm{y}^2=8 \mathrm{x}$, such that tangent at P pass through centre of

$
x^2+y^2-10 x-14 y+65=0 \quad \text { i.e }(5,7)
$
Tangent at $\mathrm{P}\left(\mathrm{at}^2, 2 \mathrm{at}\right)$ is ty $=\mathrm{x}+\mathrm{at}^2$
$\mathrm{A}=2 \&$ it pass through $(5,7)$
$7 \mathrm{t}=5+2 \mathrm{t}^2$
$\Rightarrow \mathrm{t}=1, \mathrm{t}=\frac{5}{2}$
$\therefore \mathrm{P}\left(\mathrm{at}^2, 2 \mathrm{at}\right) \Rightarrow(2,4)$ when $\mathrm{t}=1$
$\&\left(\frac{25}{2}, 10\right)$ when $t=\frac{5}{2}$
$\therefore \mathrm{A}=2 \times \frac{25}{2}=25$
$\therefore A+B=65$
Hence, the answer is the option(4).

Example 5: Let M and N be the number of points on the curve $\mathrm{y}^5-9 \mathrm{xy}+2 \mathrm{x}=0$, where the tangents to the curve are parallel to x axis and $y$-axis, respectively. Then the value of $\mathrm{M}+\mathrm{N}$ equals $\qquad$
1) 2
2) 3
3) 4
4) 5

Solution
$
\begin{aligned}
& y^5-9 x y+2 x=0 \\
& 5 y^4 \frac{d y}{d x}-9 x \frac{d y}{d x}-9 y+2=0 \\
& \frac{d y}{d x}\left(5 y^4-9 x\right)=9 y-2 \\
& \frac{d y}{d x}=\frac{9 y-2}{5 y^4-9 x}=0 \text { (for horizontal tangent) } \\
& y=\frac{2}{9} \Rightarrow \text { which does rot satisfy the original equation } \Rightarrow m=0
\end{aligned}
$
Now $5 \mathrm{y}^4-9 \mathrm{x}=0$ (for vertical tangent )

$
\begin{aligned}
& 5 y^4(9 y-2)-9 y^5=0 \\
& y^4[45 y-10-9 y]=0 \\
& y=0 \text { or } 36 y=10 \\
& y=\frac{5}{18} \\
& y=0 \Rightarrow x=0 \& y=\frac{5}{18} \Rightarrow x(0,0)\left(x, \frac{5}{18}\right) \\
& N=2 \\
& M+N=0+2=2
\end{aligned}
$

Hence, the answer is the option(1).

Frequently Asked Questions (FAQs)

1. What is a tangent to a curve?

A tangent to a curve is a straight line that touches the curve at a single point without crossing it. At the point of contact, the tangent line has the same slope as the curve, representing the instantaneous rate of change of the function at that point.

2. How is the slope of a tangent line related to the derivative of a function?

The slope of the tangent line at a point on a curve is equal to the derivative of the function at that point. This relationship is fundamental in calculus and allows us to find the equation of the tangent line using the function's derivative.

3. Can a curve have more than one tangent line at a single point?

Generally, a smooth curve has only one tangent line at a given point. However, at cusps or corners where the curve is not differentiable, there may be multiple tangent lines or no tangent line at all.

4. What's the difference between a secant line and a tangent line?

A secant line intersects a curve at two or more points, while a tangent line touches the curve at only one point. As the two points of a secant line get closer together, the secant line approaches the tangent line at that point.

5. How do you find the equation of a tangent line to a curve?

To find the equation of a tangent line: 1) Find the derivative of the function. 2) Evaluate the derivative at the point of tangency to get the slope. 3) Use the point-slope form of a line (y - y1 = m(x - x1)) with the point of tangency and the calculated slope.

6. What does it mean if a function is not differentiable at a point?

If a function is not differentiable at a point, it means that the function doesn't have a well-defined tangent line at that point. This can occur at sharp corners, cusps, or discontinuities in the function.

7. How is the concept of tangent lines used in optimization problems?

In optimization problems, tangent lines help find maximum or minimum values of functions. At these extreme points, the tangent line is often horizontal (slope = 0), which corresponds to the derivative being zero at those points.

8. Can a tangent line ever cross the curve it's tangent to?

While a tangent line touches the curve at a single point locally, it may intersect the curve at other points. This is common with more complex curves. The key is that near the point of tangency, the line only touches the curve at that one point.

9. What's the relationship between tangent lines and the graph's concavity?

The position of the tangent line relative to the curve indicates the graph's concavity. If the curve lies above its tangents, it's concave up. If it lies below, it's concave down. This relates to the second derivative's sign.

10. How do you visualize the tangent line's slope approaching a point?

Imagine a secant line through two points on the curve. As one point moves closer to the other, the secant line rotates. The limiting position of this rotating secant line as the points get infinitely close is the tangent line.

11. What's the significance of the tangent line in linear approximation?

The tangent line provides a linear approximation of the function near the point of tangency. This is useful for estimating function values and is the basis for many numerical methods and Taylor series approximations.

12. How does the concept of tangent lines extend to three-dimensional surfaces?

For 3D surfaces, we use tangent planes instead of tangent lines. A tangent plane touches the surface at a single point and is determined by two tangent vectors at that point, representing the surface's slope in two independent directions.

13. What's the connection between tangent lines and the chain rule in calculus?

The chain rule relates the derivatives of composite functions. Geometrically, it describes how the slopes of tangent lines to different curves are related when one function is composed with another.

14. How do you find the angle between two curves using tangent lines?

To find the angle between two curves at their intersection point: 1) Find the slopes of the tangent lines to each curve at the intersection. 2) Use the formula: tan(θ) = |m1 - m2| / (1 + m1m2), where m1 and m2 are the slopes.

15. What does it mean for a function to be "smooth" in terms of tangent lines?

A smooth function has a well-defined tangent line at every point, meaning it's continuous and differentiable everywhere. The tangent line changes direction gradually as you move along the curve without any abrupt changes or breaks.

16. How are tangent lines related to the Mean Value Theorem?

The Mean Value Theorem states that for a continuous, differentiable function on a closed interval, there exists a point where the tangent line is parallel to the secant line connecting the interval's endpoints. This tangent line's slope equals the average rate of change over the interval.

17. Can a vertical line ever be a tangent line to a function graph?

A vertical line cannot be a tangent line to the graph of a function. Functions, by definition, can only have one y-value for each x-value. A vertical tangent would imply multiple y-values for a single x, violating the function definition.

18. How do you determine if a line is tangent to a circle?

A line is tangent to a circle if it touches the circle at exactly one point. Algebraically, this occurs when the distance between the line and the circle's center equals the circle's radius, or when the discriminant of the quadratic equation formed by their intersection is zero.

19. What's the relationship between a function's critical points and its tangent lines?

At a function's critical points, the tangent line is either horizontal (slope = 0) or undefined. These points are potential locations for local maxima, minima, or inflection points, and are crucial in analyzing the function's behavior.

20. How do tangent lines relate to the derivative's sign and a function's behavior?

The sign of the derivative (positive, negative, or zero) corresponds to the slope of the tangent line (increasing, decreasing, or horizontal). This relationship helps in sketching graphs and understanding a function's overall behavior.

21. What's the difference between a tangent and a normal line?

A tangent line touches the curve at a single point and is parallel to the curve at that point. A normal line is perpendicular to the tangent line at the point of contact, intersecting the curve at a right angle.

22. How do you find the points on a curve where the tangent line has a specific slope?

To find points where the tangent has a specific slope: 1) Set the derivative of the function equal to the desired slope. 2) Solve this equation for x. 3) Use these x-values in the original function to find the corresponding y-values.

23. What's the significance of the tangent line in Newton's Method?

Newton's Method uses tangent lines to approximate roots of functions. It starts with an initial guess and iteratively finds better approximations by following the tangent line at each point to its x-intercept, which becomes the next guess.

24. How do you determine if a curve has a horizontal tangent line?

A curve has a horizontal tangent line at points where its derivative equals zero. To find these points: 1) Take the derivative of the function. 2) Set it equal to zero. 3) Solve for x. These x-values give the locations of horizontal tangents.

25. What's the relationship between tangent lines and limits?

The slope of a tangent line at a point is defined as the limit of the slopes of secant lines as the second point approaches the point of tangency. This concept forms the foundation of differential calculus and the formal definition of derivatives.

26. How do tangent lines help in understanding continuity?

The existence of a tangent line at a point implies that the function is both continuous and differentiable at that point. Discontinuities or non-differentiable points (like cusps or corners) are places where tangent lines cannot be defined.

27. What's the connection between tangent lines and implicit differentiation?

Implicit differentiation allows us to find tangent lines to curves that are not functions or cannot be easily expressed as y = f(x). It involves differentiating both sides of an equation with respect to x, treating y as a function of x.

28. How do you find the equation of a line tangent to a parametric curve?

For a parametric curve (x(t), y(t)): 1) Find dx/dt and dy/dt. 2) Evaluate these at the desired t-value. 3) The slope of the tangent line is (dy/dt) / (dx/dt). 4) Use this slope and the point (x(t), y(t)) in the point-slope form of a line.

29. What's the significance of tangent lines in understanding function behavior near asymptotes?

Near vertical asymptotes, tangent lines become increasingly steep. Near horizontal asymptotes, tangent lines become increasingly horizontal. This helps visualize how the function approaches infinity or a specific value as x approaches certain values.

30. How do tangent lines relate to the concept of local linearity?

Tangent lines embody the principle of local linearity: that any smooth function can be approximated by a straight line over a small enough interval. This is the foundation for many calculus concepts and numerical approximation methods.

31. What's the relationship between tangent lines and the intermediate value theorem?

While not directly related, both concepts involve continuity. The intermediate value theorem guarantees that a continuous function takes on all values between any two of its function values. This continuity is necessary for the existence of tangent lines at all points.

32. How do you find points on a curve where the tangent line is parallel to a given line?

To find such points: 1) Set the derivative of the function equal to the slope of the given line. 2) Solve this equation for x. 3) Use these x-values in the original function to find the corresponding y-values. These (x,y) pairs are the desired points.

33. What's the geometric interpretation of the second derivative in terms of tangent lines?

The second derivative describes how the slope of the tangent line changes as you move along the curve. A positive second derivative means the slope is increasing (curve bending upward), while a negative second derivative means the slope is decreasing (curve bending downward).

34. How do tangent lines help in understanding the behavior of inverse functions?

The tangent line to a function and the tangent line to its inverse at corresponding points are perpendicular to each other. This relationship helps in visualizing and analyzing inverse functions, especially when graphing them.

35. What's the connection between tangent lines and the definition of e as the base of natural logarithms?

The number e is defined such that the tangent line to the curve y = e^x at x = 0 has a slope of 1. This unique property makes e the natural base for exponential and logarithmic functions in calculus.

36. How do you find the points on a curve where the tangent line passes through the origin?

To find such points: 1) Express the slope of the tangent line as f'(x). 2) The line through the origin has the equation y = mx, where m = f'(x). 3) Solve the equation f(x) = xf'(x) for x. These x-values give the desired points.

37. What's the significance of tangent lines in understanding function symmetry?

For even functions (symmetric about y-axis), tangent lines at opposite x-values have opposite slopes. For odd functions (symmetric about origin), tangent lines at opposite x-values have equal slopes. This helps in verifying and understanding function symmetry.

38. How do tangent lines relate to the concept of differentials in calculus?

Differentials represent small changes in variables. Geometrically, they correspond to small movements along the tangent line to a curve. The ratio of differentials (dy/dx) represents the slope of this tangent line, connecting to the derivative concept.

39. What's the relationship between tangent lines and the definition of convex and concave functions?

For a convex function, any tangent line lies entirely below the graph (except at the point of tangency). For a concave function, any tangent line lies entirely above the graph. This property is crucial in optimization and inequality problems.

40. How do you determine if a curve has a vertical tangent line?

A curve has a vertical tangent line at points where its derivative is undefined or approaches infinity. This often occurs at cusps or where the function's rate of change becomes extremely large in a vertical direction.

41. What's the connection between tangent lines and the fundamental theorem of calculus?

The fundamental theorem of calculus relates derivatives to integrals. Geometrically, it shows that the area under a curve (integral) can be found using antiderivatives, which are related to the slopes of tangent lines (derivatives) at each point.

42. How do tangent lines help in understanding the behavior of trigonometric functions?

Tangent lines to trigonometric functions help visualize their periodic nature and rate of change. For example, the tangent line to sin(x) at x = 0 has a slope of 1, which is key in small angle approximations and Taylor series expansions.

43. What's the significance of tangent lines in understanding function composition?

When composing functions, the chain rule shows how the slopes of tangent lines are related. The slope of the tangent to the composite function is the product of the slopes of the tangent lines to the individual functions at corresponding points.

44. How do you find the equation of a tangent line to a polar curve?

For a polar curve r = f(θ): 1) Convert to parametric form: x = r cos(θ), y = r sin(θ). 2) Find dx/dθ and dy/dθ. 3) The slope of the tangent line is (dy/dθ) / (dx/dθ). 4) Use this slope and the point (r cos(θ), r sin(θ)) in the point-slope form.

45. What's the relationship between tangent lines and the concept of one-sided limits?

One-sided limits relate to the behavior of a function as it approaches a point from either the left or right. This concept is crucial in understanding the existence and continuity of tangent lines, especially at points where the function behavior changes abruptly.

46. How do tangent lines help in understanding the behavior of piecewise functions?

Tangent lines can help identify if a piecewise function is continuous and/or differentiable at the points where the function definition changes. The existence and continuity of tangent lines at these points indicate the smoothness of the transition between pieces.

47. What's the significance of tangent lines in understanding function transformations?

When a function is transformed (shifted, stretched, or reflected), its tangent lines undergo corresponding transformations. This helps in visualizing how the function's rate of change is affected by various transformations.

48. How do tangent lines relate to the concept of linearization in multivariable calculus?

In multivariable calculus, linearization extends the idea of tangent lines to tangent planes or hyperplanes. These linear approximations of multivariable functions near a point are crucial for understanding local behavior and in optimization problems.

49. What's the connection between tangent lines and Taylor series expansions?

The first-order Taylor polynomial of a function at a point is precisely the equation of the tangent line at that point. Higher-order terms in the Taylor series provide increasingly accurate polynomial approximations of the function near the point of expansion.

50. How do tangent lines help in understanding the concept of function approximation?

Tangent lines provide the simplest form of local linear approximation for a function. This concept is fundamental in numerical methods, error analysis, and understanding how complex functions can be approximated by simpler ones over small intervals.