Escribed Circle of Triangle: Definition & Meaning

In geometry, the triangle plays a very important role. A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. So, finding the different properties of the triangle is essential. The area of a triangle is the region enclosed by the three sides of the triangle.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. Triangle
2. Escribed Circle of Triangle
3. Solved Examples Based on Escribed Circle of Triangle

Triangle

A triangle is a polygon with 3 sides. A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. A triangle has six main elements, three sides, and three angles. There are different rules and theorems for triangles that relate their sides and angles.

A few standard symbols to represent elements of the triangle:
In $\triangle A B C$, the angles are denoted by capital letters $A, B$, and $C$, and the length of the sides opposite to these angles are denoted by small letters $a, b$, and c respectively.

The following symbols in relation to ΔABC are universally adopted.

Angles: $\angle B A C=A, \angle A B C=B, \angle B C A=C$
Sides: $\mathrm{AB}=\mathrm{c}, \mathrm{AC}=\mathrm{b}$, and $\mathrm{BC}=\mathrm{a}$
Semi-perimeter of the $\triangle \mathrm{ABC}$, is $s=\frac{a+b+c}{2}$ and it is denoted by s . So, the perimeter of $\triangle \mathrm{ABC}$ is $2 \mathrm{~s}=\mathrm{a}+\mathrm{b}+\mathrm{c}$.

The area of a triangle is denoted by $S$ or $\Delta$.
For any $\triangle A B C$,
- $A+B+C=180^{\circ}$
- $a+b>c, b+c>a$ and $c+a>b$
- $a>0, b>0, c>0$

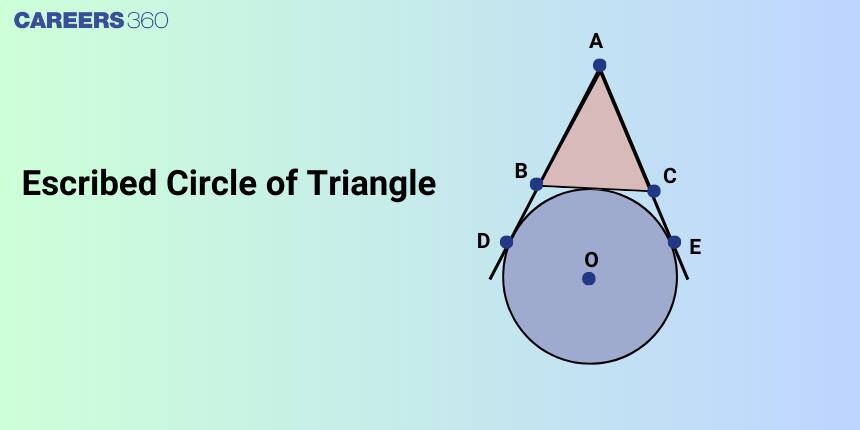
Escribed Circle of Triangle

The circle that touches the side $B C$ and two sides $A B$ and $A C$ produced of triangle $A B C$ is called the escribed circle opposite to the angle $A$. Its radius is denoted by $r_1$. Similarly, $r_2$ and $r_3$ denote the radii of the escribed circles opposite to the angles $B$ and $C$ respectively.

Formulae for $r_1, r_2$ and $r_3$
1. $r_1=\frac{\Delta}{s-a}, r_2=\frac{\Delta}{s-b}, \quad r_3=\frac{\Delta}{s-c}$
2. $r_1=s \tan \frac{A}{2}, \quad r_2=s \tan \frac{B}{2}, \quad r_3=s \tan \frac{C}{2}$
3. $r_I=4 R \sin \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}$ $r_2=4 R \cos \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2}$ $r_3=4 R \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}$

Properties of Escribed Circle

1. Escribed circle is tangent to one side of the triangle.

2. Radius is called as exradius.

3. The center is called an excenter.

Exradius and Excenter are calculated as:

1. Semi-Perimeter: $s=\frac{a+b+c}{2}$
2. Area Using Heron's Formula: $A=\sqrt{s(s-a)(s-b)(s-c)}$
3. Exradius: $r_a=\frac{A}{s-a}, \quad r_b=\frac{A}{s-b}, \quad r_c=\frac{A}{s-c}$
4. Excenter Coordinates:

$I_a=\left(\frac{-a A_x+b B_x+c C_x}{-a+b+c}, \frac{-a A_y+b B_y+c C_y}{-a+b+c}\right)$

Recommended Video Based on Escribed Circle of Triangle

Solved Examples Based on Escribed Circle of Triangle

Example 1: Find the value of $\frac{r_1+r_2+r_3-r}{2 R}$ where $r_1, r_2, r_3$ are radii of ex-circles and $r$ and $R$ is the radii of the incentre and circumcentre

1) $0$

2) $1$

3) $2$

4) $4$

Solution

$\begin{aligned} & r_1+r_2+r_3-r=\frac{\Delta}{(s-a)}+\frac{\Delta}{(s-b)}+\frac{\Delta}{(s-c)}-\frac{\Delta}{(s)} \\ & =\Delta\left[\frac{s-b+s-a}{(s-a)(s-b)}+\frac{(s-s+c)}{(s)(s-c)}\right] \\ & =\Delta\left[\frac{c}{(s-a)(s-b)}+\frac{(c)}{(s)(s-c)}\right] \\ & =\Delta c\left[\frac{s(s-c)+(s-a)(s-b)}{s(s-a)(s-b)(s-c)}\right] \\ & =\Delta c\left[\frac{\left.2 s^2-s(a+b+c)+a b\right)}{\Delta^2}\right] \\ & =\frac{c}{\Delta}(a b) \\ & =\frac{a b c}{\Delta} \\ & =4 R \\ & \Rightarrow \frac{r_1+r_2+r_3-r}{2 R}=2\end{aligned}$

Hence, the answer is the option (3).

$\text { Example 2: In triangle } \mathrm{ABC} \text { if } r_1, r_2, r_3 \text { are radii of ex-circles and } r_2=r_1+r_3+r \text { then which of following is true? }$

1) $A$ is a acute angle

2) $B $ is a right angle

3) $C$ is a acute angle

4) All of above

Solution

$\begin{aligned} & r_2=r_1+r_3+r \\ & r_2-r=r_1+r_3 \\ & \frac{\Delta}{(s-b)}-\frac{\Delta}{(s)}=\frac{\Delta}{(s-a)}+\frac{\Delta}{(s-c)} \\ & \frac{\Delta b}{s(s-b)}=\frac{\Delta(2 s-a-c)}{(s-a)(s-c)} \\ & s(s-b)=(s-a)(s-c) \\ & s^2-s b=s^2-s(a+c)+a c \\ & s(a+c-b)=a c \\ & (a+b+c)(a+c-b)=2 a c \\ & (a+c)^2-b^2=2 a c \\ & a^2+c^2=b^2\end{aligned}$

Hence, it is a right-angled triangle with a right angle at $B$.

Hence, the answer is the option (4).

Example 3: In a triangle with sides $a, b, c, r_1>r_2>r_3$ (which are the ex-radii) then:
1) $a>b>c$
2) $a<b<c$
3) $a>b$ and $b<c$
4) $a<b$ and $b>c$

Solution

As learned,

The ex-radii of a triangle are given by

$r_1=\frac{\Delta}{s-a} r_2=\frac{\Delta}{s-b} r_3=\frac{\Delta}{s-c}$

where, $r_1, r_2$, and $r_3$ are the ex-radii of the triangle for the ex-circles in front of vertices $A, B$, and $C$ respectively.

$\begin{aligned}
& r_1>r_2>r_3 \\
\Rightarrow & \frac{\Delta}{s-a}>\frac{\Delta}{s-b}>\frac{\Delta}{s-c}
\end{aligned}$

Now, as $\Rightarrow s-a<s-b<s-c$

$\Rightarrow a>b>c$

Hence, the answer is the option (1).

Example 4: If $I_1, I_2, I_3$ are the centers of escribed circles of $\triangle A B C$, the the area of the triangle $I_1, I_2, I_3$ is
1) 1
2) -1
3) $\frac{a b c}{2 r}$
4) $-\frac{a b c}{2 r}$

Solution

$I_1, I_2, I_3$ are the centers of escribed circles of $\triangle A B C$

$\text { Area }=\frac{I_1 I_2 \times I_2 I_3 \times I_1 I_3}{4 R}$

Applying the formula to get,

$\begin{aligned}
& \text { Area }=\frac{\left(4 R \cos \frac{A}{2}\right) \times\left(4 R \cos \frac{B}{2}\right) \times\left(4 R \cos \frac{C}{2}\right)}{2 \times 4 R} \\
& \text { Area }=8 R^2 \cos \frac{a}{2} \cos \frac{b}{2} \cos \frac{c}{2} \\
& \text { Area }=\frac{8 R^2 \sin A \sin B \sin C}{8 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}} \\
& \text { Area }=\frac{R^2 a b c}{8 R^3 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}} \\
& \text { Area }=\frac{a b c}{2\left(4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)} \\
& \text { Area }=\frac{a b c}{2 r}
\end{aligned}$

Hence, the answer is the option 3.