Height And Distance: Definition & Formula

What are Height and Distance?

It is not possible to measure every distance using a measuring tape, for instance, the altitude of an aeroplane at a certain time, the distance of a ship from a lighthouse, the height of a hill (distance between its foot and summit), the distance between two celestial objects, etc. To measure such distances, scientists developed the method of trigonometric ratios. When dealing with heights and depths, we have to measure two types of angles (above and below the observer's eye level). Trigonometric ratios are useful to solve problems regarding height and distances around us in real life.

How to Find Heights and Distances?

Before solving problems on heights and distances, it is important to understand the basic terms used in trigonometry. These concepts form the foundation for applying trigonometric ratios to real-life situations such as measuring the height of a tower, distance of a ship from the shore, or length of a shadow. To measure the heights and distances of different objects, we use trigonometric ratios.

What is the Angle of Elevation?

The angle of elevation is the angle formed between the horizontal line of sight and the line drawn upward towards an object above the observer’s eye level. For example, if you look at the top of a building from the ground, the angle your line of sight makes with the horizontal ground is called the angle of elevation. This concept is frequently used in height and distance questions to calculate unknown heights and distances.

The student is looking at the top of the tower. The line AC drawn from the eye of the student to the top of the tower is called the line of sight. The angle BAC, so formed by the line of sight with the horizontal, is called the angle of elevation of the top of the tower from the eye of the student. It is called the angle of elevation because the object is above the observer’s eye level.

Here $α$ is the angle of elevation.

What is the Angle of Depression?

The angle of depression is the angle formed between the horizontal line of sight and the line drawn downward towards an object below the observer’s eye level. For instance, when an observer at the top of a lighthouse looks down at a ship in the sea, the angle formed is the angle of depression. Many height and distance problems involve both angle of elevation and angle of depression for accurate measurement.

If the object is below the observer’s eye level, the angle between the horizontal line and the line of sight is called the angle of depression of the object.

Here $β$ is the angle of depression.

The angles of elevation and depression are usually measured by a device called an Inclinometer or Clinometer.

Line of Sight and Horizontal Line

The line of sight is an imaginary straight line drawn from the observer’s eye to the object being viewed. The horizontal line is the line that runs parallel to the ground from the observer’s eye level. In trigonometry heights and distances problems, the angle of elevation and the angle of depression are always measured from this horizontal line. Understanding this relationship is crucial for correctly applying trigonometric ratios like sine, cosine, and tangent.

Heights and Distances Formulas

In trigonometry, problems on heights and distances are solved using specific formulas based on right triangles. These formulas use trigonometric ratios such as $\sin \theta$, $\cos \theta$, and $\tan \theta$.

Case 1: In this case, we can observe the following:

• Height of a tower, hill, or building

• Distance of an object from the foot of the tower, hill, or building and sometimes the shadow of them

• The angle of elevation or the angle of depression

Any two of the above three parameters will be provided in the question. This type of problem can be solved using the formulas given below.

In the right triangle $ABC$,

$\begin{aligned} & \sin \theta=\text { Opposite } / \text { Hypotenuse }=\mathrm{AB} / \mathrm{AC} \\ & \cos \theta=\text { Adjacent } / \text { Hypotenuse }=\mathrm{BC} / \mathrm{AC} \\ & \tan \theta=\text { Opposite } / \text { Adjacent }=\mathrm{AB} / \mathrm{BC}\end{aligned}$

Case 2: In this case, we can deal with different illustrations. One of the commonly solved problems is about the movement of an observer. If the observer moves toward the objects like a tower, building, hill, etc., then the angle of elevation increases. The angle of elevation decreases when the observer moves away from the object. Here, the distance moved by the observer can be found using the formula given below:

In the right triangle given below, $d$ is the distance between $C$ and $D$.

$d = h(cot x – cot y)$

Case 3: There is another case where two different situations happen at the same. In this case, we get similar triangles with the same angle of elevation or angle of depression. These types of problems can be solved with the help of formulas related to similar triangles.

In the right triangle $ABC, DE || AB,$

Here, triangles $ABC$ and $EDC$ are similar.
Using Thales or BPT theorem we can write the ratio of sides as:
$AB/ED = BC/DC$

Basic Trigonometric Formulas

The fundamental trigonometric ratios applied in height and distance problems are:

• $\sin \theta = \dfrac{\text{Opposite Side}}{\text{Hypotenuse}}$

• $\cos \theta = \dfrac{\text{Adjacent Side}}{\text{Hypotenuse}}$

• $\tan \theta = \dfrac{\text{Opposite Side}}{\text{Adjacent Side}}$

These relations are the base for finding heights, lengths, or distances in real-life situations.

Standard Results for Angle of Elevation and Depression

For a right triangle formed with an object and the line of sight:

• If the observer looks upward, angle of elevation is used:
  $\tan \theta = \dfrac{\text{Height of Object}}{\text{Horizontal Distance}}$

• If the observer looks downward, angle of depression is used:
  $\tan \theta = \dfrac{\text{Vertical Height}}{\text{Horizontal Distance}}$

These direct formulas help in solving typical exam problems quickly.

Application of Right Triangles

Every height and distance problem reduces to a right triangle where Pythagoras’ theorem and trigonometric ratios are applied:

• By Pythagoras: $a^2 + b^2 = c^2$

• By trigonometry: $\tan \theta = \dfrac{\text{Perpendicular}}{\text{Base}}$

For example, if the height of a tower is $h$ and the distance of the observer is $d$, then:
$\tan \theta = \dfrac{h}{d}$, hence $h = d \cdot \tan \theta$.

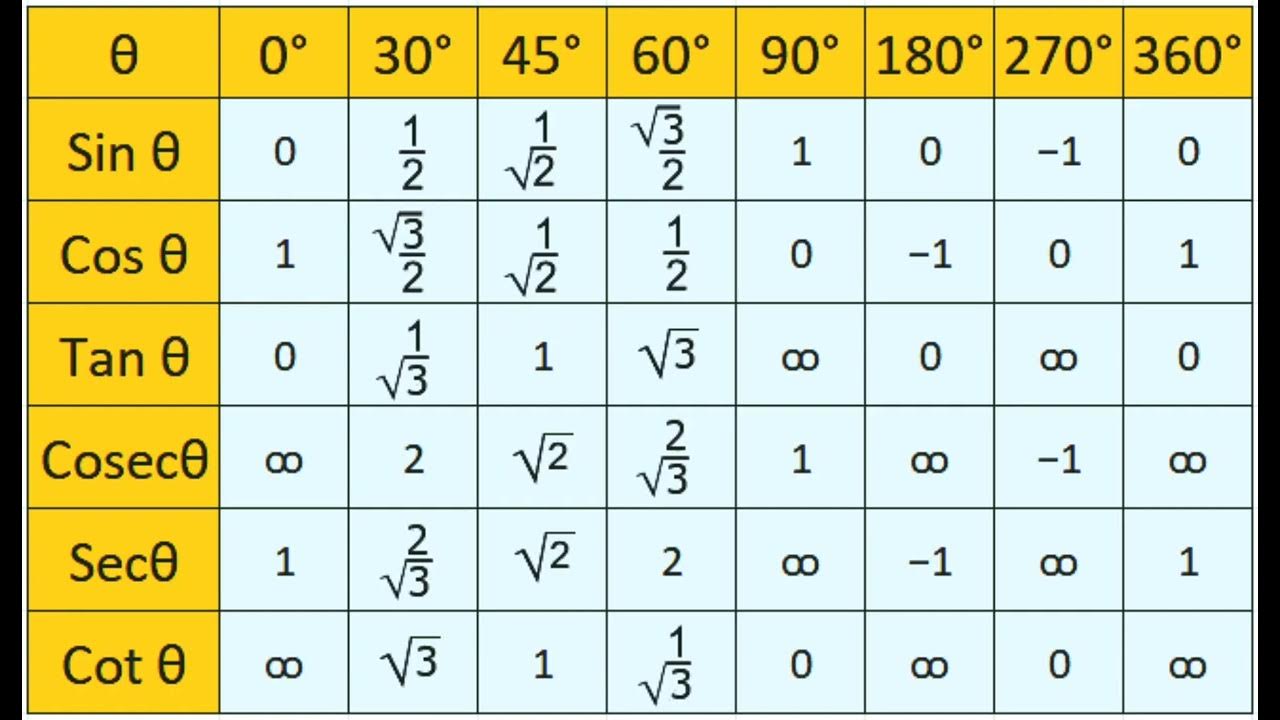
Trigonometric Ratios of Standard Angles

Solved Examples based on Height and Distance

Example 1: In the figure, $\theta_1+\theta_2=\frac{\pi}{2}$ and $\sqrt{3}(\mathrm{BE})=4(\mathrm{AB})$. If the area of $\triangle \mathrm{CAB}$ is $2 \sqrt{3}-3$ unit $^2$, when $\frac{\theta_2}{\theta_1}$ is the largest, then the perimeter (in units) of $\triangle \mathrm{CED}$ is equal to $\qquad$

Solution:

$\sqrt{3}\ BE = 4\ AB$
Ar$(\triangle CAB) = 2\sqrt{3}-3$
$\frac{1}{2} x^2 \tan \theta_1 = 2\sqrt{3}-3$
$BE = BD + DE$
$BE = x (\tan \theta_1 + \tan \theta_2)$
$BE = AB (\tan \theta_1 + \cot \theta_1)$
$\frac{4}{\sqrt{3}} (\tan \theta_1 + \cot \theta_1) \Rightarrow \tan \theta_1 = \sqrt{3}, \frac{1}{\sqrt{3}}$
$\theta_1 = \frac{\pi}{6}, \ \theta_2 = \frac{\pi}{3}$
$\theta_1 = \frac{\pi}{3}, \ \theta_2 = \frac{\pi}{6}$
As $\theta_2/\theta_1$ is largest, therefore $\theta_1 = \frac{\pi}{6}, \ \theta_2 = \frac{\pi}{3}$
Therefore, $x^2 = \frac{(2\sqrt{3}-3) \times 2}{\tan \theta_1} = \frac{\sqrt{3}(2-\sqrt{3}) \times 2}{\tan \frac{\pi}{6}}$
$x^2 = 12 - 6\sqrt{3} = (3-\sqrt{3})^2$
Perimeter of $\triangle C E D$
$=C D+D E+C E$
$=3 \sqrt{3}+(3-\sqrt{3}) \sqrt{3}+(3-\sqrt{3}) \times 2=6$
Hence, the answer is $6$.

Example 2: The angle of elevation of the top $P$ of a tower from the feet of one person standing due South of the tower is $45^{\circ}$ and from the feet of another person standing due west of the tower is $30^{\circ}$. If the height of the tower is $5$ meters, then the distance ( in meters) between the two persons is equal to

Solution:

Tower $AB = 5\ \text{m}$
$ \angle APB = 45^\circ $
$ \angle PAB = 90^\circ $

$\tan 45^{\circ}=\frac{\mathrm{AB}}{\mathrm{AP}}$
$1=\frac{\mathrm{AB}}{\mathrm{AP}}$
$\mathrm{AP}=5 \mathrm{~m}$

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{AQ}}$
$\frac{1}{1 \sqrt{3}}=\frac{5}{\mathrm{AQ}}$
$\mathrm{AQ}=5 \sqrt{3}$

$ AP^2 + AQ^2 = PQ^2 $
$ PQ^2 = 5^2 + (5\sqrt{3})^2 $
$ PQ^2 = 25 + 75 = 100 $
$ PQ = 10\ \text{cm} $

Hence, the answer is $ 10 $

Example 3: From the top $A$ of a vertical wall $A B$ of height 30 m , the angles of depression of the top $P$ and bottom $Q$ of a vertical tower $P Q$ are $15^{\circ}$ and $60^{\circ}$ respectively, $B$ and $Q$ are on the same horizontal level. If $C$ is a point on $A B$ such that $C B=P Q$, then the area (in m 2 ) of the quadrilateral $B C P Q$ is equal to :

Solution:

$ \frac{AB}{BQ} = \tan 60^\circ $
$ BQ = \frac{30}{\sqrt{3}} = 10\sqrt{3} = y $

Consider $ \triangle ACP $

$ \frac{AC}{CP} = \tan 15^\circ \Rightarrow \frac{30 - x}{y} = 2 - \sqrt{3} $
$ 30 - x = 10\sqrt{3} (2 - \sqrt{3}) $
$ 30 - x = 20\sqrt{3} - 30 $
$ x = 60 - 20\sqrt{3} $

Area $= x \cdot y = (60 - 20\sqrt{3}) \cdot 10\sqrt{3} = 600(\sqrt{3} - 1)$

Hence, the answer is $ 600(\sqrt{3} - 1) $

Example 4: Let a vertical tower $AB$ of height $2 h$ stands on horizontal ground. From a point $P$ on the ground, a man can see up to the height h of the tower with an angle of elevation $2 \alpha$. When from $P$ , he moves a distance d in the direction of $\overrightarrow{A P}$, he can see the top $B$ of the tower with an angle of elevation $\alpha$. If $\mathrm{d}=\sqrt{7} \mathrm{~h}$, then $\tan \alpha$ is equal to

Solution:

$ \tan 2\alpha = \frac{h}{x} $
$ \tan \alpha = \frac{2h}{x + \sqrt{7} h} $
$ \tan \alpha = \frac{2h}{h \cot 2\alpha + \sqrt{7} h} $
$ \tan \alpha = \frac{2}{\frac{1 - \tan^2 \alpha}{2 \tan \alpha} + \sqrt{7}} $
Put $ \tan \alpha = t $ and simplify
$ \Rightarrow \tan \alpha = \sqrt{7} - 2 $
Hence, the answer is $ \sqrt{7} - 2 $

Example 5: A tower $PQ$ stands on a horizontal ground with base $Q$ on the ground. Point $R$ divides the tower in two parts such that $\mathrm{QR}=15 \mathrm{~cm}$. If from a point A on the ground, the angle of elevation of $R$ is $60^{\circ}$ and the part $P R$ of the tower subtends an angle of $15^{\circ}$ at $A$, then the height of the tower is Point $R$ divides the tower in two parts such that $\mathrm{QR}=15 \mathrm{~m}$. If from a point $A$ on the ground, the angle of elevation of $R$ is $60^{\circ}$ and the part $P R$ of the tower subtends an angle of $15^{\circ}$ at $A$, then the height of the tower is :

Solution:

$ \frac{15}{\mathrm{AQ}} = \tan 60^\circ $
$ \frac{15 + x}{\mathrm{AQ}} = \tan 75^\circ $
$ \frac{(1)}{(2)} \Rightarrow x = 10 \sqrt{3} $
so, $\mathrm{PQ} = 5(2 \sqrt{3} + 3) \mathrm{m}$
Hence, the answer is $5(2 \sqrt{3} + 3) \mathrm{m}$

List of Topics Related to Height and Distance

Below are the important topics related to Height and Distance in trigonometry, which include the key concepts, formulas, and applications used to solve real-world measurement problems effectively.

NCERT Resources

Below are the NCERT resources for Class 11 Trigonometric Functions, including detailed notes, solved examples, and exemplar solutions to help students strengthen their understanding of heights and distances.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3- Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3- Trigonometric Functions

Practice Questions based on Height and Distance

Here are some key practice problems on heights and distances to help strengthen your understanding of angles of elevation, depression, and real-life trigonometry applications.

Height And Distance - Practice Question MCQ

You can practice the related questions from the links shared below: