Horizontal and Vertical Ellipse: Definition and Examples

Edited By Komal Miglani | Updated on Oct 05, 2024 06:25 PM IST

An ellipse is the set of all points (x, y) in a plane such that the sum of their distances from two fixed points is a constant. The line that passes through the focus and is perpendicular to the directrix is called the major axis (focal axis) of the ellipse. We have another axis of the ellipse called the minor axis. So, the ellipse has 2 axes one major axis and another minor axis. In real life, we use Ellipse in race tracks, architectural design, mirrors, and celestial orbits.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

What is Ellipse?
Vertical Ellipse
Solved Examples Based on Horizontal and Vertical Ellipse

Horizontal and Vertical Ellipse: Definition and Examples

In this article, we will cover the concept of Horizontal and Vertical Ellipse. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of twenty questions have been asked on JEE MAINS( 2013 to 2023) from this topic including two in 2021, and one in 2022.

What is Ellipse?

The locus of a point moves in a plane such that the ratio of the distance from a fixed point (focus) to the distance from a fixed line (directrix) is constant. The constant is known as eccentricity e and for ellipse 0 < e < 1.

Horizontal Ellipse

When the major axis is along the X-axis and the minor axis is along the Y-axis, i.e. a > b, it is called a horizontal ellipse.

the length of the major axis is 2a

the length of the minor axis is 2b

The foci are S (0, ae) and S’(0, -ae)

Vertical Ellipse

When the major axis is along the Y-axis and the minor axis is along the X-axis, i.e. b > a, it is called a vertical ellipse.

Then, AA’ = 2a and BB’ = 2b

the length of the major axis is 2b

the length of the minor axis is 2a

The foci are S (0, be) and S’(0, -be)

The equation of directrix MZ and M’Z’ are $
y=\frac{b}{e} \text { and } y=-\frac{b}{e}
$

Equation	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ; a>b$	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ; a<b$
Graph
Centre	(0, 0)	(0, 0)
Vertices	$( \pm \mathrm{a}, 0)$	$(0, \pm \mathrm{b})$
Length of Major Axis	$2a$	$2b$
Length of Minor Axis	$2b$	$2a$
Foci	$( \pm a e, 0)$	$(0, \pm \mathrm{be})$
Distance b/w foci	$2ae$	$2be$
Equation of Directrices	$\mathrm{x}= \pm \frac{\mathrm{a}}{\mathrm{e}}$	$y= \pm \frac{b}{e}$
Distance b/w Directrices	$\frac{2 \mathrm{a}}{\mathrm{e}}$	$\frac{2 b}{e}$
Eccentricity, e	$e=\sqrt{1-\frac{b^2}{a^2}}$	$e=\sqrt{1-\frac{a^2}{b^2}}$
Length of Latusrectum	$\frac{2 b^2}{a}$	$\frac{2 \mathrm{a}^2}{\mathrm{~b}}$
Endpoint of Latusrectum	$\left( \pm \mathrm{ae}, \pm \frac{\mathrm{b}^2}{\mathrm{a}}\right)$	$\left( \pm \frac{a^2}{b}, \pm b e\right)$
Focal radii	$S P+S^{\prime} P=2 a$	$S P+S^{\prime} P=2 b$
Parametric coordinates	$(a \cos \theta, b \sin \theta) \quad 0 \leq \theta \leq 2 \pi$	$(a \cos \theta, b \sin \theta) \quad 0 \leq \theta \leq 2 \pi$
Tangent at vertices	$\mathrm{x}= \pm \mathrm{a}$	$y= \pm b$

Solved Examples Based on Horizontal and Vertical Ellipse

Example 1: Let $E_1: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a>\mathrm{b}$. Let $E_2$ be another ellipse such that it touches the endpoints of the major axis of $E_1$ and the foci of $E_2$ are the endpoints of the minor axis of $\mathrm{E}_1$. If $\mathrm{E}_1$ and $\mathrm{E}_2$ have the same eccentricities, then its value is : [JEE MAINS 2021]

Solution

$
\begin{aligned}
&\text { As per the question, }\\
&\begin{aligned}
& b=c e_2 \text { and } e_1=e_2 \\
\Rightarrow & b=c e_2 \text { and } e_1^2=e_2^2 \\
\Rightarrow & b=c e_2 \text { and } 1-\frac{b^2}{a^2}=1-\frac{a^2}{c^2} \\
\Rightarrow & b=c e_2 \quad \text { and } \quad \frac{b^2}{a^2}=\frac{a^2}{c^2} \\
\Rightarrow & b=c e_2 \quad \text { and } \quad c^2=\frac{a^4}{b^2} \\
\Rightarrow & c=\frac{b}{e_2} \quad \text { and } \quad c=\frac{a^2}{b} \\
\Rightarrow & \frac{b}{e_2}=\frac{a^2}{b} \\
\Rightarrow & e_2=\frac{b^2}{a^2} \\
\Rightarrow & e_2=1-e_1^2 \\
\Rightarrow & e_1=1-e_1^2 \\
\Rightarrow & e_1^2+e_1-1=0 \\
\Rightarrow & e_1=\frac{\sqrt{5}-1}{2}
\end{aligned}
\end{aligned}
$

Hence, the correct answer is $\frac{-1+\sqrt{5}}{2}$
Example 2: Let $\mathrm{S}=\left\{(\mathrm{x}, \mathrm{y}) \in \mathbb{N} \times \mathbb{N}: 9(\mathrm{x}-3)^2+16(\mathrm{y}-4)^2 \leq 144\right\}$ and $\mathrm{T}=\left\{(\mathrm{x}, \mathrm{y}) \in \mathbb{R} \times \mathbb{R}:(\mathrm{x}-7)^2+(\mathrm{y}-4)^2 \leq 36\right\}$. Then $\mathrm{n}(\mathrm{S} \cap \mathrm{T})$ is equal to $\qquad$
[JEE MAINS 2022]
Solution

For $\mathrm{x}=1 \Rightarrow(1,4)$
For $\mathrm{x}=2 \Rightarrow(2,4),(2,5),(2,3),(2,6),(2,2)$
For $\mathrm{x}=3 \Rightarrow(3,4),(3,5),(3,3),(3,6),(3,2)(3,7),(3,1)$
For $\mathrm{x}=4 \Rightarrow(4,4),(4,5),(4,3),(4,6),(4,2)$
For $\mathrm{x}=5 \Rightarrow(5,4),(5,5),(5,3),(5,2),(5,6)$
For $\mathrm{x}=6 \Rightarrow(6,4),(6,3),(6,5)$
For $\mathrm{x}=7 \Rightarrow(7,4)$
$\therefore$ Total 27 common points
Ans:27

Example 3: If $x^2+9 y^2-4 x+3=0, x, y \in \mathbb{R}$, then x and $y$ respectively lie in the intervals :
[JEE MAINS 2021]
Solution: To find the Range of x , make quadratic in y

$
\begin{aligned}
& 9 y^2+x^2-4 x+3=0 \\
& D \geq 0 \\
& \Rightarrow 0-4 \times 9 \times\left(x^2-4 x+3\right) \geq 0 \\
& \Rightarrow(x-1)(x-3) \leq 0 \Rightarrow x \epsilon[1,3]
\end{aligned}
$
To Find the Range of y , make quadratic in x

$
\begin{aligned}
& x^2-4 x+9 y^2+3=0 \\
& D \geq 0 \\
& \Rightarrow 4^2-4 \times\left(9 y^2+3\right) \geq 0 \Rightarrow 9 y^2-1 \leq 0 \\
& \Rightarrow(3 y-1)(3 y+1) \leq 0 \Rightarrow y \epsilon\left[\frac{-1}{3}, \frac{1}{3}\right]
\end{aligned}
$
Hence, the answer is $[1,3]$ and $\left[-\frac{1}{3}, \frac{1}{3}\right]$

Example 4: What are the coordinates of the midpoints of the ellipse $x^2+4 y^2-6 x+40 y=0$
Solution: We know that the center of the Ellipse is the mid-point of the two foci of the ellipse.

$
\begin{aligned}
& x^2-6 x+4\left(y^2+10 y\right)=0 \\
& x^2-6 x+9+4\left(y^2+10 y+25\right)=100+9 \\
& (x-3)^2+4(y+5)^2=109
\end{aligned}
$
Centre is $(3,-5)$
Hence, the answer is $(3,-5)$

Example 5: Consider an ellipse, whose center is at the origin and its major axis is along the $x$-axis. If its eccentricity is $\frac{3}{5}$ and the distance between its foci is 6 , then the area (in sq. units) of the quadrilateral inscribed in the ellipse, with the vertices as the endpoints of major and minor axes of the ellipse, is

Solution

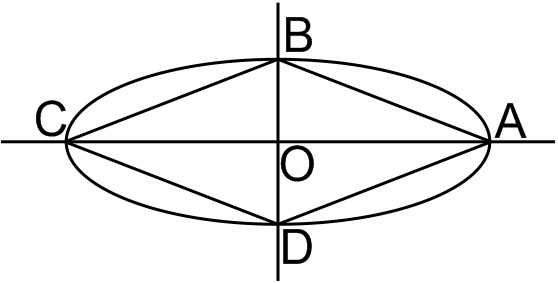
Given

$
e=\frac{3}{5}
$

and

$
2 a e=6 \Rightarrow a e=3
$
Hence $a=5$

$
b^2=a^2\left(1-e^2\right) \Rightarrow b=4
$
Area of quadrilateral $\mathrm{ABCD}=4 \operatorname{Ar}(\Delta A O B)$

$
\begin{aligned}
& =4 \times \frac{1}{2} \times a \times b \\
& =4 \times \frac{1}{2} \times 5 \times 4 \\
& =40
\end{aligned}
$
Hence, the answer is 40

Summary

Horizontal and vertical ellipses represent distinct orientations of the same geometric shape, each characterized by unique equations and positional relationships of their vertices and co-vertices. They exhibit distinct visual characteristics and mathematical properties. Knowledge of different orientations of ellipses is necessary for analyzing the properties of ellipses.