In-Circle and In-Centre: Formula, Properties and Examples

A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. A triangle has six main elements, three sides, and three angles. There are many properties of triangles like circumcentre, incentre, centroid, orthocentre, etc. The incircle is the largest inscribed circle of a triangle. In real life, we use encircles in the design of gears.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is In-Circle and In-Centre?
2. In Radius Formula
3. Derivation of In Radius
4. Length of tangent from vertices to the In-circle
5. Distance of incentre from the vertices of the triangle
6. Solved Examples Based on In-Circle and In-Centre

In this article, we will cover the concept of the Circumcircle. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of five questions have been asked on this concept including one in 2021.

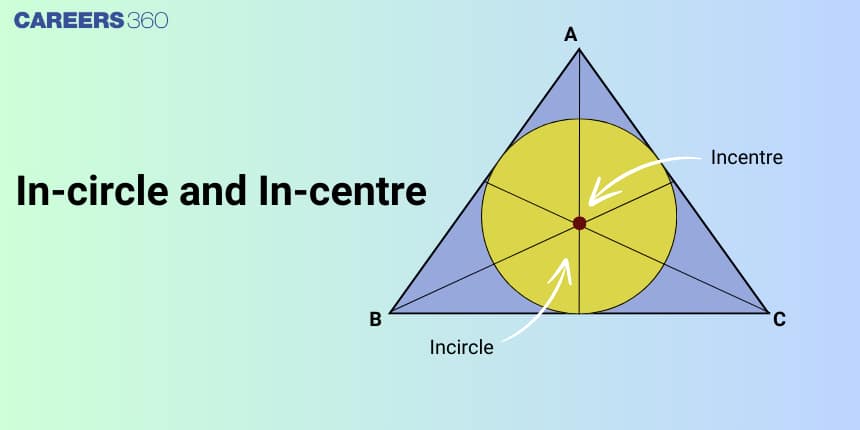
What is In-Circle and In-Centre?

The incircle or circle inscribed in a triangle is the largest circle contained in the triangle; it touches (or it is tangent to) the three sides of the triangle. The center / of the incircle is called the incentre of the triangle. The radius of the incircle is called inradius and is usually denoted by r .

Incenter of a Triangle Properties

Below are the few important properties of triangles’ incenter.

1. If I is the incenter of the triangle ABC (as shown in the above figure), then line segments AE and AG, CG and CF, BF and BE are equal in length, i.e. AE = AG, CG = CF and BF = BE.
2. If I is the incenter of the triangle ABC, then ∠BAI = ∠CAI, ∠BCI = ∠ACI and ∠ABI = ∠CBI (using angle bisector theorem).
3. The sides of the triangle are tangents to the circle, and thus, EI = FI = GI = r known as the inradii of the circle or radius of incircle.
4. If s is the semiperimeter of the triangle and r is the inradius of the triangle, then the area of the triangle is equal to the product of s and r, i.e. A = sr.
5. The triangle’s incenter always lies inside the triangle.

The point of intersection of the internal angle bisectors of a triangle is called the in-center of the triangle. Also, a circle that can be inscribed within a triangle such that it touches each side of the triangle internally is called an incircle triangle. Its center is the center of the given triangle. The in-center of a triangle is denoted by l .

How to Construct the Incenter of a Triangle?

The construction of the incenter of a triangle is possible with the help of a compass. Here are the steps to construct the incenter of a triangle:

• Step 1: Place one of the compass's ends at one of the triangle's vertex. The other side of the compass is on one side of the triangle.
• Step 2: Draw two arcs on two sides of the triangle using the compass.
• Step 3: By using the same width as before, draw two arcs inside the triangle so that they cross each other from the point where each arc crosses the side.
• Step 4: Draw a line from the vertex of the triangle to where the two arcs inside the triangle cross.
• Step 5: Repeat the same process from the other vertex of the triangle.
• Step 6: The point at which the two lines meet or intersect is the incenter of a triangle.

In Radius Formula

The radius of the in-circle of a triangle is called the in-radius and it is denoted by ‘r’.

1. In - radius, $r$ is given by $=\frac{\Delta}{s}$
2. $r=(s-a) \tan \frac{\mathrm{A}}{2}=(s-b) \tan \frac{\mathrm{B}}{2}=(s-c) \tan \frac{\mathrm{C}}{2}$
3. $r=4 \mathrm{R} \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}$

Derivation of In Radius

1. Consider the triangle, $ABC$

We know that, the area of $ABC =$ area of $IBC +$ area of $IBA +$ area of $ICA$

$\begin{aligned} \Delta & =\frac{1}{2} a r+\frac{1}{2} b r+\frac{1}{2} c r \\ & =\frac{1}{2} r(a+b+c) \\ & =\frac{1}{2} r(2 s) \quad[\because 2 s=a+b+c] \\ & =r s\end{aligned}$

2. From the half-angle formula of tangent

$\tan \frac{\mathrm{A}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{s}(\mathrm{s}-\mathrm{a})}}$

Multiply both sides with ( $s$ - a)

$\begin{aligned}
(s-a) \tan \frac{\mathrm{A}}{2} & =(s-a) \sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{s}(\mathrm{s}-\mathrm{a})}} \\
& =\sqrt{\frac{(s-a)(s-b)(s-c)}{s}} \\
& =\frac{\sqrt{s(s-a)(s-b)(s-c)}}{s} \\
& =\frac{\Delta}{s}=r \quad[\because \Delta=\sqrt{\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})]}
\end{aligned}$
In a similar fashion, other formulae can be proved
3. From the half-angle formula of sine

$\begin{aligned}
& \sin \frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{b c}} \\
& \sin \frac{B}{2}=\sqrt{\frac{(s-a)(s-c)}{a c}} \\
& \sin \frac{C}{2}=\sqrt{\frac{(s-a)(s-b)}{a b}}
\end{aligned}$

So,
$\left[\right.$ We are using the fact that $\Delta=\frac{\mathrm{abc}}{4 \mathrm{R}}$ and $\left.\Delta=\sqrt{s(s-a)(s-b)(s-c)}\right]$

$\begin{aligned}
& 4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}=4 R \sqrt{\frac{(s-b)(s-c)}{b c}} \sqrt{\frac{(s-a)(s-c)}{a c}} \sqrt{\frac{(s-a)(s-b)}{a b}} \\
& =4 \mathrm{R} \frac{(s-a)(s-b)(s-c)}{a b c} \\
& =\frac{4 \mathrm{R}}{\mathrm{abc}} \frac{s(s-a)(s-b)(s-c)}{s} \\
& =\frac{1}{\Delta} \frac{\Delta^2}{\mathrm{~s}}=\frac{\Delta}{\mathrm{s}}=\mathrm{r}
\end{aligned}$

Length of tangent from vertices to the In-circle

In the figure, $\mathrm{AF}=\mathrm{AE}=\mathrm{x}$

$
\begin{aligned}
& B F=B D=y \\
& C E=C D=z \\
& A B+B C+C A=A F+F B+B D+D C+C E+E A \\
& a+b+c=2 x+2 y+2 z \\
& 2 s=2 x+2 y+2 z \\
& s=x+y+z
\end{aligned}
$

Now, $y+z=B C=a$. So, $x-s=a$
Similarly, $y=s-b$ and $z=s-c$
Thus, lengths of tangents to incircle from the vertice $A, B$, and $C$ are(s-a),(sb), and (s-c) respectively

Distance of incentre from the vertices of the triangle

$\mathrm{Al}=\frac{r}{\sin \frac{A}{2}}$

Similarly, $\mathrm{BI}=\frac{r}{\sin \frac{B}{2}}$ and $\mathrm{CI}=\frac{r}{\sin \frac{C}{2}}$
Length of angle Bisector

$\mathrm{AP}=\frac{2 b c}{b+c} * \cos \frac{A}{2}$

Similarly, $\mathrm{BQ}=\frac{2 a c}{a+c} * \cos \frac{B}{2}$ and $\mathrm{CR}=\frac{2 a b}{b+a} * \cos \frac{C}{2}$

Recommended Video Based on In-Circle and In-Centre

Solved Examples Based on In-Circle and In-Centre

Example 1: To find the coordinates of the incenter of a triangle whose vertices are given as $A(-36,15) B(0,0)$, and $C(20,15)$.
Solution: Given that,

$\begin{aligned}
& A(-36,15)=\left(x_1, y_1\right) \\
& B(0,0)=\left(x_2, y_2\right) \\
& C(20,15)=\left(x_3, y_3\right)
\end{aligned}$
To find the length of the sides by using the distance formula,

$\begin{aligned}
& A B=c=\sqrt{(-36-0)^2+(15-0)^2} \\
& A B=c=39 \\
& B C=a=\sqrt{(0-20)^2+(0-15)^2} \\
& B C=a=25 \\
& C A=b=\sqrt{(20+36)^2+(15-15)^2} \\
& C A=b=56
\end{aligned}$

Substituting the values in the incenter formula,

$\begin{aligned} & \left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right) \\ & \left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)=\left(\frac{-900+0+780}{120}, \frac{375+0+585}{120}\right) \\ & \left(\frac{a x_1+b x_2+c x_3}{a+b+c}, \frac{a y_1+b y_2+c y_3}{a+b+c}\right)=(-1,8)\end{aligned}$

Hence, the answer is (-1, 8)

Example 2: Let the centroid of an equilateral triangle $ABC$ be at the origin. Let one of the sides of the equilateral triangle be along the straight line $x + y =3$. If $R$ and $r$ be the radius of circumcircle and incircle respectively of $\triangle A B C$ then $(R+r)$ is equal to:

Solution

$\begin{aligned}
& \mathrm{r}=\mathrm{OM}=\frac{3}{\sqrt{2}} \\
& \sin 30^{\circ}=\frac{1}{2}=\frac{\mathrm{r}}{\mathrm{R}} \\
& \Rightarrow \mathrm{R}=\frac{6}{\sqrt{2}} \\
& \therefore \mathrm{r}+\mathrm{R}=\frac{9}{\sqrt{2}}
\end{aligned}$

Hence, the answer is $\frac{9}{\sqrt{2}}$

Example 3: Let $\mathrm{a}, \mathrm{b}$, and c be the length of sides of a triangle ABC such that $\frac{\mathrm{a}+\mathrm{b}}{7}=\frac{\mathrm{b}+\mathrm{c}}{8}=\frac{\mathrm{c}+\mathrm{a}}{9}$
If $r$ and $R$ are the radius of the incircle and radius of the circumcircle of the triangle $A B C$, respectively, then the value of $\frac{R}{r}$ is equal to:
[JEE MAINS 2022]
Solution
Let $\frac{\mathrm{a}+\mathrm{b}}{7}=\frac{\mathrm{b}+\mathrm{c}}{8}=\frac{\mathrm{c}+\mathrm{a}}{9}=\mathrm{k}$
So $\mathrm{a}+\mathrm{b}=7 \mathrm{k}, \quad \mathrm{b}+\mathrm{c}=8 \mathrm{k}, \quad \mathrm{c}+\mathrm{a}=9 \mathrm{k}$
To solve this we get $\mathrm{a}=4 \mathrm{k}, \mathrm{b}=3 \mathrm{k}, \mathrm{c}=5 \mathrm{k}$ and calculate semi-perimeter $\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2} \Rightarrow \mathrm{s}=6 \mathrm{k}$ we know that $\frac{\mathrm{r}}{\mathrm{R}}=4 \sin \frac{\mathrm{A}}{2} \cdot \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}$

Hence, the answer is $\frac{5}{2}$

$\begin{aligned}
& \Rightarrow \frac{r}{R}=4 \sqrt{\frac{(s-b)(s-c)}{b c}} \times \sqrt{\frac{(s-a)(s-c)}{a c}} \times \sqrt{\frac{(s-a)(s-b)}{a b}} \\
& \Rightarrow \frac{r}{R}=4 \cdot \frac{(s-a)(s-b)(s-c)}{a b c} \\
& \Rightarrow \frac{r}{R}=4 \cdot \frac{(2 k)(3 k)(k)}{(4 k)(3 k)(5 k)} \Rightarrow \frac{r}{R}=\frac{2}{5}
\end{aligned}$

So the value of $\frac{R}{r}=\frac{5}{2}$
Hence, the answer is $\frac{5}{2}$