Independent Event in Probability

Probability is defined as the ratio of the number of favourable outcomes to the total number of outcomes. In probability, an independent event is an important concept. Independent events are those events whose presence doesn't affect others. These operations on the events show us how the values are related. it is important in theoretical mathematics. It is also used in various fields like statistics, finance, etc.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

Events

The set of outcomes from an experiment is known as an Event.
When a die is thrown, sample space $S=\{1,2,3,4,5,6\}$.
Let $A=\{2,3,5\},B=\{1,3,5\},C=\{2,4,6\}$
Here, $A$ is the event of the occurrence of prime numbers, $B$ is the event of the occurrence of odd numbers and $C$ is the event of the occurrence of even numbers.
Also, observe that $A,B$, and $C$ are subsets of $S$.
Now, what is the occurrence of an event?
From the above example, the experiment of throwing a die. Let $E$ denote the event " a number less than $4$ appears". If any of ${}^{\prime }{1}^{\prime }$ or ${}^{\prime }{2}^{\prime }$ or ${}^{\prime }{3}^{\prime }$ had appeared on the die then we say that event E has occurred.
Thus, the event $E$ of a sample space $S$ is said to have occurred if the outcome $\omega$ of the experiment is such that $\omega \in E$. If the outcome $\omega$ is such that $\omega \notin E$, we say that the event $E$ has not occurred.

Independent Events

Two or more events are said to be independent if the occurrence or non-occurrence of any of them does not affect the probability of occurrence or non-occurrence of other events.

If $A$ and $B$ are independent events then $A$ and $\overline{B}$ as well as $\overline{A}$ and $B$ are independent events.

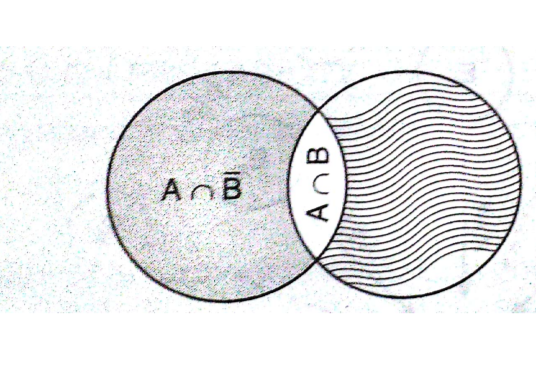
Two events $A$ and $B$ are said to be independent, if

$\begin{array}{rl}& \text{ 1. }P(A\mid B)=P(A)\\ & \text{ 2. }P(B\mid A)=P(B)\end{array}$

A third result can also be obtained for independent events
From the multiplication rule of probability, we have

$P(A\cap B)=P(A)P(B\mid A)$
Now if $A$ and $B$ are independent, then $P(B\mid A)=P(B)$, so

$\text{ 3. }P(A\cap B)=P(A).P(B)$

To show two events are independent, you must show only one of the above three conditions.
If two events are NOT independent, then we say that they are dependent.

With and Without replacement

In some questions, like the ones related to picking some object from a bag with different kinds of objects in it, objects may be picked with replacement or without replacement.

• With replacement: If each object is re-placed in the box after it is picked, then that object has the possibility of being chosen more than once. When sampling is done with replacement, then events are considered to be independent, meaning the result of the first pick will not change the probabilities for the second pick.

• Without replacement: When sampling is done without replacement, the probabilities for the second pick are affected by the result of the first pick. The events are considered to be dependent or not independent.

Difference between Independent events and Mutually Exclusive events

But in the case of independent events $A$ and $B,P(A/B)=P(A)$ [and not 0 as in case of mutually exclusive events], and $P(B/A)=P(B)$ [not 0 ]
Three Independent Events
Three events $A,B$ and $C$ are said to be mutually independent, if

$\begin{array}{ll}& P(A\cap B)=P(A)\cdot P(B)\\ & P(A\cap C)=P(A)\cdot P(C)\\ & P(B\cap C)=P(B)\cdot P(C)\\ \text{ and }& P(A\cap B\cap C)=P(A)\cdot P(B)\cdot P(C)\end{array}$
If at least one of the above is not true for three given events, we say that the events are not independent.

Properties of Independent Event

If $A$ and $B$ are independent events, then

1. $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

$=P(A)+P(B)-P(A)\cdot P(B)$

2. Event ${\underset{―}{A}}^{\prime }$ and $B$ are independent.

$\begin{array}{rl}P(A^{\prime }\cap B)& =P(B)-P(A\cap B)\\ & =P(B)-P(A)P(B)\end{array}$

$\begin{array}{rl}& =P(B)(1-P(A))\\ & =P(B)P\left(A^{\prime }\right)\end{array}$

3. Event $A$ and $B^{\prime }$ are independent.
4. Event $A^{\prime }$ and $B^{\prime }$ are independent.

$\begin{array}{rl}P(A^{\prime }\cap B^{\prime })& =P((A\cup B{)}^{\prime })\\ & =1-P(A\cup B)\\ & =1-P(A)-P(B)+P(A)\cdot P(B)\\ & =(1-P(A))(1-P(B))\\ & =P\left({\underset{―}{A}}^{\prime }\right)P\left(B^{\prime }\right)\end{array}$
these concepts can help in solving gaining deeper insights and contributing meaningfully to real-life problems.

Solved Examples Based on Independent Events

Example 1: Let two fair six-faced dice $A$ and $B$ be thrown simultaneously. If ${\mathrm{E}}_1$ is the event that die $A$ shows up four, ${\mathrm{E}}_2$ is the event that die $B$ shows up two and ${\mathrm{E}}_3$ is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true?
1) $E_1$ and $E_2$ are independent.
2) $E_2$ and $E_3$ are independent.
3) $E_1$ and $E_3$ are independent.

4) $E_1,E_2$ and $E_3$ are independent.

Solution
Independent events -

$\begin{array}{rl}& \therefore P\left(\frac{A}{B}\right)=P(A)\\ & \text{ and }\therefore P(A\cap B)=P(B)\cdot P\left(\frac{A}{B}\right)\\ & \text{ so }\therefore P(A\cap B)=P(A)\cdot P(B)=P(AB)\\ & P\left(E_1\right)=\frac{1}{6},P\left(E_2\right)=\frac{1}{6}\mathrm{\&}P\left(E_3\right)=\frac{1}{2}P(E_1\cap E_2)=\frac{1}{36}P(E_2\cap E_3)=\frac{3}{36}=\frac{1}{12}P(E_1\cap E_3)=\frac{1}{12}P(E_1\cap E_2\cap E_3)=0\\ & P(E_1\cap E_2)=P\left(E_1\right)\cdot P\left(E_2\right)\\ & P(E_2\cap E_3)=P\left(E_2\right)\cdot P\left(E_3\right)\\ & P(E_1\cap E_3)=P\left(E_1\right)\cdot P\left(E_3\right)\\ & \text{ but }\\ & P(E_1\cap E_2\cap E_3)\ne P\left(E_1\right)\cdot P\left(E_2\right)\cdot P\left(E_3\right)\end{array}$
Therefore, $E_1,E_2$ and $E_3$ are not independent.
Hence, the answer is the option 4.

Example 2:Four persons can hit a target correctly with probabilities $\frac{1}{2},\frac{1}{3},\frac{1}{4}$ and $\frac{1}{8}$ respectively. If all hit at the target independently, then the probability that the target would be hit is:

$\text{ 1) }\frac{25}{192}$

2) $\frac{7}{32}$
3) $\frac{1}{192}$
4) $\frac{25}{32}$

Solution
The desired Probability is

$\begin{array}{rl}& =1-(\frac{1}{2}\times \frac{2}{3}\times \frac{3}{4}\times \frac{7}{8})\\ & =\frac{25}{32}\end{array}$
Hence, the answer is the option (4).

Example 3: Let $A$ and $B$ two events such that

$P(\overline{A\cup B})=\frac{1}{6},P(A\cap B)=\frac{1}{4}\text{ and }P(\overline{A})=\frac{1}{4}$

where $\overline{A}$ stands for the complement of the event $A$. Then the events $A$ and $B$ are :
1) independent but not equally likely.
2) independent and equally likely.
3) mutually exclusive and independent.
4) equally likely but not independent.

Solution
Addition Theorem of Probability -

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

In general:

$\begin{array}{rl}& P(A_1\cup A_2\cup A_3\cdots A_n)=\sum _{i=1}^{n}P\left(A_i\right)-\sum _{i<j}^{n}P(A_i\cap A_j)+\sum _{i<j<k}^{n}P(A_i\cap A_j\cap A_k)-\\ & \cdots -(-1{)}^{n-1}P(A_1\cap A_2\cap A_3\cdots \cap A_n)\\ & P(A\cup B)=\frac{5}{6},P(A\cap B)=\frac{1}{4}\\ & P(A)=\frac{3}{4}\mathrm{Let}(B)=x\end{array}$

$\begin{array}{rl}& P(A\cup B)=\frac{5}{6}=\frac{3}{4}+x-\frac{1}{4}\\ & x=\frac{5}{6}-\frac{1}{2}=\frac{1}{3}\end{array}$
$P(A\cap B)+P(A)\cdot P(B)=\frac{1}{4}\text{ independent events }$
Also, $P(A)\ne P(B)$ not equally likely

Example 4: Let A, B and C be three events, which are pair-wise independent and $\overline{E}$ denotes the complement of an event E . If $P(A\cap B\cap C)=0$ and $P(C)>0$ then $P[(\overline{A}\cap \overline{B}\mid C){]}_{\text{is equal to }}$ 1) $P(\overline{A})-P(B)$
2) $P(A)+P(\overline{B})$
3) $P(\overline{A})-P(\overline{B})$
4) $P(\overline{A})+P(\overline{B})$

Solution
Addition Theorem of Probability -

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

$\begin{array}{rl}& \text{ in general: }\\ & \begin{array}{rl}& P(A_1\cup A_2\cup A_3\cdots A_n)=\sum _{i=1}^{n}P\left(A_i\right)-\sum _{i<j}^{n}P(A_i\cap A_j)+\sum _{i<j<k}^{n}P(A_i\cap A_j\cap A_k)-\\ \cdots & -(-1{)}^{n-1}P(A_1\cap A_2\cap A_3\cdots \cap A_n)\end{array}\end{array}$

$\begin{array}{rl}& p(A\cap B)=p(A)\cdot p(B)\\ & P(\overline{A}\cap \overline{B}\mid C)=\frac{P(\overline{A}\cap \overline{B}\cap C)}{P(C)}\end{array}$
$\begin{array}{rl}& P(\overline{A}\cap \overline{B}\mid C)=1-\frac{P(A\cap C)-P(B\cap C)}{P(C)}\\ & =1-p(A)-p(B)\\ & =p(\overline{A})-p(B)\end{array}$

Example 5: For any two events $A$ and $B$ in a sample space

$\text{ 1) }P\left(\frac{A}{B}\right)\ge \frac{P(A)+P(B)-1}{P(B)}\cdot P(B)\ne 0$

does not hold.
2) $P(A\cap \overline{B})=P(A)-P(A\cap B)$ does not hold
3) $P(A\cup B)=1-P(\overline{A})P(\overline{B})$, if A and B are independent
${}_{\text{4) }}P(A\cup B)=1-P(\overline{A})P(\overline{B})$, is A and B are disjoint

Solution
Independent events -

$\begin{array}{rl}& P(A)=P(A\cap \overline{B})\cup (A\cap B)\\ & P(A\cap \overline{B})=P(A)\cdot P(\overline{B})\\ & P(A\cup B)\le 1\Rightarrow P(A\cap B)=PA+P(B)-P(A\cup B)\ge PAP(B)-1\\ & P\left(\frac{A}{B}\right)=\frac{P(A\cap B)}{P(B)}\ge \frac{\{P(A)+P(B)-1\}}{P(B)}\end{array}$

and $1-P(\overline{A})P(\overline{B})=1-(1-P(A))(1-P(B))=P(A)+P(B)-P(A)P(B)$
$=P(A)+P(B)-P(A\cap B)$ (since A and B are independent)

$=P(A\cup B)$
Hence, the answer is an option 3.