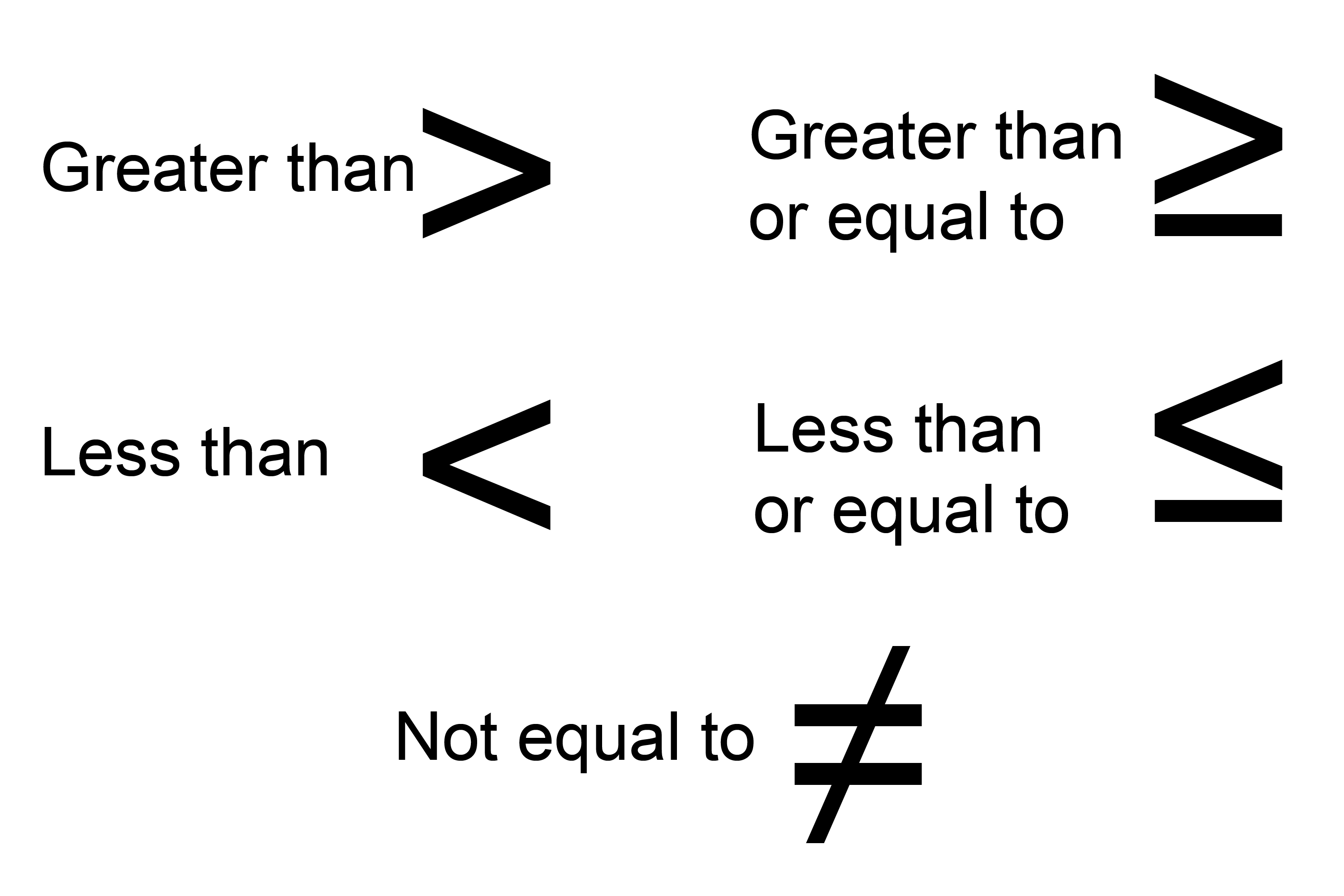Inequalities - Definition, Properties and Solved Linear Inequalities Examples
Inequalities are mathematical expressions showing the relationship between two values, indicating that one value is greater than, less than, or not equal to another. Understanding inequalities is crucial for solving various mathematical problems, from basic arithmetic to advanced calculus.

In this article, we will cover the concepts of the inequalities. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept, including one in 2020.
Inequalities
Inequalities are the relationship between two expressions that are not equal to one another. Symbols denoting the inequalities are <, >, ≤, ≥, and ≠.
- x < 4, “is read as x less than 4”, x ≤ 4, “is read as x less than or equal to 4”.
- Similarly x > 4, “is read as x greater than 4” and x ≥ 4, “is read as x greater than or equal to 4”.
The process of solving inequalities is the same as of equality but instead of equality symbol inequality symbol is used throughout the process.
Inequality Meaning
The meaning of inequality is to say that two things are NOT equal. One of the things may be less than, greater than, less than or equal to, or greater than or equal to the other things.
- p ≠ q means that p is not equal to q
- p < q means that p is less than q
- p > q means that p is greater than q
- p ≤ q means that p is less than or equal to q
- p ≥ q means that p is greater than or equal to q
Types of Inequalities
- Linear Inequalities: Involve linear expressions.
- Example: $2 x+3 \leq 7$
- Quadratic Inequalities: Involve quadratic expressions.
- Example: $x^2-4 x+3>0$
- Polynomial Inequalities: Involve polynomials of degree greater than two.
- Example: $x^3-2 x^2+x-5<0$
- Rational Inequalities: Involve ratios of polynomials.
$\frac{x+1}{x-3} \geq 2$
- Absolute Value Inequalities: Involve absolute value expressions.
- Example: $|x-2| \leq 5$
A few rules that are different from equality rules
- If we multiply or divide both sides of the inequality by a negative number, then we reverse the inequality (reversing inequality means > gets converted to < and vice versa, and ≥ gets converted to ≤ and vice versa) (eg 4>3 means -4<-3)
- If we cross multiply a negative quantity in an inequality, then we reverse the inequality (eg 3 > -2 means -3/2 < 1)
- If we cancel the minus sign from both sides of an inequality, then we reverse the inequality. (eg -3 > -4 means 3 < 4)
- As we usually do not know the sign of a variable term like x, (x-2), etc, so we do not cross-multiply them, as we cannot decide if we have to reverse the sign of inequality or not.
We get a range of solutions while solving inequality which satisfies the inequality,
for e.g. a > 3 gives us a range of solutions, means a ? (3, ∞)
Graphically inequalities can be shown as a region belonging to one side of the line or between lines, for example, inequality -3< x ≤ 5 can be represented as below, a region belonging to -3 and 5 are the region of possible x including 5 and excluding -3.

Inequality Symbols
The most familiar inequality sign is the “not equal sign (≠)”. But to compare the values on the inequalities, the following symbols are used.
Strict Inequality
The strict inequality symbols are (<) and greater than symbol (>). These two symbols are called strict inequalities, as it shows the numbers are strictly greater than or less than each other.
For example,
- 5 < 9 ( 5 is strictly less than 9)
- 10 > 7 (10 is strictly greater than 7)
Slack Inequality
The slack inequalities are less than or equal to symbol (≤) and greater than or equal to symbol (≥). The slack inequalities represent the relation between two inequalities that are not strict.
For example,
- x ≥ 15 ( x is greater than or equal to 15)
- x ≤ 9 (x is less than or equal to 9)
Operation Applied While Solving Inequalities | Sign change? |
|---|---|
| Addition on both sides | No |
| Subtraction on both sides | No |
| Multiplying or dividing both sides by a positive number | No |
| Multiplication or dividing both sides by a negative number | Yes |
| Swapping both sides | Yes |
| Simplify one side | No |
Frequently Used Inequalities
1. $(x-a)(x-b)<0 \Rightarrow x \in(a, b)$, where $a<b$
2. $(x-a)(x-b)>0 \Rightarrow x \in(-\infty, a) \cup(b, \infty)$, where $a<b$
3. $x^2 \leq a^2 \Rightarrow x \in[-a, a]$
4. $x^2 \geq a^2 \Rightarrow x \in(-\infty,-a] \cup[a, \infty)$
How to solve inequalities?
To solve inequalities, follow these steps:
- Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
- Divide by the coefficient of the variable to isolate the variable.
- Write your solution using the inequality symbol.
- Graph the solution set on number line
Graphing Inequalities
While graphing inequalities, we have to keep the following things in mind.
- If the endpoint is included (i.e., in case of ≤ or ≥) use a closed circle.
- If the endpoint is NOT included (i.e., in case of < or >), use an open circle.
- Use open circle at either ∞ or -∞.
- Draw a line from the endpoint that extends to the right side if the variable is greater than the number.
- Draw a line from the endpoint that extends to the left side if the variable is lesser than the number.
Writing Inequalities in Interval Notation
While writing the solution of an inequality in the interval notation, we have to keep the following things in mind.
- If the endpoint is included (i.e., in case of ≤ or ≥) use the closed brackets '[' or ']'
- If the endpoint is not included (i.e., in case of < or >), use the open brackets '(' or ')'
- Use always open bracket at either ∞ or -∞.
Here are some examples to understand the same:
Inequality | Interval |
|---|---|
| x < 2 | (-∞, 2) |
| x > 2 | (2, ∞) |
| x ≤ 2 | (-∞, 2] |
| x ≥ 2 | [2, ∞) |
| 2 < x ≤ 6 | (2, 6] |
Solving Polynomial Inequalities
The polynomial inequalities are inequalities that can be expressed as a polynomial on one side and 0 on the other side of the inequality. There are different types of polynomial inequalities but the important ones are:
- Linear Inequalities
- Quadratic Inequalities
Solving Linear Inequalities
A linear inequality is an inequality that can be expressed with a linear expression on one side and a 0 on the other side. Solving linear inequalities is as same as solving linear equations but just the rules of solving inequalities (that was explained before) should be taken care of.
Solving One Step Inequalities
Consider an inequality 2x < 6 (which is a linear variable is one). To solve this, just one step is sufficient which is dividing both sides by 2. Then we get x < 3. Therefore, the solution of the inequality is x < 3 (or) (-∞, 3).
Solving Two Step Inequalities
Consider an inequality -2x + 3 > 6. To solve this, we need 2 steps. The first step is subtracting 3 from both sides, which gives -2x > 3. Then we need to divide both sides by -2 and it results in x < -3/2 (note that we have changed the sign of the inequality). So the solution of the inequality is x < -3/2 (or) (-∞, -3/2).
Solving Compound Inequalities
These refer to the set of inequalities with either "and" or "or" in between them. For solving inequalities, in this case, just solve each inequality independently and then find the final solution according to the following rules:
- The final solution is the intersection of the solutions of the independent inequalities if we have "and" between them.
- The final solution is the union of the solutions of the independent inequalities if we have "or" between them.
Solving Quadratic Inequalities
A quadratic inequality involves a quadratic in it. Here is the process of solving quadratic inequalities. The process is explained with an example where we are going to solve the inequality x2 - 4x - 5 ≥ 0.
- Step 1: Write the inequality as equation.
x2 - 4x - 5 = 0 - Step 2: Solve the equation.
Then (x - 5) (x + 1) = 0
x = 5; x = -1. - Step 3: Represent the solutions from Step 2 on the number line and identify the intervals. Take care of open circles and closed circles.
Since we have '≥' here (that involves '='), we use closed circles at both 5 and -1. - Step 4: Take a random number from each interval and check whether the inequality is true for that number.
Interval | Random Number | Checking the Inequality |
|---|---|---|
| (-∞, -1] | x = -2 | (-2)2 - 4(-2) - 5 ≥ 0 7 ≥ 0, true |
| [-1, 5] | x = 0 | (0)2 - 4(0) - 5 ≥ 0 -5 ≥ 0, false |
| [5, ∞) | x = 6 | (6)2 - 4(6) - 5 ≥ 0 7 ≥ 0, true |
- Step 5: The inequalities with "true" from the above table are solutions.
Therefore, the solutions of the quadratic inequality x2 - 4x - 5 ≥ 0 is (-∞, -1] U [5, ∞).
We can use the same process for solving cubic inequalities, biquadratic inequalities, etc.
Solving Absolute Value Inequalities
An absolute value inequality includes an algebraic expression inside the absolute value sign. Here is the process of solving absolute value inequalities where the process is explained with an example of solving an absolute value inequality |x + 3| ≤ 2.
- Step 1: Consider the absolute value inequality as equation.
|x + 3| = 2 - Step 2: Solve the equation.
x + 3 = ±2
x + 3 = 2; x + 3 = -2
x = -1; x = -5 - Step 3: Represent the numbers from Step 2 on the number line and identify the intervals.
Since '≤' involves "=", we use closed brackets at -1 and -5. - Step 4: Take a random number for testing from each of the above intervals and check whether the given inequality gets satisfied.
Interval | Random Number | Checking the Inequality |
|---|---|---|
| (-∞, -5] | -6 | |-6 + 3| ≤ 2 3 ≤ 2, false |
| [-5, -1] | -3 | |-3 + 3| ≤ 2 0 ≤ 2, true |
| [-1, ∞) | 0 | |0 + 3| ≤ 2 3 ≤ 2, false |
- Step 5: The intervals that satisfied the inequality are the solution intervals.
Therefore, the solution is |x + 3| ≤ 2 is [-5, -1].
Solving Rational Inequalities
Rational inequalities are inequalities that involve (fractions with variables). To solve the rational inequalities (inequalities with fractions), we just use the same procedure as other inequalities but we have to take care of the excluded points. For example, while solving the rational inequality (x + 2) / (x - 2) < 3, we should note that the rational expression (x + 2) / (x - 2) is NOT defined at x = 2 (set the denominator x - 2 = 0 ⇒x = 2). Let us solve this inequality step by step.
- Step 1: Consider the inequality as the equation.
(x + 2) / (x - 2) = 3 - Step 2: Solve the equation.
x + 2 = 3(x - 2)
x + 2 = 3x - 6
2x = 8
x = 4 - Step 3: Represent the number(s) from the above step and the excluding values on the number line. Note that the open circle/closed circle in case of the numbers from the above step depends on the given inequality whereas we always get an open circle at the excluded number as its name suggests.
Since the given inequality has no "=" sign in it, we just get an open circle at 4, and since 2 is the excluded value we get an open circle at it. - Step 4: Let us take some random numbers from each of the above intervals and test the given inequality.
Interval | Random Number | Checking the inequality |
|---|---|---|
| (-∞, 2) | 0 | (0 + 2) / (0 - 2) < 3 -1 < 3, true |
| (2, 4) | 3 | (3 + 2) / (3 - 2) < 3 5 < 3, false |
| (4, ∞) | 5 | (5 + 2) / (5 - 2) < 3 2.3 < 3, true |
- Step 5: The intervals that have come up with "true" in Step 4 are the solutions.
Therefore, the solution of the rational inequality (x + 2) / (x - 2) < 3 is (-∞, 2) U (4, ∞).
Important Notes on Inequalities
Here are the notes about inequalities:
- If we have <= or >= symbol, then we never get any closed interval in the solution.
- We always get open intervals at ∞ or -∞ symbols because they are NOT numbers to include.
- Write open intervals always at excluded values when solving rational inequalities.
- Excluded values should be taken care of only in case of rational inequalities.
Recommended Video Related to Inequalities
Solved Examples Based On the Inequalities
Hence, the answer is the option 1.
Example 1: Consider the two sets: $A=m \in R$ : both the roots of $x^2-(m+1) x+m+4=0$ are real\} and $B=[-3,5]$
Which of the following is not true?
1) $A-B=(-\infty,-3) \cup(5, \infty)$
2) $A \cap B=-3$
3) $B-A=(-3,5)$
4) $A \cup B=R$
Solution:
$\begin{aligned}
& x^2-(m+1) x+m+4=0 \\
& b^2-4 a c \geqslant 0 \\
& \Rightarrow(m+1)^2-4(m+4) \geqslant 0 \\
& \Rightarrow m^2-2 m-15 \geqslant 0 \\
& \Rightarrow(m-5)(m-3) \geqslant 0 \\
& \Rightarrow m \epsilon(-\infty, 3) \cup(5, \infty)
\end{aligned}$
Example 2: Solution of the inequality $(x+1)(x-2)(x+7)<0$ is
1) $x \in(-7,-1) \cup(2, \infty)$
2) $x \in(-7,1) \cup(2, \infty)$
3) $x \in(-\infty,-7) \cup(-1,2)$
4) $x \in(-\infty,-7) \cup(1,2)$
Solution:
we have $(x+1)(x-2)(x+7)<0$
on number line mark $x=-1,2,-7$

When x > 2, all factors, (x + 1), (x - 2) and (x + 7) is positive
Now put positive and negative signs as shown in the figure
Hence answer is $x \in(-\infty,-7) \cup(-1,2)$
Example 3 : Which values of $x$ satisfy the inequality $(x+1)(x-3)<0$ ?
1) $x \in(-1, \infty)$
2) $x \in(-1,3)$
3) $x \in(-3,1)$
4) $x \in(-\infty, 3)$
Solution:
As we have learned in
Frequently Used Inequalities
1. $(x-a)(x-b)<0 \Rightarrow x \in(a, b)$, where $a<b$
2. $(x-a)(x-b)>0 \Rightarrow x \in(-\infty, a) \cup(b, \infty)$, where $a<b$
3. $x^2 \leq a^2 \Rightarrow x \in[-a, a]$
4. $x^2 \geq a^2 \Rightarrow x \in(-\infty,-a] \cup[a, \infty)$
Now,
Given (x + 1)(x - 3) < 0
on number line mark x = -1, 3

from the concept -1 < x < 3
correct option is $x \in(-1,3)$
Example 4: The solution of the inequation $\frac{x}{2}+\frac{3}{4}>\frac{x}{3}-1$ is
1) $\left(-\infty, \frac{21}{2}\right)$
2) $\left(\frac{-21}{2}, \infty\right)$
3) $(-\infty, \infty)$
4) $(2,3)$
Solution:
$\begin{aligned}
& \frac{x}{2}+\frac{3}{4}>\frac{x}{3}-1 \\
\Rightarrow & \frac{x}{2}-\frac{x}{3}>-1-\frac{3}{4} \\
\Rightarrow & \frac{3 x-2 x}{6}>\frac{-4-3}{4} \\
\Rightarrow & \frac{x}{6}>\frac{-7}{4} \\
\Rightarrow & x>-\frac{7}{4} \times 6 \\
\Rightarrow & x>-\frac{21}{2}
\end{aligned}$
Hence, the answer is option (2).
Example 5: Values of x that satisfy $\frac{x-3}{4}+1 \leqslant \frac{2 x-3}{5}$ are.
1) $\left[\frac{17}{3}, \infty\right)$
2) $(-\infty, \infty)$
3) $\left(-\infty, \frac{17}{3}\right]$
4) $\left[-\frac{17}{3}, \frac{17}{3}\right]$
Solution:
$\begin{aligned}
& \frac{x-3}{4}+1 \leqslant \frac{2 x-3}{5} \\
\Rightarrow & \frac{x-3+4}{4} \leq \frac{2 x-3}{5} \\
\Rightarrow & \frac{x+1}{4} \leq \frac{2 x-3}{5} \\
\Rightarrow & 5(x+1) \leq 4(2 x-3) \\
\Rightarrow & 5 x+5 \leq 8 x-12 \\
\Rightarrow & 5+12 \leq 8 x-5 x \\
\Rightarrow & 17 \leq 3 x
\end{aligned}$
$\begin{aligned} & \Rightarrow \frac{17}{3} \leqslant x \\ & \Rightarrow x \in\left[\frac{17}{3}, \infty\right)\end{aligned}$
Hence, the answer is option (1)
Frequently Asked Questions (FAQs)
Inequalities are the relationship between two expressions that are not equal to one another.
Inequalities have a range of values but equations have a specific value that satisfies it.
Linear inequalities, quadratic inequalities, polynomial inequalities, and rational inequalities are some types of inequalities.
$x^2 < 9 \Rightarrow x^2−9<0 \Rightarrow (x−3)(x+3)<0$
$x \in (−3,3)$