Intersection of Set, Properties of Intersection
The intersection of sets is a core concept in set theory that deals with finding common elements shared by two or more sets. This mathematical operation helps in identifying overlapping data, making it highly useful in subjects like mathematics, logic, data analysis, and computer science. By understanding the properties of the intersection of sets, students can solve problems involving common subsets, Venn diagrams, and real-life grouping scenarios with greater accuracy. In this article, we explore the definition, notation, key properties, and practical applications of set intersection with clear examples and explanations. In this article, we will cover in depth the concept of Intersection. It is an important topic under the chapter of Sets, and we will look at definitions, formulas, important properties and some solved examples.
This Story also Contains
- Intersection of sets: Definition
- Cardinality of the Intersection of Sets Formula
- Venn Diagram for Intersection of Sets
- Properties of the Intersection of Sets
- Intersection Vs Union of Sets
- Real-Life Examples of Set Intersection
- Solved Examples Based On the Intersection of Sets
- List of Topics Related to the Intersection of Sets
- NCERT Resources
- Practice Questions on the Intersection of Sets
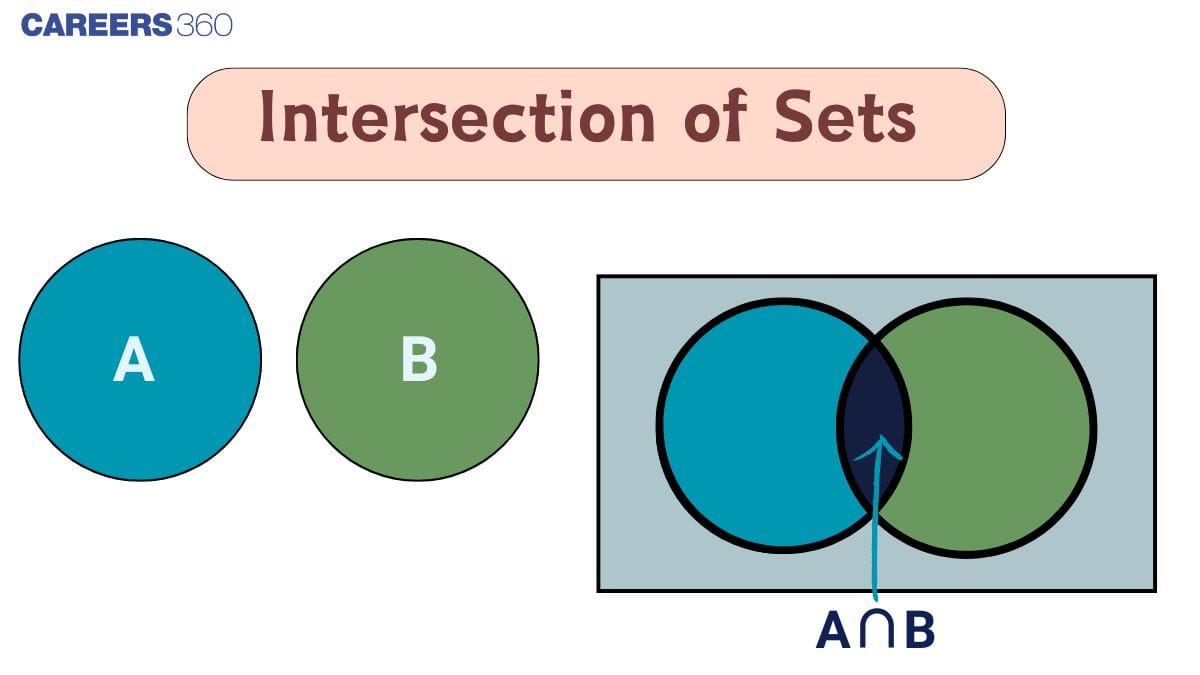
Intersection of sets: Definition
A set is simply a collection of distinct objects, considered as a whole. These objects, called elements or members of the set, can be anything: numbers, people, letters, etc. Intersections of sets represent the common elements in the sets considered.
The intersection of sets $A$ and $B$ is the set of all elements which are common to both $A$ and $B$. The symbol ' $\cap$ ' is used to denote the intersection of sets.
Symbolically, we write $A \cap B=\{x: x \in A$ and $x \in B\}$
If $A$ and $B$ are two sets such that $A \cap B=\varphi$, then $A$ and $B$ are called disjoint sets.
Intersection of Set Notation
The symbol for the intersection of sets is " $\cap$ ". For any two sets $A$ and $B$, the intersection, $A \cap$ $B$ (read as $A$ intersection B) lists all the elements present in both sets (common elements of $A$ and B).
How to Find the Intersection of Sets?
To find the intersection of the set, we can use the following steps:
Step 1: Compare the elements of the given sets.
Step 2: Select the common elements between both sets.
Step 3: Add the selected elements to the resultant set.
Step 4: Repeat above steps for all the given sets.
Step 5: The resultant set obtained represents intersection of sets.
Now let us look into an example of set intersection for better understanding.
Examples of the Intersection of Sets
1. Let $A=\{i,a,f,h,s\}$ and $B=\{f,m,s,h,a,i\}$, then $A \cap B=\{a,s,h,i,f\}$
2. Let $A=\{2,4,6,8\}$ and $B=\{2,3,5,8\}$, then $A \cap B=\{2,8\}$
3. Let $A=\{2,4,6,8\}$ and $B=\{1,3,5,7\}$. Then $A$ and $B$ are disjoint sets because there are no elements that are common to A and B.
4. let $A=\{2,4,6,8\}, B=\{2,3,8\}$, and $C=\{2,3,5,8\}$, then $A \cap B \cap C=\{2,8\}$
Cardinality of the Intersection of Sets Formula
The cardinal number of a set is the total number of elements present in the set. For example, if $\operatorname{Set} A=\{1,2,3,4,5,7,8\}$, then the cardinal number (represented as $\mathrm{n}(\mathrm{A})$ ) $=8$.
Consider two sets $A$ and $B$. Let $A=\{2,4,5,9,10,11,18,21\}, B=\{1,2,3,5,7,8,11,12,13\}$ and $A \cap B=\{2,5,11\}$, and the cardinal number of $A$ intersection $B$ is represented by $n(A \cap B)=3$.
The cardinality of $A \cap B$ can also be found by the formula, $n(A \cap B)=n(A)+$ $n(B)-n(A \cup B)$. Let's verify this formula for the above example, where $n(A)=8, n(B)=9$, and $A \cup B=\{1,2,3,4,5,6,7,8,10,11,12,13,14,21\}$. Note that $n(A \cup B)=14$ here. Then
$ \begin{aligned} & n(A \cap B)=n(A)+n(B)-n(A \cup B) \\ & n(A \cap B)=8+9-14 \\ & n(A \cap B)=3 \end{aligned} $
Venn Diagram for Intersection of Sets
Now, let us look into the Venn diagram of the intersection of sets.
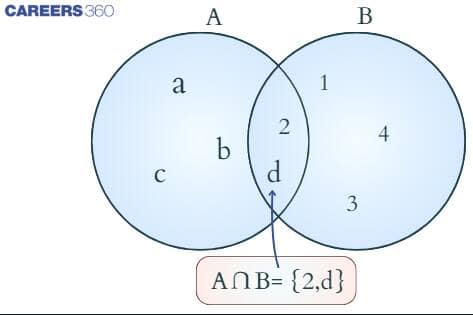
Intersection of two sets
The intersection of two sets signifies that the common element is present in both sets.
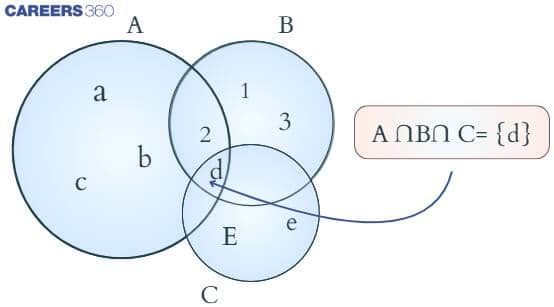
Intersection of three sets
The intersection of three sets signifies that the common element is present in all three sets.
Properties of the Intersection of Sets
This section explains the key algebraic and logical properties that govern the intersection operation in set theory. Understanding these properties of the intersection of sets is essential for solving problems in mathematics, computer science, and data analysis. These rules help simplify complex expressions, especially when working with Venn diagrams, set identities, and Boolean algebra.
Commutative Property of Intersection
The commutative law of intersection states that the order in which two sets are intersected does not affect the result. That is:
$A \cap B = B \cap A$
This means the set of common elements remains the same regardless of the order. For example, if $A = \{1, 2, 3\}$ and $B = \{2, 3, 4\}$, then:
$A \cap B = \{2, 3\} = B \cap A$
This property is useful when rearranging set expressions for simplification.
Associative Property of Intersection
The associative property allows you to group sets in any order when performing multiple intersections:
$(A \cap B) \cap C = A \cap (B \cap C)$
This rule helps in solving complex problems where three or more sets are involved. For instance, with $A = \{1, 2\}$, $B = \{2, 3\}$, and $C = \{2, 4\}$, the intersection will always result in:
$A \cap B \cap C = \{2\}$
irrespective of how the sets are grouped.
Idempotent Property of Intersection
The idempotent law states that intersecting a set with itself returns the same set:
$A \cap A = A$
This shows that intersection is a stabilising operation; applying it repeatedly doesn't change the result. It's a fundamental property used in algebraic proofs and simplifying expressions in set theory and logic.
Identity and Domination Laws in Intersection
These two laws describe how intersection behaves with the universal set and the empty set:
- Identity Law: $A \cap U = A$
where $U$ is the universal set. Intersecting a set with the universal set leaves it unchanged. - Domination Law: $A \cap \emptyset = \emptyset$
where $\emptyset$ is the empty set. No elements are common between any set and the empty set, so the result is always empty.
These properties help in defining the boundaries of sets in both pure mathematics and real-world logic systems.
Distributive Laws Involving Union and Intersection
The distributive property connects the operations of union and intersection:
- Intersection distributes over union:
$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ - Union distributes over the intersection:
$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
These identities are crucial for simplifying complex set expressions, especially in topics like Boolean algebra, database querying, and logic gates.
Intersection with Empty Set and Universal Set
The behaviour of the intersection operation with these two special sets is:
- With an empty set:
$A \cap \emptyset = \emptyset$ - With universal set: $A \cap U = A$
This gives the idea that the universal set acts as a neutral element, while the empty set acts as an absorbing element in set intersection.
Intersection Vs Union of Sets
|
Intersection of Sets
|
Union of Sets
|
|
The intersection of sets contains the common elements in the sets considered.
|
Union of sets contains all the elements in the sets considered.
|
|
The symbol of the intersection of sets is $\cap$.
|
The symbol of the union of sets is $\cup$.
|
|
The formula of cardinality of intersection of sets is $A \cap B = n(A)+n(B)-n(A \cup B)$
|
The formula of cardinality of the union of sets is $A \cup B = n(A)+n(B)-n(A \cap B)$.
|
|
Example: Let $A=\{1,2,3,4,5\}$ and $B = \{4,5,6,7,8\}$. Then, $A \cap B = \{4,5\}$
|
Example: Let $A=\{1,2,3,4,5\}$ and $B = \{4,5,6,7,8\}$. Then, $A \cup B = \{1,2,3,4,5,6,7,8\}$
|
Real-Life Examples of Set Intersection
Some real-life examples of the intersection of sets are
- Consider two gardens $A$ and $B$. The first garden has the set of flowers $\{rose, tulip, sunflower, jasmine\}$. The second garden has the set of flowers $\{ lily, lotus, rose, tulip, daisy\}$. The intersection of sets of flowers in the gardens $A$ and $B$ is $\{rose, tulip\}$.
- Let us consider two genres of books in the library. Let $A$ be the set of books of the science fiction genre and $B$ be the set of books of the mystery genre. The intersection of $A$ and $B$ is the set of science fiction mystery books.
- Let $A$ be the set of all students who play football and $B$ be the set of all students who play cricket. Then the intersection of sets $A$ and $B$ is the set of all students who play both football and cricket.
Solved Examples Based On the Intersection of Sets
Example 1: If $A \cup B=P, A \cap B=Q, B \cap A=R$ and $B \cup A=S$, then which of the following is true?
1) $P=R$
2) $Q=R$
3) $Q=S$
4) $P=Q$
Solution:
According to the property,
$A \cap B=B \cap A$
$\mathrm{Q}=\mathrm{R}$.
Hence, the answer is option 2.
Example 2: Which of the following is the associative property of intersection?
1) $(A \cup B) \cup C=A \cup(B \cup C)$
2) $(A \cap B) \cup C=A \cup(B \cap C)$
3) $A \cap(B \cup C)=(A \cap B) \cup C$
4) $(A \cap B) \cap C=A \cap(B \cap C)$
Solution:
The Associative Property of an intersection is:
$A \cap(B \cap C)=(A \cap B) \cap C$
Hence, the answer is option 4.
Example 3: If $A=\phi$ and $A \cap B=C$, then which of the following is true?
1) $A=B$
2) $A=C$
3) $B=C$
4) $\mathrm{B}=\phi$
Solution:
As we have learned that $\varphi \cap \mathrm{A}=\varphi$
So, $C=A \cap B=\phi \cap B=\phi$
Thus $\mathrm{A}=\mathrm{C}$.
Hence, the answer is option 2.
Example 4: If $A$ and $B$ are equal sets, then which of the following is NOT true?
1) $A \cap B=A$
2) $A \cap B=B$
3) $A \cup B=A \cap B$
4) $A \cap B=\phi$
Solution:
$A \cap B=A \cap A=A$ : so option (1) is true
As $A=B$, so $A \cap B=A=B$ : so option (2) is true
Also, $A \cup B=A \cup A=A$
As $A \cap B=A$, so $A \cup B=A \cap B$: so option (3) is true.
Therefore, the incorrect option is 4.
Hence, the answer is option 4.
Example 5: Given $A \cap B=\{5,7,9\}, A \cap C=\{3,8,7\}$. Find the value of $A \cap(B \cup C)$
1) $\{7\}$
2) $\{3,8,7\}$
3) $\{3,5,7,8,9\}$
4) $\{5,7,9\}$
Solution:
$ \begin{aligned} & A \cap(B \cup C)=(A \cap B) \cup(A \cap C) \quad \text { [Using Distributive Property] } \\ & =\{5,7,9\} \cup\{3,8,7\} \\ & =\{3,5,7,8,9\} \end{aligned} $
Hence, the answer is option 3.
List of Topics Related to the Intersection of Sets
To understand the concept of the intersection of sets thoroughly, it’s important to explore related foundational topics in set theory. Concepts like roster and set builder forms, power sets, complements, and De Morgan's Laws provide the necessary background to master set operations. These interconnected topics not only support a deeper understanding of intersections but also strengthen problem-solving skills in mathematics and logic. In this section, you’ll find a list of key topics that are essential for grasping the intersection of sets and its properties.
NCERT Resources
Mastering the chapter on Sets in Class 11 Mathematics requires the right study materials. NCERT resources such as detailed solutions, concise revision notes, and exam-oriented exemplar problems help strengthen conceptual understanding and problem-solving skills. Whether you're preparing for school exams or competitive tests, these materials provide complete support for systematic learning. In this section, explore the most useful NCERT resources for Chapter 1: Sets.
NCERT Solutions for Class 11 Chapter 1 Sets
Practice Questions on the Intersection of Sets
Mastering any mathematical concept comes through continuous practice. To help strengthen your understanding of the topic, we have given below some practice questions on the Intersection of sets in mathematics. They will test your knowledge of formulas, important properties and general application of knowledge.
To practice questions based on the Intersection of Set - Practice Questions, click here.
You can practice the next topics of Sets below:
Frequently Asked Questions (FAQs)
Let $A$ and $B$ be any two sets. The union of sets $A$ and $B$ is the set that combines the elements in both sets without duplication. The union of sets is denoted by '$\cup$ '. Eg. Let $A=\{s,d,t,g,q,w\}$ and $B=\{g,h,s,t,w,o\}$. Then, $A \cup B = \{s,d,t,g,q,w,h,o\}$.
The intersection of sets $A$ and $B$ is the set of all elements which are common to both $A$ and $B$. The symbol ' $\cap$ ' is used to denote the intersection of sets. Eg. Let $A=\{s,d,t,g,q,w\}$ and $B=\{g,h,s,t,w,o\}$. Then, $A \cap B = \{s,t,g,w\}$.
The symbol $\cap$ represents the combined sets, in other words, the intersecting elements of the mentioned sets. For Example; in case where two sets $X$ and $Y$ are involved then; union of the set $=X \cup Y$ while intersection of the set $=X \cap Y$
The formula of cardinality of intersection of sets is $A \cap B = n(A)+n(B)-n(A \cup B)$
The other symbol for intersection is 'AND'.
However, it goes without saying that $A \cap B=B \cap A$ which is a general property of an intersection operation - that is a commutative prodigy.