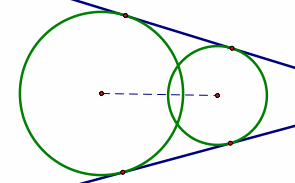
Intersection of Two Circle

An intersection of the circle is one of the most fundamental concepts in mathematics. Geometric shapes consist of all points in a plane equidistant from a fixed point called the centre of a circle. It is a fundamental shape that is constantly used in mathematics. The circle's main applications are geometry, engineering for designing circular instruments, physics, and technology.

Intersection of Two Circle

A circle is the locus of a moving point such that its distance from a fixed point is constant.

The fixed point is called the centre (O) of the circle and the constant distance is called its radius (r)

There are different cases of the intersection of two circles:

Let the two circles be $\left(x-x_1\right)^2+\left(y-y_1\right)^2=r_1^2$ and $\left(x-x_2\right)^2+\left(y-y_2\right)^2=r_2^2$ where centres are $C_1\left(x_1, y_1\right)$ and $C_2\left(x_2, y_2\right)$ and radii are $r_1$ and $r_2$, respectively.

CASE 1
When two circles do not intersect

$
\mathrm{C}_1 \mathrm{C}_2>\mathrm{r}_1+\mathrm{r}_2
$

i.e., the distance between the centres is greater than the sum of radii, then two circles neither intersect nor touch each other.

In this case, four common tangents can be drawn to two circles, in which two are direct common tangents and the other two are transverse common tangents.

Here, point D divides C₁ and C₂ internally in the ratio r₁:r₂ and point P divides C₁ and C₂ externally in the ratio r₁:r₂

Then the co-ordinates of $P$ and $D$ are

$
\begin{aligned}
& D \equiv\left(\frac{r_1 x_2+r_2 x_1}{r_1+r_2}, \frac{r_1 y_2+r_2 y_1}{r_1+r_2}\right)=(\alpha, \beta) \\
& P \equiv\left(\frac{r_1 x_2-r_2 x_1}{r_1-r_2}, \frac{r_1 y_2-r_2 y_1}{r_1-r_2}\right)=(\gamma, \delta)
\end{aligned}
$
The transverse common tangents will pass through the point $D(\alpha, \beta)$. The equation of transverse common tangents is $(y-\beta)=m_1(x-\alpha)$
The direct common tangents will pass through the point $P(V, \delta)$ so the equation of tangents will be $(y-\delta)=m_2(x-V)$.

Now values of m₁ and m₂ can be obtained from the length of the perpendicular from the centre C₁ or C₂ on the tangent is equal to r₁ or r₂. Put two values of m₁ and m₂ on the common tangent equations, then we get the required results.

CASE 2

When two circles touch each other externally

$C_1 C_2=r_1+r_2$

i.e, the distance between the centres is equal to the sum of radii, then two circles touch externally.

In this case, two direct common tangents are real and distinct while the transverse tangents are coincident.

Direct common tangent can be found as done in case 1

For Transverse common tangent
The equation of tangent at point P is $S_1-S_2=0$, where $S_1=0$ and $S_2=0$ are equations of the circles

CASE 3

When two circles intersect at 2 distinct points

$\left|\mathrm{r}_1-\mathrm{r}_2\right|<\mathrm{C}_1 \mathrm{C}_2<\mathrm{r}_1+\mathrm{r}_2$

Thus two common tangents can be drawn

Direct common tangent can be found as done in case 1

CASE 4

When two circles touch each other internally
$
\mathrm{C}_1 \mathrm{C}_2=\left|\mathrm{r}_1-\mathrm{r}_2\right|
$
Thus, only one tangent can be drawn. The equation of the common transverse tangent is

$
S_1-S_2=0
$

CASE-5

When one circle lies inside the other one

$\mathrm{C}_1 \mathrm{C}_2<\left|\mathrm{r}_1-\mathrm{r}_2\right|$

Thus, no common tangent can be drawn.

Recommended Video Based on Intersection of Two Circles

Solved Examples Based on Intersection of Two Circles

Example 1: For the two circles $x^2+y^2=16$ and $x^2+y^2-2 y=0$, there is/are :

1) one pair of common tangents
2) two pairs of common tangents
3) three common tangents
4) no common tangent

Solution

As we learnt in

Common tangents of two circles -

Where two circles neither intersect nor touch each other, there are 4 common tangents.Two are transverse and two are direct common tangents.

- wherein

$\begin{aligned} & S_1: x^2+y^2=16 \\ & r_1=4, C_1:(0,0) \\ & S_2: x^2+y^2-2 y=0 \\ & r_2=1, C_1:(0,1) \\ & C_1 C_2=1 \text { and } r_1-r_2=3\end{aligned}$

There will be no tangent.

Example 2: The centres of a set of circles, each of radius 3, lie on the circle $x^2+y^2=25$. The locus of any point in the set is

$
\begin{aligned}
& \text { 1) } 4 \leq x^2+y^2 \leq 64 \\
& \text { 2) } x^2+y^2 \leq 25 \\
& \text { 3) } x^2+y^2 \geq 25 \\
& \text { 4) } 3 \leq x^2+y^2 \leq 9
\end{aligned}
$

Solution

We should have

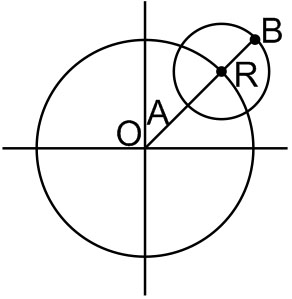
$O A \leqslant O P \leqslant O B$
So, $(5-3) \leqslant \sqrt{x^2+y^2} \leqslant 5+3$

$
4 \leqslant x^2+y^2 \leqslant 64
$
Example 3: If the two circles $(x-1)^2+(y-3)^2=r^2$ and $x^2+y^2-8 x+2 y+8=0$ intersect in two distinct points, then
1) $r<2$
2) $r=2$
3) $r>2$
4) $2<r<8$

Solution

$
\begin{aligned}
& (x-1)^2+(y-3)^2=r^2 \\
& x^2+y^2-8 x+2 y+8=0
\end{aligned}
$

$
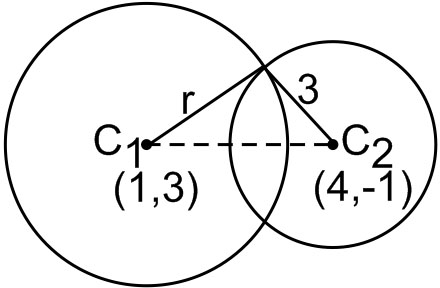
\begin{aligned}
& C_1 C_2=\sqrt{3^2+4^2}=5 \\
& r_1+r_2>5 \\
& r+3>5 \Rightarrow r>2
\end{aligned}
$
Also r-3<5

$
r<8
$
Thus $2<\mathrm{r}<8 \mid$
1) 8
2) 4
3) 9
4) 6

Solution
General form of a circle -

$
x^2+y^2+2 g x+2 f y+c=0
$
$
\begin{aligned}
& \text { centre }=(-g,-f) \\
& \text { radius }=\sqrt{g^2+f^2-c}
\end{aligned}
$
Common tangents of two circle -
When they intersect, there are two common tangents, both of them being direct.

$
\left|r_1-r_2\right|<\left|C_1 C_2\right|<r_1+r_2
$

- wherein

Equation of circle with centre $C_1(1,1)$

$
(x-1)^2+(y-1)^2=4
$
Equation of circle with centre $C_2(3,3)$

$
(x-3)^2+(y-3)^2=4
$
Two circles are orthogonal,
Hence, $
\text { Area }=2\left(\frac{1}{2} \cdot 2 \cdot 2\right)=4 \text { sq.units }
$
Example 5: If the circles $x^2+y^2-16 x-20 y+164=r^2$ and $(x-4)^2+(y-7)^2=36$ intersect at two distinct points, then:
1) $1<r<11$
2) $r=11$
3) $r>11$
4) $0<r<1$

Solution

Common tangents of two circle -

When they intersect, there are two common tangents, both of them being direct.

$\left|r_1-r_2\right|<\left|C_1 C_2\right|<r_1+r_2$

- wherein

From the concept

centre of the circle (-g,-f)

A = (8,10)

and R₁ = r

Similarly,

B = (4,7), R₂ = 6

|R₁ - R₂| < AB < R₁ + R₂

1 < r < 11