Inverse Matrix

A matrix (plural: matrices) is a rectangular arrangement of symbols along rows and columns that might be real or complex numbers. Thus, a system of m x n symbols arranged in a rectangular formation along m rows and n columns is called an m by n matrix (which is written as m x n matrix). The linear system of equations can be solved by using the inverse of the matrix. Environmental science models real-world issues using linear systems as well.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. The inverse of a Matrix
2. Formula to Calculate Inverse of a Matrix A-1
3. Methods to find the inverse of the matrix
4. Summary
5. Solved Examples Based on the Inverse of a Matrix

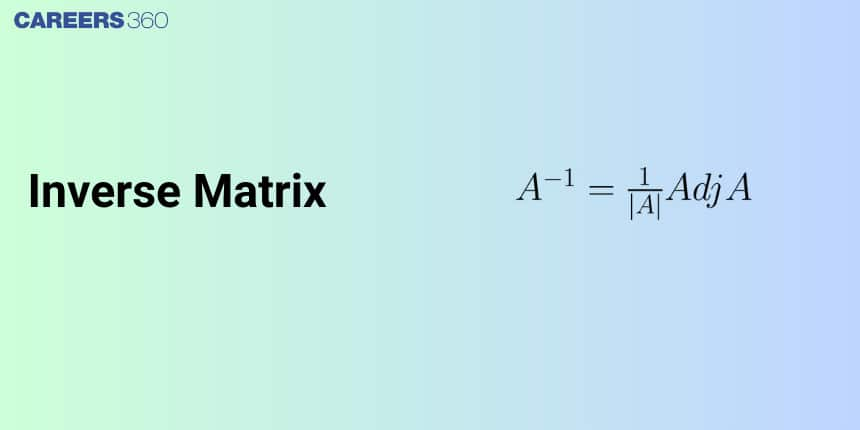
In this article, we will cover the concept of the inverse of matrices. This category falls under the broader category of Matrices, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main Exam (from 2013 to 2023), a total of 16 questions have been asked on this concept, including one in 2014, one in 2016, one in 2017, one in 2018, one in 2019, three in 2020, four in 2021, two in 2022, and two in 2023.

The inverse of a Matrix

A non-singular square matrix A is said to be invertible if there exists a non-singular square matrix B such that

AB = I = BA

and the matrix B is called the inverse of matrix A. Clearly, B should also have the same order as A.

Hence, $\mathrm{A}^{-1}=\mathrm{B} \Leftrightarrow \mathrm{AB}=\mathbb{I}_{\mathrm{n}}=\mathrm{BA}$

Formula to Calculate Inverse of a Matrix A^-1

We know

$
\mathrm{A}(\operatorname{adj} \mathrm{A})=|\mathrm{A}| \mathbb{I}_{\mathrm{n}}
$

Multiplying both sides by $\mathrm{A}^{-1}$
$
\begin{aligned}
& \Rightarrow \mathrm{A}^{-1} \mathrm{~A}(\operatorname{adj} \mathrm{A})=\mathrm{A}^{-1} \mathbb{I}_{\mathrm{n}}|\mathrm{A}| \\
& \Rightarrow \mathbb{I}_{\mathrm{n}}(\operatorname{adjA})=\mathrm{A}^{-1}|\mathrm{~A}| \mathbb{I}_{\mathrm{n}} \quad\left(\text { As } A^{-1} \cdot A=I\right) \\
& \mathrm{A}^{-1}=\frac{\operatorname{adj} \mathrm{A}}{|\mathrm{A}|}
\end{aligned}
$

The inverse of a 2 x 2 Matrix

Let $\mathrm{A}$ is a square matrix of order 2
$
\mathrm{A}=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]
$

Then,
$
\mathrm{A}^{-1}=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]^{-1}=\frac{1}{\mathrm{ad}-\mathrm{bc}}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]
$

The inverse of a 3 x 3 Matrix

To compute the inverse of matrix A of order 3, first check whether the matrix is singular or non-singular.

If the matrix is singular, then its inverse does not exist.

If the matrix is non-singular, then the following are the steps to find the Inverse

We use the formula $A^{-1}=\frac{1}{|A|} \cdot \operatorname{adj}(A)$

1. Calculate the Matrix of Minors,
2. then turn that into the Matrix of Cofactors,
3. then take the transpose (These 3 steps give us the adjoint of matrix A)
4. multiply that by 1/|A|.

Methods to find the inverse of the matrix

Method 1: Directly apply the formula

We use the formula $A^{-1}=\frac{1}{|A|} \cdot \operatorname{adj}(A)$

For example,

Let's compute the inverse of matrix $A$,
$
A=\left[\begin{array}{lll}
1 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]
$

First, find the determinant of $\mathrm{A}$
$
\begin{aligned}
& |\mathrm{A}|=\left|\begin{array}{lll}
1 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right|=1 \cdot(2 \times 1-3 \times 1)-1 \cdot(1 \times 1-3 \times 3)+2 \cdot(1 \times 1-3 \times 2) \\
& |\mathrm{A}|=-3 \neq 0 \\
& \therefore \mathrm{A}^{-1} \text { exists }
\end{aligned}
$

Now, find the minor of each element
$
\begin{aligned}
& \mathrm{M}_{11}=\left|\begin{array}{ll}
2 & 3 \\
1 & 1
\end{array}\right|=2 \times 1-3 \times 1=-1 \\
& \mathrm{M}_{12}=\left|\begin{array}{ll}
1 & 3 \\
3 & 1
\end{array}\right|=1 \times 1-3 \times 3=-8 \\
& \mathrm{M}_{13}=\left|\begin{array}{ll}
1 & 2 \\
3 & 1
\end{array}\right|=1 \times 1-2 \times 3=-5
\end{aligned}
$

Here is the calculation for the whole matrix:

Minor matrix

$
M=\left[\begin{array}{ccc}
2 \times 1-3 \times 1 & 1 \times 1-3 \times 3 & 1 \times 1-2 \times 3 \\
1 \times 1-2 \times 1 & 1 \times 1-2 \times 3 & 1 \times 1-3 \times 1 \\
1 \times 3-2 \times 2 & 1 \times 3-2 \times 1 & 1 \times 2-1 \times 1
\end{array}\right]=\left[\begin{array}{ccc}
-1 & -8 & -5 \\
-1 & -5 & -2 \\
-1 & 1 & 1
\end{array}\right]
$

Now Cofactor of the given matrix
We need to change the sign of alternate cells, like this $\left[\begin{array}{lll}+ & - & + \\ - & + & - \\ + & - & +\end{array}\right]$
So, Cofactor matrix C $=\left[\begin{array}{ccc}+(-1) & -(-8) & +(-5) \\ -(-1) & +(-5) & -(-2) \\ +(-1) & -(1) & +(1)\end{array}\right]=\left[\begin{array}{ccc}-1 & 8 & -5 \\ 1 & -5 & 2 \\ -1 & -1 & 1\end{array}\right]$
Now to find the $\operatorname{adj} \mathrm{A}$, take the transpose of matrix $\mathrm{C}$
Adj $A=C^{\prime}=\left[\begin{array}{ccc}-1 & 1 & -1 \\ 8 & -5 & -1 \\ -5 & 2 & 1\end{array}\right]$
Hence, $A^{-1}=\frac{\operatorname{adj} A}{|A|}$
$A^{-1}=\frac{1}{-3}\left[\begin{array}{ccc}-1 & 1 & -1 \\ 8 & -5 & -1 \\ -5 & 2 & 1\end{array}\right]=\left[\begin{array}{ccc}-\frac{1}{-3} & \frac{1}{-3} & -\frac{1}{-3} \\ \frac{8}{-3} & -\frac{5}{-3} & -\frac{1}{-3} \\ -\frac{5}{-3} & \frac{2}{-3} & \frac{1}{-3}\end{array}\right]$
$
\mathrm{A}^{-1}=\left[\begin{array}{ccc}
\frac{1}{3} & -\frac{1}{3} & \frac{1}{3} \\
-\frac{8}{3} & \frac{5}{3} & \frac{1}{3} \\
\frac{5}{3} & -\frac{2}{3} & -\frac{1}{3}
\end{array}\right]
$

Method 2: Using Elementary Row Transformation

Steps for finding the inverse of a matrix of order 2 by elementary row operations

Step I: Write $A=I_n A$
Step II: Perform a sequence of elementary row operations successively on A on the LHS and the prefactor $I_n$ on the RHS till we obtain the result $I_n=B A$
Step III: Write $A^{-1}=B$

For example:

Given matrix $\mathrm{A}=\left[\begin{array}{cc}a & b \\ c & \left(\frac{1+b c}{a}\right)\end{array}\right]$, then to find the inverse of matrix $\mathrm{A}$
We write,
$
\begin{aligned}
& {\left[\begin{array}{cc}
a & b \\
c & \left(\frac{1+b c}{a}\right)
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right] \mathrm{A}} \\
& \mathrm{R}_1 \rightarrow \frac{1}{\mathrm{a}} \mathrm{R}_1 \\
& {\left[\begin{array}{cc}
1 & \frac{b}{a} \\
c & \left(\frac{1+b c}{a}\right)
\end{array}\right]=\left[\begin{array}{ll}
\frac{1}{a} & 0 \\
0 & 1
\end{array}\right] \mathrm{A}} \\
& \mathrm{R}_2 \rightarrow \mathrm{R}_2-\mathrm{cR}_1 \\
& {\left[\begin{array}{ll}
1 & \frac{b}{a} \\
0 & \frac{1}{a}
\end{array}\right]=\left[\begin{array}{cc}
\frac{1}{a} & 0 \\
\frac{a c}{a} & 1
\end{array}\right] \mathrm{A}} \\
& \mathrm{R}_2 \rightarrow \mathrm{aR} \\
& {\left[\begin{array}{ll}
1 & \frac{b}{a} \\
0 & 1
\end{array}\right]=\left[\begin{array}{cc}
\frac{1}{a} & 0 \\
-c & a
\end{array}\right] \mathrm{A}} \\
& \mathrm{R}_2 \rightarrow \mathrm{R}_1-\frac{\mathrm{b}}{\mathrm{a}} \mathrm{R}_2 \\
& {\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{cc}
\frac{1+b c}{a} & -b \\
-c & a
\end{array}\right] \mathrm{A}} \\
& \mathrm{A}^{-1}=\left[\begin{array}{cc}
\frac{1+b c}{a} & -b \\
-c & a
\end{array}\right]
\end{aligned}
$

Finding the inverse of a Nonsingular 3 x 3 Matrix by Elementary Row Transformations

1. Introduce unity at the intersection of the first row and first column either by interchanging two rows or by adding a constant multiple of elements of some other row to the first row.
2. After introducing unity at (1,1) place introduce zeros at all other places in the first column.
3. Introduce unity at the intersection of the 2nd row and 2nd column with the help of the 2nd and 3rd row.
4. Introduce zeros at all other places in the second column except at the intersection of 2nd row and 2nd column.
5. Introduce unity at the intersection of 3rd row and third column.
6. Finally, introduce zeros at all other places in the third column except at the intersection of third row and third column.

For example, to find the inverse of matrix A

$
A=\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 2 \\
3 & 1 & 1
\end{array}\right]
$

First, write $A=I A$
$
\Rightarrow\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 2 \\
3 & 1 & 1
\end{array}\right]=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right] \mathrm{A}
$

Apply, $R_3 \rightarrow R_3-3 R_1$
$
\Rightarrow\left[\begin{array}{ccc}
1 & 2 & 3 \\
0 & 1 & 2 \\
0 & -5 & -8
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
-3 & 0 & 1
\end{array}\right] \mathrm{A}
$

Apply, $\mathrm{R}_1 \rightarrow \mathrm{R}_1-2 \mathrm{R}_2$

$
\Rightarrow\left[\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & 2 \\
0 & -5 & -8
\end{array}\right]=\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & 0 \\
-3 & 0 & 1
\end{array}\right] \mathrm{A}
$

Apply, $\mathrm{R}_3 \rightarrow \mathrm{R}_3+5 \mathrm{R}_2$
$
\Rightarrow\left[\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & 2 \\
0 & 0 & 2
\end{array}\right]=\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & 0 \\
-3 & 5 & 1
\end{array}\right] \mathrm{A}
$

Apply, $\mathrm{R}_3 \rightarrow \frac{1}{2} \mathrm{R}_3$
$
\Rightarrow\left[\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & 2 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
1 & -2 & 0 \\
0 & 1 & 0 \\
\frac{-3}{2} & \frac{5}{2} & \frac{1}{2}
\end{array}\right] \mathrm{A}
$

Apply, $\mathrm{R}_1 \rightarrow \mathrm{R}_1+\mathrm{R}_3$
$
\Rightarrow\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 2 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
-\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\
0 & 1 & 0 \\
\frac{-3}{2} & \frac{5}{2} & \frac{1}{2}
\end{array}\right] \mathrm{A}
$

Apply, $\mathrm{R}_2 \rightarrow \mathrm{R}_2-2 \mathrm{R}_3$
$
\Rightarrow\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
-\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\
3 & -4 & -1 \\
\frac{-3}{2} & \frac{5}{2} & \frac{1}{2}
\end{array}\right] \mathrm{A}
$

Hence,
$
\mathrm{A}^{-1}=\left[\begin{array}{ccc}
-\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\
3 & -4 & -1 \\
\frac{-3}{2} & \frac{5}{2} & \frac{1}{2}
\end{array}\right]
$

Properties of the inverse of a matrix:

1. The inverse of a matrix is unique

Proof:

Let A be a square and non-singular matrix and let B and C be two inverses of matrix A

$\begin{aligned} & \mathrm{AB}=\mathrm{BA}=\mathbb{I}_{\mathrm{n}} \text { (since } \mathrm{B} \text { is inverse of } \mathrm{A} \text { ) } \\ & \mathrm{AC}=\mathrm{CA}=\mathbb{I}_{\mathrm{n}} \text { (since } \mathrm{C} \text { is inverse of } \mathrm{A} \text { ) } \\ & \text { now, } \mathrm{AB}=\mathbb{I}_{\mathrm{n}} \\ & \left.\mathrm{C}(\mathrm{AB})=\mathrm{CI}_{\mathrm{n}} \quad \text { [Multiplication by } \mathrm{C}\right] \\ & (\mathrm{CA}) \mathrm{B}=\mathrm{CI}_{\mathrm{n}} \quad \text { [by associativity] } \\ & \mathbb{I}_{\mathrm{n}} \mathrm{B}=\mathrm{C} \mathbb{I}_{\mathrm{n}} \Rightarrow B=C \\ & \end{aligned}$

Hence an invertible matrix has a unique inverse.

2. If A and B are invertible matrices of order n, then AB will also be invertible. and (AB)^-1 = B^-1A^-1.

Proof :

$\mathrm{A}$ and $\mathrm{B}$ are invertible matrices, so $|A| \neq 0$ and $|B| \neq 0$
Hence, $|A||B| \neq 0 \Rightarrow|A B| \neq 0$
now, $(A B)\left(B^{-1} A^{-1}\right)=A\left(B B^{-1}\right) A^{-1}$ [by associative law]
$=A\left(I_n\right) A^{-1}$ $\left[\because \mathrm{BB}^{-1}=\mathrm{I}_{\mathrm{n}}\right]$
$=A A^{-1}=I_n$
also, $\left(B^{-1} A^{-1}\right)(A B)=B^{-1}\left(A^{-1} A\right) B$ [by associative law]
$
\begin{aligned}
& =B^{-1}\left(I_n B\right) \\
& =B^{-1} B=I_n
\end{aligned}
$
Thus, $(A B)\left(B^{-1} A^{-1}\right)=I_n=\left(B^{-1} A^{-1}\right)(A B)$
Hence, $(A B)^{-1}=B^{-1} A^{-1}$

3. If A is an invertible matrix, then

(A')^-1 = (A^-1) '

Proof: As A is an invertible matrix, so |A| ≠ 0 ⇒ |A' | ≠ 0. Hence, A' is also invertible.

Now, $\mathrm{AA}^{-1}=\mathbb{I}_{\mathrm{n}}=\mathrm{A}^{-1} \mathrm{~A}$
Taking transpose of all three sides
$
\begin{aligned}
& \Rightarrow\left(\mathrm{AA}^{-1}\right)^{\prime}=\left(\mathbb{I}_{\mathrm{n}}\right)^{\prime}=\left(\mathrm{A}^{-1} \mathrm{~A}\right)^{\prime} \\
& \Rightarrow\left(\mathrm{A}^{-1}\right)^{\prime} \mathrm{A}^{\prime}=\mathbb{I}=\mathrm{A}^{\prime}\left(\mathrm{A}^{-1}\right)^{\prime} \\
& \left(\mathrm{A}^{\prime}\right)^{-1}=\left(\mathrm{A}^{-1}\right)^{\prime}
\end{aligned}
$

4. Let A be an invertible matrix, then, (A^-1)^-1=A

Proof:

Let A be an invertible matrix of order n.

$\begin{aligned} & \text { As } \quad A \cdot A^{-1}=I=A^{-1} \cdot A \\ & \Rightarrow \quad\left(\mathrm{A}^{-1}\right)^{-1}=\mathrm{A}\end{aligned}$

5. Let A be an invertible matrix of order n and k is a natural number, then (A^k)^-1 = (A^-1)^k = A^-k

Proof:

$\begin{aligned}\left(\mathrm{A}^{\mathrm{k}}\right)^{-1} & =(\mathrm{A} \times \mathrm{A} \times \mathrm{A} \times \ldots \times \mathrm{A})^{-1} \\ & =\left(\mathrm{A}^{-1} \times \mathrm{A}^{-1} \times \mathrm{A}^{-1} \times \ldots \times \mathrm{A}^{-1}\right) \\ & =\left(\mathrm{A}^{-1}\right)^k\end{aligned}$

6. Let A be an invertible matrix of order n, then

$
\left|\mathrm{A}^{-1}\right|=\frac{1}{|\mathrm{~A}|}
$

Proof: $\because A$ is invertible, then $|A| \neq 0$.
now, $\mathrm{AA}^{-1}=\mathbb{I}_{\mathrm{n}}=\mathrm{A}^{-1} \mathrm{~A}$
$
\begin{aligned}
& \Rightarrow\left|\mathrm{AA}^{-1}\right|=\left|\mathbb{I}_{\mathrm{n}}\right| \\
& \Rightarrow|\mathrm{A}|\left|\mathrm{A}^{-1}\right|=1 \\
& \Rightarrow\left|\mathrm{A}^{-1}\right|=\frac{1}{|\mathrm{~A}|}
\end{aligned}
$

7. The inverse of a non-singular diagonal matrix is a diagonal matrix

if $A=\left[\begin{array}{lll}a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c\end{array}\right]$ and $|\mathrm{A}| \neq 0$
then
$
\mathrm{A}^{-1}=\left[\begin{array}{ccc}
\frac{1}{a} & 0 & 0 \\
0 & \frac{1}{b} & 0 \\
0 & 0 & \frac{1}{c}
\end{array}\right]
$

Summary

The inverse of a matrix is a fundamental concept in linear algebra. It plays a crucial role in various mathematical and real-world applications. Knowing the inverse of the matrix helps us to solve the system of equations by various methods. The inverse of the matrix also helps us to solve equations by Gauss elimination method.

Recommended Video :

Solved Examples Based on the Inverse of a Matrix

Example 1: The set of all values of $t \in \mathbb{R}$, for which the matrix $\left[\begin{array}{ccc}e^t & e^{-t}(\sin t-2 \cos t) & \mathrm{e}^{-t}(-2 \sin t-\cos t) \\ \mathrm{e}^t & \mathrm{e}^{-t}(2 \sin t+\cos t) & e^{-t}(\sin t-2 \cos t) \\ \mathrm{e}^t & e^{-t} \cos t & e^{-t} \sin t\end{array}\right]$ is invertible, is [JEE MAINS 2023]

Solution:

$\begin{aligned} & |\mathrm{A}|=\left|\begin{array}{ccc}\mathrm{e}^t & \mathrm{e}^{-t}(s-2 c) & \mathrm{e}^{-t}(-2 \mathrm{~s}-\mathrm{c}) \\ \mathrm{e}^{\mathrm{t}} & \mathrm{e}^{-t}(2 \mathrm{~s}+\mathrm{c}) & \mathrm{e}^{-t}(\mathrm{~s}-2 \mathrm{c}) \\ \mathrm{e}^{\mathrm{t}} & \mathrm{e}^{-t} \mathrm{c} & \mathrm{e}^{-t} \mathrm{~s}\end{array}\right| \\ & \Rightarrow\mathrm{e}^t \cdot \mathrm{e}^{-t} \cdot \mathrm{e}^{-t}\left|\begin{array}{ccc}1 & \mathrm{~s}-2 \mathrm{c} & -2 \mathrm{~s}-\mathrm{c} \\ 1 & 2 s+c & \mathrm{~s}-2 \mathrm{c} \\ 1 & \mathrm{c} & \mathrm{s}\end{array}\right| \\ & R_1 \rightarrow R_1-R_2 \& \quad R_2 \rightarrow R_2-R_3 \\ & =\mathrm{e}^{\mathrm{t}}\left|\begin{array}{ccc}0 & -\mathrm{s}-3 \mathrm{c} & -3 \mathrm{~s}-\mathrm{c} \\ 0 & 2 \mathrm{~s} & -2 \mathrm{c} \\ 1 & \mathrm{c} & \mathrm{s}\end{array}\right| \\ & \Rightarrow \mathrm{e}^{-\mathrm{t}}\left[1\left(2 \mathrm{sc}+6 \mathrm{c}^2+6 \mathrm{~s}^2+2 \mathrm{sc}\right)\right] \\ & \Rightarrow \mathrm{e}^{-\mathrm{t}}\left[4 \mathrm{sc}+6\left(\mathrm{c}^2+\mathrm{s}^2\right)\right]=\mathrm{e}^{-\mathrm{t}}(6+2 \sin 2 \mathrm{t}) \\ & \because 2 \sin 2 \mathrm{t} \in[-2,2] \\ & \therefore \mathrm{e}^{-\mathrm{t}}(6+2 \sin 2 \mathrm{t}) \neq 0 \quad \forall \mathrm{t} \in \mathrm{R} \\ & \end{aligned}$

Hence the set of all values of t is real numbers(R)

Example 2: Let
$
\mathrm{X}=\left[\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right], \mathrm{Y}=\alpha \mathrm{I}+\beta \mathrm{X}+\gamma \mathrm{X}^2
$ and $\mathrm{Z}=\alpha^2 I-\alpha \beta \mathrm{X}+\left(\beta^2-\alpha \gamma\right) \mathrm{X}^2, \alpha, \beta, \gamma \in \mathbb{R} \text {.If } \mathrm{Y}^{-1}=\left[\begin{array}{ccc}
1 / 5 & -2 / 5 & 1 / 5 \\
0 & 1 / 5 & -2 / 5 \\
0 & 0 & 1 / 5
\end{array}\right] \text {, then } \mathbf{n}:(\alpha-\beta+\gamma)^2 \text { is equal to }$

[JEE MAINS 2022]

Solution:

$
\begin{aligned}
& \mathrm{x}=\left[\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right] \\
& x^2=\left[\begin{array}{lll}
0 & 0 & 1 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right] \\
& \therefore \mathrm{y}=\alpha \mathrm{I}+\beta \mathrm{x}+\gamma \mathrm{x}^2 \\
& \mathrm{y}=\left[\begin{array}{lll}
\alpha & \beta & \gamma \\
0 & \alpha & \beta \\
0 & 0 & \alpha
\end{array}\right]
\end{aligned}
$
$
\mathrm{z}=\left[\begin{array}{ccc}
\alpha^2 & -\alpha \beta & \beta^2-\alpha r \\
0 & \alpha^2 & -\alpha \beta \\
0 & 0 & \alpha^2
\end{array}\right]
$

As $\mathrm{yy}^{-1}=\mathrm{I}$ then
$
\begin{aligned}
& \alpha=5, \quad \beta=10, \gamma=15 \\
& \therefore(\alpha-\beta+\gamma)^2=100
\end{aligned}
$

Hence, the answer is 100.

Example 3: Let $A$ and $B$ be two $3 \times 3$ real matrices such that $\left(A^2-B^2\right)$ is an invertible matrix. If $A^5=B^5$ and $\mathrm{A}^3 \mathrm{~B}^2=\mathrm{A}^2 \mathrm{~B}^3$, then the value of the determinant of the matrix $\mathrm{A}^3+\mathrm{B}^3$ is equal to: [JEEMAINS 2021]

Solution:

$
A^5=B^5 \quad \& \quad A^3 B^2=A^2 B^3
$

Subtracting these
$
\begin{aligned}
& A^5-A^3 B^2=B^5-A^2 B^3 \\
\Rightarrow & A^3\left(A^2-B^2\right)=-B^3\left(A^2-B^2\right) \\
\Rightarrow & \left(A^3+B^3\right)\left(A^2-B^2\right)=0 \\
\Rightarrow & \left|A^3+B^3\right| \cdot\left|A^2-B^2\right|=0 \\
\Rightarrow & \left|A^3+B^3\right|=0\left(\text { As }\left|A^2-B^2\right| \neq 0\right) .
\end{aligned}
$

Hence, $\mathrm{A}^3+\mathrm{B}^3=0$

Example 4: The number of matrices $\mathrm{A}=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$, where $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d} \in\{-1,0,1,2,3, \ldots \ldots, 10\}$, such that $\mathrm{A}=\mathrm{A}^{-1}$, is
[JEE MAINS 2022]

Solution:

$\begin{aligned} & \mathrm{A}=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right] \\ & \mathrm{A}=\mathrm{A}^{-1} \\ & \Rightarrow \mathrm{AA}=\mathrm{A}^{-1} \mathrm{~A} \\ & \Rightarrow \mathrm{A}^2=\mathrm{I} \\ & \Rightarrow\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right] \\ & \Rightarrow\left[\begin{array}{ll}a^2+b c & a b+b d \\ a c+c d & b c+d^2\end{array}\right]=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right] \\ & \therefore \mathrm{a}^2+\mathrm{bc}=1, \mathrm{~d}^2+\mathrm{bc}=1, \mathrm{~b}(\mathrm{a}+\mathrm{d})=0, \mathrm{c}(\mathrm{a}+\mathrm{d})=0\end{aligned}$

From the first two equations,

$
\mathrm{a}^2=\mathrm{d}^2 \Rightarrow \mathrm{a}=\mathrm{d}, \mathrm{a}=-\mathrm{d}
$

Case I: $\mathrm{a}=-\mathrm{d}$
$(\mathrm{a}, \mathrm{d})$ can be $(0,0),(1,-1),(-1,1)$. For these $\mathrm{b}, \mathrm{c}$ can have 2,23 and 23 values $=48$ values
Case II : $\mathrm{a}=\mathrm{d}$
$(\mathrm{a}, \mathrm{d})$ can be $(1,1)_{\text {or }}(-1,-1)$. For this $(\mathrm{b}, \mathrm{c})$ can be $(0,0)$ only
$\therefore$ Total $=48+2=50$

Hence answer is 50

Example 5 :Let $\mathrm{A}=\left[\begin{array}{cc}1 & 2 \\ -1 & 4\end{array}\right]$. If $\mathrm{A}^{-1}=\alpha \mathrm{I}+\beta \mathrm{A}, \alpha, \beta \in \mathbf{R}, \mathrm{I}$ is a $2 \times 2$ identity matrix, then $4(\alpha-\beta)$ is equal to:
[JEE MAINS 2021]

Solution:

$
\begin{aligned}
& \text { Given } A=\left[\begin{array}{rr}
1 & 2 \\
-1 & 4
\end{array}\right] \\
& \begin{aligned}
& \Rightarrow|A|=4+2=6, \text { so inverse exists } \\
& \text { Now } A^{-1}=\frac{\operatorname{adj}(A)}{|A|}=\frac{1}{6}\left[\begin{array}{cc}
4 & -2 \\
1 & 1
\end{array}\right] \\
&=\left[\begin{array}{cc}
\frac{2}{3} & -\frac{1}{3} \\
\frac{1}{6} & \frac{1}{6}
\end{array}\right]
\end{aligned}
\end{aligned}
$

As $A^{-1}=\alpha I+\beta A$

$\begin{aligned} & \Rightarrow\left[\begin{array}{cc}\frac{2}{3} & -\frac{1}{3} \\ \frac{1}{6} & \frac{1}{6}\end{array}\right]=\left[\begin{array}{ll}\alpha & 0 \\ 0 & \alpha\end{array}\right]+\left[\begin{array}{cc}\beta & 2 \beta \\ -\beta & 4 \beta\end{array}\right] \\ & \Rightarrow\left[\begin{array}{cc}\frac{2}{3} & -\frac{1}{3} \\ \frac{1}{6} & \frac{1}{6}\end{array}\right]=\left[\begin{array}{cc}\alpha+\beta & 2 \beta \\ -\beta & \alpha+4 \beta\end{array}\right] \\ & \therefore \quad-\beta=\frac{1}{6} \Rightarrow \beta=-\frac{1}{6} \\ & \Rightarrow \alpha+\beta=\frac{2}{3} \Rightarrow \alpha=\frac{5}{6} \\ & \therefore \quad 4(\alpha-\beta)=4\left(\frac{5}{6}+\frac{1}{6}\right) \\ & =4\end{aligned}$

Hence, the answer is 4.