Lagrange's Identity: Definition, Formula, Proof & Example

Before knowing about Lagrange's Identity let's revise the vector triple product. It is defined as the cross product of one of the vectors with the cross product of the other two vectors. It results in the vector. For threevectors $\vec{a}, \vec{b}$ and $\vec{c}$ vectar triple product is defined as $\vec{a} \times(\vec{b} \times \vec{c})$. In real life, we use vector triple product in cryptography for secure data transmission and aid in network analysis and error correction coding.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Lagrange's Identity
2. Derivation of Lagrange's Identity
3. Properties of Lagrange's Identity
4. Solved Examples Based on Lagrange's Identity

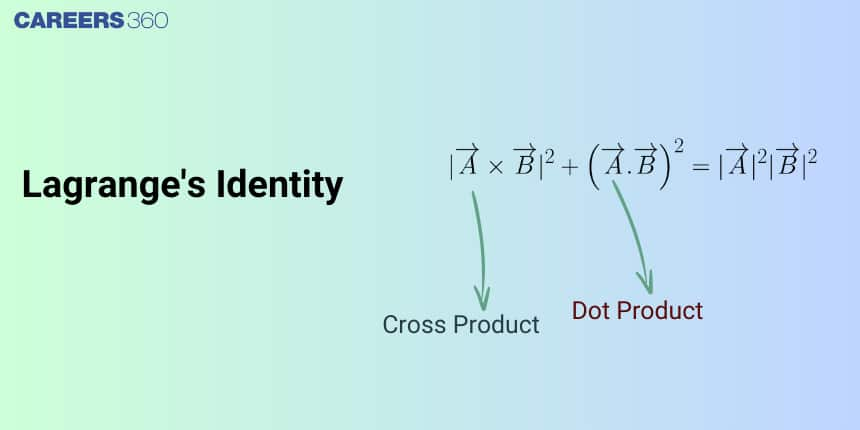
In this article, we will cover the concept of Lagrange's Identity. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of ten questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2022.

Lagrange's Identity

Langrange's Identity is a formula that gives the length of the wedge product of two vectors, which is the area of the parallelogram, in terms of the dot products of the two vectors.

$\begin{aligned}(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d}) & =\left|\begin{array}{ll}\vec{a} \cdot \vec{c} & \vec{a} \cdot \vec{d} \\ \vec{b} \cdot \vec{c} & \vec{b} \cdot \vec{d}\end{array}\right| \\ & =(\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d})-(\vec{a} \cdot \vec{d})(\vec{b} \cdot \vec{c})\end{aligned}$

Derivation of Lagrange's Identity

$\begin{aligned} & \text { Let } \quad(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \cdot(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}})=\overrightarrow{\mathrm{u}} \cdot(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}}) \\ & \text {where } \begin{aligned}(\vec{a} \times \vec{b})) & \\ = & \overrightarrow{\mathrm{u}}=(\overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{c}}) \cdot \overrightarrow{\mathrm{d}} \\ = & ((\overrightarrow{\mathrm{a}} \times \vec{b}) \times \overrightarrow{\mathrm{c}}) \cdot \overrightarrow{\mathrm{d}} \\ & =((\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{b}}-(\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{b}}) \overrightarrow{\mathrm{a}}) \cdot \overrightarrow{\mathrm{d}}\end{aligned}\end{aligned}$

$\begin{aligned} & =(\vec{c} \cdot \vec{a})(\vec{b} \cdot \vec{d})-(\vec{c} \cdot \vec{b})(\vec{a} \cdot \vec{d}) \\ & =(\vec{a} \cdot \vec{c})(\vec{b} \cdot \vec{d})-(\vec{a} \cdot \vec{d})(\vec{b} \cdot \vec{c})\end{aligned}$

NOTE:

$
\begin{aligned}
(\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d}) & =\left[\begin{array}{lll}
(\vec{a} \times \vec{b}) \cdot \vec{d}
\end{array}\right] \vec{c}-[(\vec{a} \times \vec{b}) \cdot \vec{c}] \vec{d} \\
& =\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{d}
\end{array}\right] \vec{c}-\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right] \vec{d}
\end{aligned}
$

$\Rightarrow$ Thus, vector $\overrightarrow{(a} \times \vec{b}) \times(\vec{c} \times \vec{d})$ lies in the plane of $\vec{c}$ and $\vec{d}$

If we take the dot product of two systems of vectors and get unity, then the system is called the reciprocal system of vectors.

Thus if $\tilde{\mathrm{a}}, \tilde{\mathrm{b}}$ and $\tilde{\mathrm{c}}$ are three non - coplanar vectors, and if $\overrightarrow{a^{\prime}}=\frac{\vec{b} \times \vec{c}}{\left[\begin{array}{ll}\vec{a} & \vec{b}\end{array}\right]}$, $\overrightarrow{b^{\prime}}=\frac{\vec{c} \times \vec{a}}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}$ and $\overrightarrow{c^{\prime}}=\frac{\vec{a} \times \vec{b}}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}$ then $\overrightarrow{a^{\prime}}, \overrightarrow{b^{\prime}}, \overrightarrow{c^{\prime}}$ are said to be the reciprocal systems vectors for vectors $\vec{a}, \vec{b}$ and $\vec{c}$.

Properties of Lagrange's Identity

1. If $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ and $\overrightarrow{\mathbf{a}^{\prime}}, \overrightarrow{\mathbf{b}^{\prime}}$ and $\overrightarrow{\mathbf{c}^{\prime}}$are a reciprocal system of vectors, then $\vec{a} \cdot \overrightarrow{a^{\prime}}=\frac{\vec{a} \cdot(\vec{b} \times \vec{c})}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}=\frac{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}{\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]}=1$

Similarly,

$\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{b}^{\prime}}=\overrightarrow{\mathbf{c}} \cdot \overrightarrow{\mathbf{c}^{\prime}}=1$

Due to the above property, the two systems of vectors are called reciprocal systems.

2. $\vec{a} \cdot \overrightarrow{b^{\prime}}=\vec{a} \cdot \overrightarrow{c^{\prime}}=\vec{b} \cdot \overrightarrow{a^{\prime}}=\vec{b} \cdot \overrightarrow{c^{\prime}}=\overrightarrow{c^{\prime}} \cdot \overrightarrow{a^{\prime}}=\overrightarrow{c^{\prime}} \cdot \overrightarrow{b^{\prime}}=0$
3. $\left[\begin{array}{lll}\overrightarrow{\mathrm{a}} & \overrightarrow{\mathrm{b}} & \overrightarrow{\mathrm{c}}\end{array}\right]\left[\begin{array}{lll}\overrightarrow{a^{\prime}} & \overrightarrow{b^{\prime}} & \overrightarrow{c^{\prime}}\end{array}\right]=1$

4. The orthogonal triad of vectors $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ is self-reciprocal.
5. $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ are non-coplanar iff $\overrightarrow{\mathbf{a}}^{\prime}, \overrightarrow{\mathbf{b}^{\prime}}$ and $\overrightarrow{\mathbf{c}^{\prime}}$ are non-coplanar.

As $\left[\begin{array}{lll}\overrightarrow{a^{\prime}} & \overrightarrow{b^{\prime}} & \vec{c}\end{array}\right]\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]=1$ and $\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right] \neq 0$ are non-coplanar

$
\Leftrightarrow \frac{1}{\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]} \neq 0 \Leftrightarrow\left[\begin{array}{lll}
\overrightarrow{a^{\prime}} & \overrightarrow{b^{\prime}} & \overrightarrow{c^{\prime}}
\end{array}\right]
$

are non-coplanar.

Recommended Video Based on Lagrange's Identity

Solved Examples Based on Lagrange's Identity

Fxample 1: Let $\mathrm{a}, \mathrm{b}$ be two vectors such that $|\mathrm{a} . \mathrm{b}|^2=9$ and $|\mathrm{a} \times \mathrm{b}|^2=75$. Then $|\vec{a}|^2$ is equal to - $\qquad$
Solution

$
\begin{aligned}
& |\tilde{\mathrm{a}}+\tilde{\mathrm{b}}|^2=|\tilde{\mathrm{a}}|^2+2|\tilde{\mathrm{b}}|^2 \\
& \Rightarrow|\tilde{\mathrm{a}}|^2+|\tilde{\mathrm{b}}|^2+2 \tilde{\mathrm{a}} \cdot \tilde{\mathrm{b}}^2=|\overrightarrow{\mathrm{a}}|^2+2|\vec{b}|^2 \\
& \Rightarrow|\tilde{\mathrm{b}}|^2=+2|\tilde{\mathrm{a}}| \cdot|\tilde{\mathrm{b}}|^2=6 \\
& \Rightarrow|\tilde{\mathrm{b}}|=\sqrt{6} \\
& |\tilde{\mathrm{a}} \cdot \tilde{\mathrm{b}}|^2+|\tilde{\mathrm{a}} \times \tilde{\mathrm{b}}|^2=|\tilde{\mathrm{a}}|^2|\mathrm{~b}|^2 \\
& \Rightarrow 9+75=|\tilde{\mathrm{a}}|^2 \cdot 6 \\
& \Rightarrow|\tilde{\mathrm{a}}|^2=\frac{84}{6}=14
\end{aligned}
$
Hence, the answer is 14

Example 2: If $\vec{a}$ and $\vec{b}$ are two vectors such that $|\vec{a}|=3$ and $|\vec{b}|=2$ then $|\vec{a} * \vec{b}|^2+(\vec{a} \cdot \vec{b})^2$ equals
Solution: We know that Lagrange's identity -

$
(\vec{a} \times \vec{b})=|\vec{a}|^2|\vec{b}|^2-(\vec{a} \cdot \vec{b})^2
$
Here $\vec{a}$ and $\vec{b}$ are two vectors

$
\begin{aligned}
& |\vec{a} * \vec{b}|^2+(\vec{a} \cdot \vec{b})^2=|\vec{a}|^2|\vec{b}|^2 \sin ^{2 \theta}+|\vec{a}|^2|\vec{b}|^2 \cos ^{2 \Theta} \\
& =|\vec{a}|^2|\vec{b}|^2=9 * 4=36
\end{aligned}
$
Hence, the answer is 36

Example 3: $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ are vectors then $(\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d})$ equals:
Solution

$
\begin{aligned}
& (\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d})=-[(\vec{c} \times \vec{d}) \times(\vec{a} \times \vec{b})]=-[((\vec{c} \times \vec{d}) \cdot \vec{b}) \vec{a}-((\vec{c} \times \vec{d}) \cdot \vec{a}) \vec{b}] \\
& =\left[\begin{array}{lll}
\vec{a} & \vec{c} & \vec{d}
\end{array}\right] \vec{b}-\left[\begin{array}{lll}
\vec{b} & \vec{c} & \vec{d}] \vec{a}
\end{array}\right.
\end{aligned}
$
Hence, the answer is $[\vec{a} \vec{c} \vec{d}] \vec{b}-[\vec{b} \vec{c} \vec{d}] \vec{a}$
Example 4: $\vec{a}$ and $\vec{b}$ are vectors such that $\left|\begin{array}{ll}\vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} \\ \vec{a} \cdot \vec{b} & \vec{b} \cdot \vec{b}\end{array}\right|=16 \quad|\vec{a} \times \vec{b}|_{\text {equals }}$
Solution

$
\begin{aligned}
& \left|\begin{array}{ll}
\vec{a} \cdot \vec{a} & \vec{a} \cdot \vec{b} \\
\vec{a} \cdot \vec{b} & \vec{b} \cdot \vec{b}
\end{array}\right|=16 \Rightarrow|\vec{a}|^2|\vec{b}|^2-(\vec{a} \cdot \vec{b})^2=16 \\
& \Rightarrow|\vec{a} \times \vec{b}|^2=16 \Rightarrow|\vec{a} \times \vec{b}|=4
\end{aligned}
$
Hence, the answer is 4

Example 5: Let $\vec{a}, \vec{b}, \vec{c}$ are three non-coplanar vectors, such that $[\vec{a} \vec{b} \vec{c}]=2$ the reciprocal system of vectors will form a parallelepiped with volume:
Solution: Reciprocal System of Vectors -

$
\begin{aligned}
& \vec{a}^{\prime}=\frac{\vec{b} \times \vec{c}}{[\vec{a} \vec{b} \vec{c}]} \\
& \vec{b}^{\prime}=\frac{\vec{c} \times \vec{a}}{[\vec{a} \vec{b} \vec{c}]} \\
& \vec{c}^{\prime}=\frac{\vec{a} \times \vec{b}}{[\vec{a} \vec{b} \vec{c}]}
\end{aligned}
$

$\vec{a}, \vec{b}, \vec{c}_{\text {are three vectors }}$

$
\text { i.e. } \frac{\vec{b} \times \vec{c}}{2}, \frac{\vec{c} \times \vec{a}}{2}, \frac{\vec{a} \times \vec{b}}{2}
$
$
\begin{aligned}
& \text { the volume of parallelepiped }=\left|\left[\begin{array}{lll}
\frac{\vec{b} \times \vec{c}}{2} \frac{\vec{c} \times \vec{a}}{2} \frac{\vec{a} \times \vec{b}}{2}
\end{array}\right]\right| \\
& \left|\frac{1}{8}\left[\begin{array}{lll}
\vec{b} \times \vec{c} & \vec{c} \times \vec{a} & \vec{a} \times \vec{b}
\end{array}\right]\right|=1 / 8\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]^2 \\
& 1 / 8 \times 4=1 / 2
\end{aligned}
$
Hence, the answer is $1 / 2$

Summary

Lagrange identity is an important concept in vector algebra which describes the relationship between geometric and algebraic identity. Its ability to connect geometric interpretations with algebraic formulations makes it indispensable for understanding vector relationships and solving complex problems involving vectors in space. Understanding Lagrange's identity helps us to analyze and solve complex problems.