Law of Cosines: Proof and Examples

The solution of triangles involves the application of properties, rules, and theorems to analyze them more deeply. Some of these rules are the Sine rule, Cosine rule, Tangent rule, Projection rule, etc. These rules can be applied to analyze triangles involved in different cases. The law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. In real life, we use the Law of cosine in radio waves, tides, musical tones, and electrical currents.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Triangle
2. Law of Cosines: definition
3. Cosine Rule
4. Summary
5. Solved Examples Based on Cosine Rule

In this article, we will cover the concept of the cosine rule. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of eleven questions have been asked on this concept, including three in 2014, two in 2015, two in 2016, two in 2017, one in 2019 and one in 2023.

Triangle

A triangle is a polygon with 3 sides. A triangle is more special as compared to other polygons as it is the polygon having the least number of sides. A triangle has six main elements, three sides, and three angles. There are different rules and theorems for triangles that relate their sides and angles.

A few standard symbols to represent elements of the triangle:

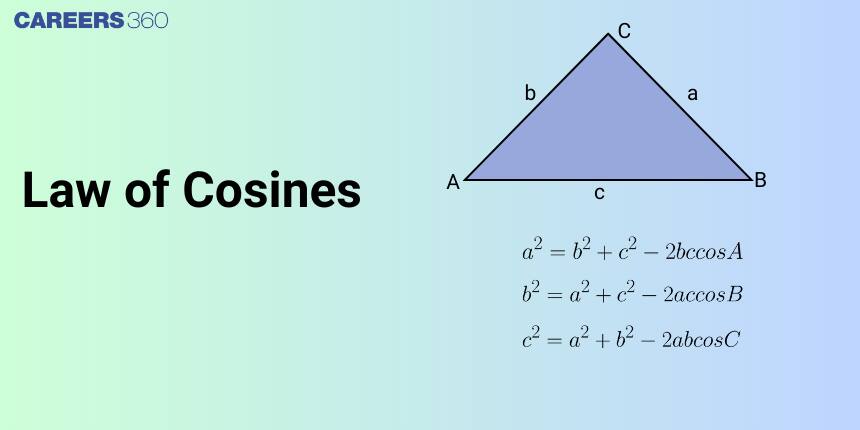
In $\triangle A B C$, the angles are denoted by capital letters $A, B$, and $C$ and the length of the sides opposite to these angles are denoted by small letters $a, b$, and $c$ respectively.

The following symbols in relation to $\triangle \mathrm{ABC}$ are universally adopted.
Angles: $\angle B A C=A, \angle A B C=B, \angle B C A=C$
Sides: $A B=c, A C=b$, and $B C=a$
Semi-perimeter of the $\triangle A B C$, is

$
s=\frac{a+b+c}{2}
$

and it is denoted by $s$. So, the perimeter of $\triangle A B C$ is $2 s=a+b+c$.

The area of a triangle is denoted by S or Δ.

For any $\triangle A B C$,

• $\mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ}$
• $a+b>c, b+c>a$ and $c+a>b$
• $a>0, b>0, c>0$

Law of Cosines: definition

The Law of Cosines states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle.

Cosine Rule

The law of cosine also called the cosine rule is used to connect the side of a triangle with the angle. If we know the three sides of the triangle then by using the cosine rule we can find the cosine of the three angles of a triangle.

For a triangle ABC with angles A, B, and C, and opposite corresponding sides a, b, and c, respectively, the Law of Cosines is given as three equations.

$\cos A=\frac{b^2+c^2-a^2}{2 b c} \quad \cos B=\frac{a^2+c^2-b^2}{2 a c} \quad \cos C=\frac{a^2+b^2-c^2}{2 a b}$

Proof:

Drop a perpendicular from C to the x -axis (this is the altitude or height). Recalling the basic trigonometric identities, we know that

$
\cos \theta=\frac{x(\text { adjacent })}{b(\text { hypotenuse })} \text { and } \sin \theta=\frac{y(\text { opposite })}{b(\text { hypotenuse })}
$
In terms of $\theta, x=b \cos \theta$ and $y=b \sin \theta$. The $(x, y)$ point located at $C$ has coordinates $(b \cos \theta, b \sin \theta)$.
Using the side $(\mathrm{x}-\mathrm{c})$ as one leg of a right triangle and y as the second leg, we can find the length of hypotenuse a using the Pythagoras Theorem. Thus,

$
\begin{aligned}
a^2= & (x-c)^2+y^2 \\
= & (b \cos \theta-c)^2+(b \sin \theta)^2 \\
& \quad[\text { Substitute }(b \cos \theta) \text { for } x \text { and }(b \sin \theta) \text { for } y] \\
= & \left(b^2 \cos ^2 \theta-2 b c \cos \theta+c^2\right)+b^2 \sin ^2 \theta
\end{aligned}
$

[Expand the perfect square.]

$
=b^2 \cos ^2 \theta+b^2 \sin ^2 \theta+c^2-2 b c \cos \theta
$

[Group terms noting that $\cos ^2 \theta+\sin ^2 \theta=1$ ]

$
=b^2\left(\cos ^2 \theta+\sin ^2 \theta\right)+c^2-2 b c \cos \theta
$

$\left[\right.$ Factor out $\left.b^2\right]$

$
a^2=b^2+c^2-2 b c \cos \theta
$
Now as $\theta$ equals angle $A$
In triangle ABC,

$
\begin{aligned}
& a^2=b^2+c^2-2 b c \cdot \cos A \\
& \cos A=\frac{b^2+c^2-a^2}{2 b c}
\end{aligned}
$

The above proof does not change if angle A is a right angle or an obtuse angle.

Similarly, we can derive formulae for cos B and cos C.

Note:

1) If the lengths of the three sides of a triangle are known, we can find all the angles by using the cosine rule.

$
\text { 2) If two sides (say } \mathrm{b} \text { and } \mathrm{c} \text { ) and the included angle } \mathrm{A} \text { are given, the cosine rule } \cos \mathrm{A}=\frac{\left(b^2+c^2-a^2\right)}{(2 b c)} \text { will give us a, and then knowing a, } \mathrm{b}, \mathrm{c} \text { we can find } \mathrm{B} \text { and } \mathrm{C} \text { by the cosine rule. }
$

Applications of Cosine Law

1) With the help of cosine law, we can find the angle of a triangle if its three sides are given.

2) We can use cosine law to find the side length of the triangle if it's all three angles are known or one angle and two side lengths are known.

Summary

The cosine rule connects the side of the triangle with the cosine of the angle. So, knowing about the cosine rule is important as it helps us to find the angle of a triangle if three sides are given or the side of a triangle if angles are given. It is the tool that makes the calculation easier.

Recommended Video :

Solved Examples Based on Cosine Rule

Example 1: In a triangle ABC, if cos A + 2 cos B + cos C = 2 and the lengths of the sides are opposite to the angles A and C are 3 and 7 respectively, then cos A – cos C is equal to: [JEE MAINS 2023]

Solution:

$
\begin{aligned}
& \cos \mathrm{A}+\cos \mathrm{C}=2(1-\cos \mathrm{B}) \\
& 2 \cos \frac{\mathrm{A}+\mathrm{C}}{2} \cos \frac{\mathrm{A}-\mathrm{C}}{2}=4 \sin ^2 \mathrm{~B} / 2 \\
& \text { as } \cos \left(\frac{\mathrm{A}+\mathrm{C}}{2}\right)=\sin \frac{B}{2} \\
& \text { so } \cos \frac{\mathrm{A}-\mathrm{C}}{2}=2 \sin \frac{B}{2} \\
& 2 \cos \mathrm{B} / 2 \cos \frac{\mathrm{A}-\mathrm{C}}{2}=4 \sin \mathrm{B} / 2 \cos \mathrm{B} / 2 \\
& 2 \sin \left(\frac{\mathrm{A}+\mathrm{C}}{2}\right) \cos \left(\frac{\mathrm{A}-\mathrm{C}}{2}\right)=4 \sin \mathrm{B} / 2 \cos \mathrm{B} / 2 \\
& \sin \mathrm{A}+\sin \mathrm{C}=2 \sin \mathrm{B} \\
& \mathrm{a}+\mathrm{c}=2 \mathrm{~b} \Rightarrow \mathrm{a}=3, \mathrm{c}=7, \mathrm{~b}=5
\end{aligned}
$
$
\begin{aligned}
& \cos \mathrm{A}-\cos \mathrm{C}=\frac{\mathrm{b}^2+\mathrm{c}^2-\mathrm{a}^2}{2 \mathrm{bc}}-\frac{\mathrm{a}^2+\mathrm{b}^2-\mathrm{c}^2}{2 \mathrm{ab}} \\
& =\frac{25+49-9}{70}-\frac{9+25-49}{30} \\
& \frac{65}{70}+\frac{1}{2}=\frac{20}{14}=\frac{10}{7}
\end{aligned}
$

Hence, the answer is $\frac{10}{7}$

Example 2:

Given $\frac{b+c}{11}=\frac{c+a}{12}=\frac{a+b}{13}$ for a $\triangle A B C$ with usual notation.
If $\frac{\cos A}{\alpha}=\frac{\cos B}{\beta}=\frac{\cos C}{\gamma}$, then the ordered triad $(\alpha, \beta, \gamma)$ has a value :
[JEE MAINS 2019]
Solution
Cosine Rule - Cosine Rule - null

$
\begin{aligned}
& b+c=11 \lambda \\
& a+c=12 \lambda \\
& a+b=13 \lambda \\
& =>a=7 \lambda, b=6 \lambda, c=5 \lambda
\end{aligned}
$
Using Cosine Formula,

$
\begin{aligned}
& \cos A=\frac{1}{5}, \cos B=\frac{19}{35}, \cos C=\frac{5}{7} \\
& \alpha: \beta: \gamma=7: 19: 25
\end{aligned}
$
Hence, the answer is $7: 19: 25$.

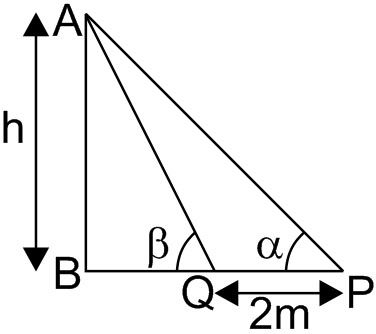
Example 3: The angle of elevation of the top of a vertical tower from a point P on the horizontal ground was observed to be $\alpha$ After moving a distance 2 meters from P towards the foot of the tower, the angle of elevation changes to $\beta$ Then the height of the tower (in meters) is [JEE MAINS 2014]

Solution

$
\begin{aligned}
& \text { In } \triangle A P B, \tan \alpha=\frac{A B}{B P} \\
& \Rightarrow B P=\frac{h}{\tan \alpha}=\frac{h \cos \alpha}{\sin \alpha} \\
& \text { In } \triangle A Q B, \tan \beta=\frac{A B}{B Q} \\
& \Rightarrow B Q=\frac{h \cos \beta}{\sin \beta}
\end{aligned}
$
Now, $P Q=2$

$
\begin{aligned}
& \Rightarrow P B-Q B=2 \\
& \Rightarrow h\left[\frac{\cos \alpha}{\sin \alpha}-\frac{\cos \beta}{\sin \beta}\right]=2 \\
& \Rightarrow h \frac{[\sin (\beta-\alpha)]}{\sin \alpha \sin \beta}=2 \\
& \Rightarrow h=\frac{2 \sin \alpha \sin \beta}{\sin (\beta-\alpha)}
\end{aligned}
$
Hence, the answer is $\frac{2 \sin \alpha \sin \beta}{\sin (\beta-\alpha)}$

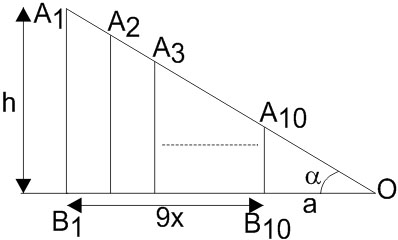
Example 4: Let 10 vertical poles standing at equal distances on a straight line, subtend the same angle of elevation at a point O on this line and all the poles are on the same side of O. If the height of the longest pole is ‘h’ and the distance of the foot of the smallest pole from O is ‘a’, then the distance between two consecutive poles is [JEE MAINS 2015]

Solution

For all poles to subtend the same angle, the longest pole must be farthest, the smallest pole must be nearest, while all other poles are arranged in ascending order of height. Let the distance between 2 consecutive poles be x. Then, $B_1 B_{10}=9 x$

$
\begin{aligned}
& \text { In, } \Delta A_1 B_1 O, \tan \alpha=\frac{A_1 B_1}{B_1 O}=\frac{h}{B_1 B_{10}+B_{10} O} \\
& \tan \alpha=\frac{h}{9 x+a} \\
& \frac{\sin \alpha}{\cos \alpha}=\frac{h}{9 x+a} \\
& \Rightarrow 9 x \sin \alpha+a \sin \alpha=h \cos \alpha \\
& \Rightarrow x=\frac{h \cos \alpha-a \sin \alpha}{9 \sin \alpha} \\
& \text { Hence, the answer is } \frac{h \cos \alpha-a \sin \alpha}{9 \sin \alpha}
\end{aligned}
$

Example 5: Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that $\mathrm{AP}=2 \mathrm{AB}$. If $\angle B P C=\beta$, then tan $\beta$ is equal to :
[JEE MAINS 2017]
Solution

Solution

Height and Distances -The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.

Let, AC=CB=h, AB=2h and AP=4h

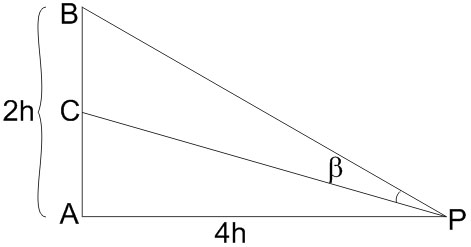
Now, $\tan \angle B P A=\frac{2 h}{4 h}=\frac{1}{2}$
$\tan \angle C P A=\frac{h}{4 h}=\frac{1}{4}$
$\tan \beta=\tan (\angle B P A-\angle C P A)=\frac{\tan (\angle B P A)-\tan (\angle C P A)}{1+\tan (\angle B P A) \tan (\angle C P A)}$
$=\frac{\frac{1}{2}-\frac{1}{4}}{1+\frac{1}{8}}=\frac{\frac{1}{4}}{\frac{9}{8}}=\frac{2}{9}$
$\tan \beta=\frac{2}{9}$
Hence, the answer is $\frac{2}{9}$