Length of Tangent, Subtangent, Normal and Subnormal

Length of Tangent, Normal, Subtangent, and Subnormal is an important concept in calculus. It is useful in understanding the relationship between curves and their slopes. The tangent line to the curve is a straight line that touches a curve at a single point without crossing it at that point. These concepts of Tangents and slopes have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

In this article, we will cover the concept of the Length of Tangent, Normal, Subtangent, and Subnormal. This topic falls under the broader category of Calculus, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of four questions have been asked on this topic in JEE Main from 2013 to 2023, including one question in 2014, one question in 2015, one question in 2019, and one in 2021.

Tangent to the Curve at point:

Tangent

The tangent to a curve at a point $P$ on it is defined as the limiting position of the secant $P Q$ as the point $Q$ approaches the point $P$ provided such a limiting position exists.
The slope of the tangent to the curve $\mathrm{y}=\mathrm{f}(\mathrm{x})$ at the point $\left(\mathrm{x}_0, \mathrm{y}_0\right)$ is given by $\left.\frac{d y}{d x}\right]_{\left(x_0, y_0\right)} \quad\left(=\mathrm{f}^{\prime}\left(\mathrm{x}_0\right)\right)$. So the equation of the tangent at $\left(\mathrm{x}_0, \mathrm{y}_0\right)$ to the curve $\mathrm{y}=\mathrm{f}(\mathrm{x})$ is given by $y-y_0=f^{\prime}\left(x_0\right)\left(x-x_0\right)$.

NORMAL

The normal to the curve at any point P on it is the straight line which passes through P and is perpendicular to the tangent to the curve at P

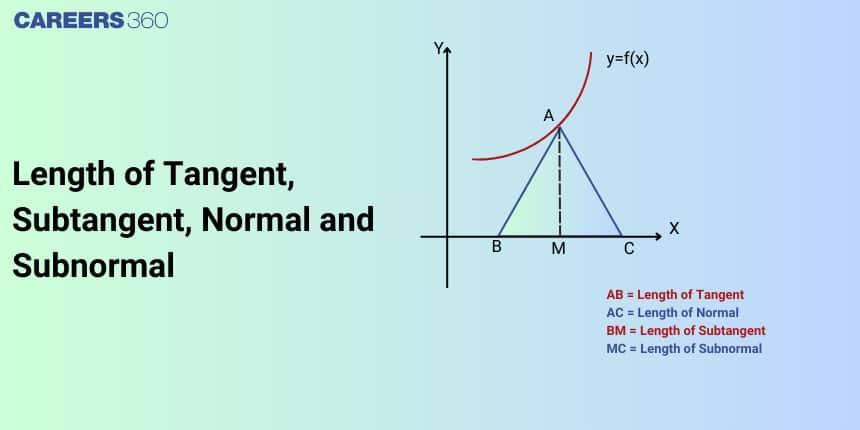
Length of Tangent, Normal, Subtangent and Subnormal

Length of Tangent:

The length of the portion lying between the point of tangency i.e. the point on the curve from which a tangent is drawn and the point where the tangent meets the $x$-axis. Here point of tangency is $P\left(x_0, y_0\right)$
In the figure, the length of segment PT is the length of the tangent.
In $\triangle \mathrm{PTS}$

$
\begin{aligned}
\mathrm{PT} & =|y \cdot \csc \theta|=|y| \sqrt{1+\cot ^2 \theta} \\
& =|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dx}}{\mathrm{dy}}\right)_{\left(\mathrm{x} 0, \mathrm{y}_0\right)}}
\end{aligned}
$

Length of Normal:

A segment of normal PN is called length of Normal.
In $\triangle P S N$

$
\begin{aligned}
\mathrm{PN} & =\left|y \cdot \csc \left(90^{\circ}-\theta\right)\right|=|y \cdot \sec \theta| \\
& =|\mathrm{y}| \sqrt{1+\tan ^2 \theta}=|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{(\mathrm{x} 0, \mathrm{y} 0)}}
\end{aligned}
$

Length of Subtangent:

The projection of the segment PT along the x-axis is called the length of the subtangent. In the figure, ST is the length of the subtangent.

In ΔPST

$\begin{aligned} \mathrm{ST} & =|y \cdot \cot \theta|=\left|\frac{y}{\tan \theta}\right| \\ & =\left|\mathrm{y} \cdot \frac{\mathrm{dx}}{\mathrm{dy}}\right|\end{aligned}$

Length of Subnormal:

$
\begin{aligned}
&\text { The projection of the segment PN along the } \mathrm{x} \text {-axis is called the length of the subnormal. In the figure, } \mathrm{SN} \text { is the length of }\\
&\begin{aligned}
& \operatorname{In} \triangle \mathrm{PSN} \\
& \mathrm{SN}=\left|y \cdot \cot \left(90^{\circ}-\theta\right)\right|=|y \cdot \tan \theta| \\
&=\left|\mathrm{y} \cdot \frac{\mathrm{dy}}{\mathrm{dv}}\right|
\end{aligned}
\end{aligned}
$

Solved Examples Based On Length of tangents, normal, subtangent, and subnormal:

Example 1: If the Rolle's theorem holds for the function $f(x)=2 x^3+a x^2+b x$ in the interval $[-1,1]$ for the point $c=\frac{1}{2}$ then the value of $2 a+b$ is :
[JEE Main 2014]
1) -1
2) 1
3) 2
4) -2

Solution
As we have learned
Rolle's Theorems - $\square$
Let $f(x)$ be a function of $x$ subject to the following conditions.
1. $\mathrm{f}(\mathrm{x})$ is continuous function of $x: x \in[a, b]$
2. $\mathrm{F}(\mathrm{x})$ is exists for every point: $x \epsilon[a, b]$
3. $f(a)=f(b)$ then $f^{\prime}(c)=0$ such that $a<c<b$.

Geometrical interpretation of Rolle's theorem -

Let f(x) be a function defined on [a, b] such that the curve y = f(x) is continuous between points {a, f(a)} and {b, f(b)} at every points on the curve encept at the end point it is possible to draw a unique tangent and ordinates at x = a and x = b are equal f(a) = f(b).

$
\begin{aligned}
&\text { - wherein, We have }\\
&\begin{aligned}
& f^{\prime}(1 / 2)=\frac{f(1)-f(-1)}{2}=0 \\
\Rightarrow & \left.\left(6 x^2+2 a x+b\right)\right|_{x=1 / 2} \\
& \frac{2+a+b-(-2+a-b)}{2}=0 \\
\Rightarrow & 3 / 2+a+b=\frac{4+2 b}{2}=0 \\
\Rightarrow & 3+2 a+2 b=4+2 b=0 \\
\Rightarrow & a=1 / 2 \text { and } b=-2 \\
\therefore & 2 a+b=-1
\end{aligned}
\end{aligned}
$

Example 2: If the tangent to the curve $y=x^3$ at the point $P\left(t, t^3\right)$ meets the curve again at Q, then the ordinate of the point which divides PQ internally in the ratio $1: 2$ is:
[JEE Main 2021]
1) $-2 t^3$
2) $-t^3$
3) 0
4) $2 t^3$

Solution
Equation of tangent at $\mathrm{P}\left(\mathrm{t}, \mathrm{t}^3\right)$

$
\left(y-t^3\right)=3 t^2(x-t)
$

now solve the above equation with

$
y=x^3
$

$
\begin{aligned}
&\begin{aligned}
& \text { By }(1) \&(2) \\
& x^3-t^3=3 t^2(x-t) \\
& \mathrm{x}^2+\mathrm{xt}+\mathrm{t}^2=3 \mathrm{t}^2 \\
& \mathrm{x}^2+\mathrm{xt}-2 \mathrm{t}^2=0 \\
& (x-t)(x+2 t)=0 \\
& \Rightarrow x=-2 t \Rightarrow Q\left(-2 t,-8 t^3\right)
\end{aligned}\\
&\text { Ordinate of required point }\\
&=\frac{2 t^3+\left(-8 t^3\right)}{3}=-2 t^3
\end{aligned}
$

Hence, the answer is the option (1).

Example 3: The shortest distance between the line $\mathrm{y}=\mathrm{x}$ and the curve $y^2=x-2$ is.
[JEE Main 2015]
1) $\frac{7}{4 \sqrt{2}}$
2) $\frac{7}{2 \sqrt{2}}$
3) $\frac{7}{4 \sqrt{3}}$
4) $\frac{5}{4 \sqrt{2}}$

Solution

Line $\mathrm{y}=\mathrm{x}$
Eq. of tangent to $\mathrm{y}^2=\mathrm{x}-2$
$y^2=x-2$
$2 \mathrm{yy}^{\prime}=1$
$\mathrm{y}^{\prime}=\frac{1}{2 \mathrm{y}}=$ slope
Tangent at $P$ is parallel to the line $x=y$
so, slope should be equal

$
\mathrm{y}^{\prime}=1=\frac{1}{2 \mathrm{y}} \Rightarrow \mathrm{y}=\frac{1}{2}
$

put the value of $y$ in the curve $y^2=x-2$

$
\left(\frac{1}{2}\right)^2=x-2 \Rightarrow x=\frac{9}{4}
$

so, $\mathrm{P}=\left(\frac{9}{4}, \frac{1}{2}\right)$
Perpendicular distance from the point $P$ to the line $y=x$

$
\left|\frac{\left(\frac{9}{4}-\frac{1}{2}\right)}{\sqrt{1^2+1^2}}\right|=\frac{7}{4 \sqrt{2}}
$
Hence, the answer is option (1).

Example 4: If Rolle's theorem holds for the function $f(x)=2 x^3+b x^2+c x, x \in[-1,1]$ at the point $x=\frac{1}{2}$, then $2 b+c$ equals:
[JEE Main 2019]
1) -1
2) -2
3) -3
4) -4

Solution
Rolle's Theorems
Let $f(x)$ be a function with the following properties
1. $f(x)$ is a continuous function in $[a, b]$
2. $\underline{\underline{f}}^{\prime}(\mathrm{x})$ exists for every point in (a,b)
3. $f(a)=f(b)$

Then there is at least one c lying in $(a, b)$ such that $\underline{f}(c)=0$
Now,

$
f(x)=2 x^3+b x^2+c x
$

It is continuous and differentiable in any interval as it is a polynomial, hence it is continuous in $[-1,1]$ and differentiable in $(-1,1)$
Now $f(-1)=f(1)$
where, $f(1)=2+b+c$ and $f(-1)=-2+b-c$

$
\begin{aligned}
& \Rightarrow b+c+2=b-2-c \\
& \Rightarrow c+2=0 \\
& \therefore c=-2
\end{aligned}
$
Also

$
f^{\prime}(x)=6 x^2+2 b x+c
$
As Rolle's Theorem is satisfied at $x=1 / 2$, hence $f^{\prime}(1 / 2)=0$

$
\begin{aligned}
& 0=6\left(\frac{1}{2}\right)^2+b \times 2 \times \frac{1}{2}-2 \\
& 0=\frac{6}{4}+b-2 \\
& \mathrm{~b}=1 / 2
\end{aligned}
$
So, $2 b+c=-1$

Hence the answer is the option (1)

Example 5 : Length of normal drawn to the curve $x y=16$ at its point $(4,4)$ equals?
1) $6 \sqrt{2}$
2) $5 \sqrt{2}$
3) $4 \sqrt{2}$
4) $3 \sqrt{2}$

Solution
As we know, the length of Normal $=y_o \sqrt{1+\left(y^{\prime}\right)^2}$
Here the curve is

$
\begin{aligned}
& x y=16 \\
& \Rightarrow y=\frac{16}{x} \\
& \Rightarrow y^{\prime}=-16 / x^2 \\
& \Rightarrow y^{\prime} \text { at }(4,4)=-1 \\
& \therefore \text { Length of normal }=4 \sqrt{1+1}=4 \sqrt{2}
\end{aligned}
$

Summary

Tangent, slope, and normal are important in the concept of Calculus. The slope of the tangent at a point on the curve is given by the derivative, and the equation of the tangent can be derived using this slope. These concepts are essential for analyzing and understanding the behaviour of curves and surfaces.