Matrices

A matrix is a rectangular array of objects. These matrices can be visualised in day-to-day applications where we use matrices to represent a military parade or a school assembly or vegetation. Matrices have become one of the most important tools in mathematics. These matrices are used in various domains like computer science, cryptography, physics, biology, chemistry, statistics and economics, etc.

This article is about the concept of Matrices class 12. The matrices chapter is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE, BCECE, and more.

Introduction to Matrices

Matrices are useful for representing coefficients in systems of linear equations. Matrix notations and operations are used in electronic spreadsheet programs on computers, which in turn are used in different areas of business like budgeting, sales projection, cost estimation, and in science, for analyzing the results of an experiment etc. Interestingly, many geometric operations such as magnification, rotation and reflection through a plane can also be represented mathematically by matrices. Economists use matrices for social accounting, input-output tables and in the study of inter-industry economics. Matrices are also used in communication theory and network analysis in electrical engineering. They are also used in Cryptography. Now, lets look into the concept of matrices and its properties in detail in this article.

Matrix Definition

A matrix is a rectangular array of objects represented in rows and columns inside closed brackets [ ]. The entries of a matrix may be real or complex numbers or functions of one variable (such as polynomials, trigonometric functions or a combination of them) or more variables or any other object. Usually, matrices are denoted by capital letters A, B, C, ... etc.

General form of a matrix

If a matrix $A$ has $m$ rows and $n$ columns, then it is written as $A=\left[a_{i j}\right]_{m \times n}, 1 \leq i \leq m, 1 \leq j \leq n$.

$A=\left[a_{i j}\right]_{m \times n}=\left[\begin{array}{cccccc}a_{11} & a_{12} & \cdots & a_{1 j} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 j} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ a_{i 1} & a_{i 2} & \cdots & a_{i j} & \cdots & a_{i n} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m j} & \cdots & a_{m n}\end{array}\right] \leftarrow$ Row 1

Order of a Matrix

The order of the matrix is the number of rows and columns of the matrix. If a matrix has ' $m$ ' rows and ' $n$ ' columns, then the order of the matrix is said to be ' $m \times n$ '.

For example, the matrix given below has $3$ rows and $4$ columns. So, the order of the matrix is $3 \times 4$ and the matrix has $12$ elements.

The order of a matrix is determined by the number of rows and columns it contains. For instance, if a matrix has "$m$" rows and "$n$" columns, its order is represented as "$m × n$".

Order of matrix = Number of row $\times$ Number of column

Examples:

1. $\left[\begin{array}{ccc}2 & 4 & -3 \\ 5 & 4 & 6\end{array}\right]$
2. $\left[\begin{array}{cc}2 & 4 i+3 \\ 5 & 4 \\ 3 i & -75\end{array}\right]$
3. $\left[\begin{array}{c}2 \\ -5 \\ 3 i \\ 71\end{array}\right]$

In the first matrix above, elements $2, 4$ and $-3$ lie in the first row and $5, 4$ and $6$ in the second row. Also, $2,$ and $5,$ lie in the first column, $4,4$ in the second column, and $-3, 6$ in the third column. Therefore, the order of a matrix is $2 \times 3$

Similarly, the Second matrix has order $3 \times 2$ and the third matrix has order $4 \times 1$

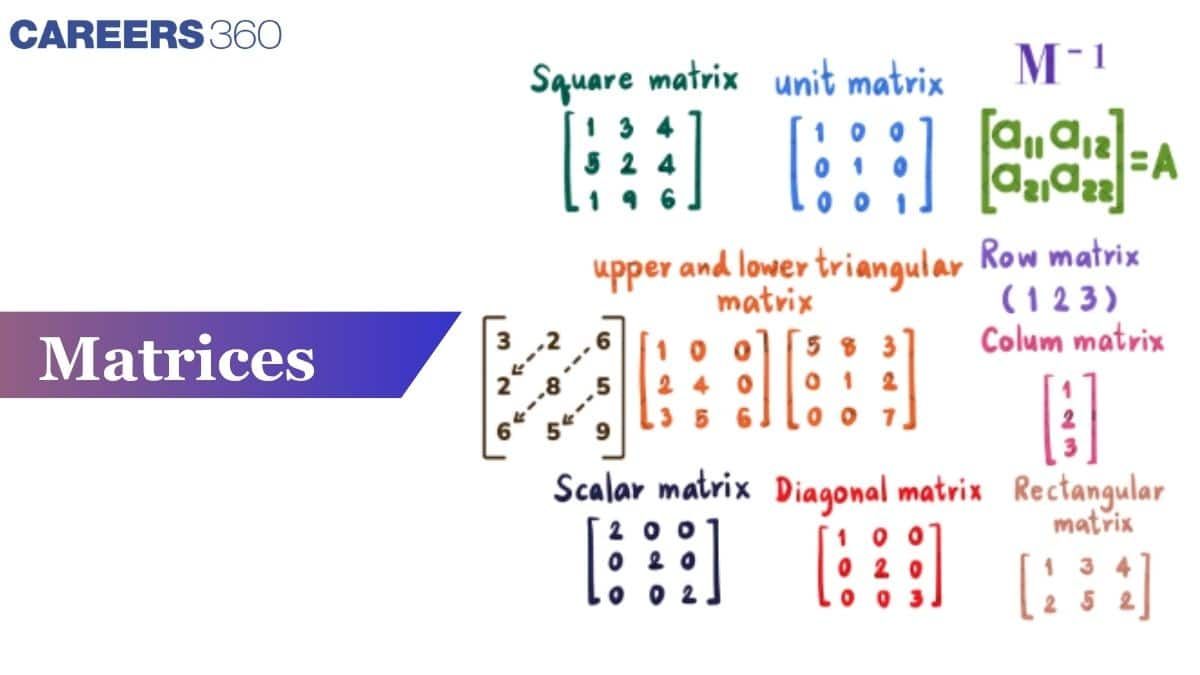
Types of Matrices

Matrices are classified based on the order of the matrices. The types of matrices are,

Row matrix: A matrix containing only one row is called a row matrix. So a matrix $A=\left[a_{i j}\right]_{m \times n}$ is said to be a row matrix when $m=1$.

It can be denoted by

$
\left[\begin{array}{llllll}
a_{11} & a_{12} & a_{13} & \ldots & \ldots & a_{1 n}
\end{array}\right]_{1 \times \mathrm{n}}
$

For example, $\left[\begin{array}{llll}1 & 32 & 81 & -32\end{array}\right]$ has only 1 row. It has order $1 \times 4$

Column matrix: A matrix containing only one column is known as a column matrix. So a matrix $A=\left[a_{i j}\right]_m \times n$ is said to be a column matrix when $n=1$. It is denoted by $\left[\begin{array}{c}a_{11} \\ a_{21} \\ a_{31} \\ \cdots \\ \cdots \\ a_{m 1}\end{array}\right]_{\mathrm{m} \times 1}$

For example, $\left[\begin{array}{c}2 \\ 32 \\ 3 \\ 7\end{array}\right]$

This matrix has order 4 x 1

Note: A matrix that contains only one row or one column is also known as a vector i.e. row vectors and column vectors.

Equal Matrices: Two matrices are said to be equal if they have the same order and each element of one matrix is equal to the corresponding elements of another matrix or we can say $a_{i j}=b_{i j}$ where $\mathrm{a}$ is the element of one matrix and $\mathrm{b}$ is the element of another matrix.

Square matrix: The square matrix is the matrix in which the number of rows $=$ number of columns. So a matrix $A=\left[a_{i j}\right]_m \times n$ is said to be a square matrix when $\mathrm{m}=\mathrm{n}$.
Example,
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]_{3 \times 3} \text { or, }\left[\begin{array}{cc}
2 & -4 \\
7 & 3
\end{array}\right]_{2 \times 2}
$
$A+A^{\prime}$ is a symmetric matrix and $A-A^{\prime}$ is a skew-symmetric matrix for a square matrix with real number elements.
Symmetric and skew-symmetric matrix added together yields a square matrix. $1 / 2\left(A+A^{\prime}\right)+1 / 2\left(A-A^{\prime}\right)$ equals $A$.

Rectangular matrix: Rectangular matrix is the matrix in which is the number of rows $\neq$ and number of columns.
So a matrix $A=\left[a_{i j}\right] m \times n$ is said to be a rectangular matrix when $\mathrm{m} \neq \mathrm{n}$.
$
\text { For example, }\left[\begin{array}{llll}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34}
\end{array}\right]_{3 \times 4}
$

Null matrix/ Zero Matrix: A matrix whose all elements are 0, is called a null matrix. It is represented by 'o'
$\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{m} \times \mathrm{n}$, where $\mathrm{a}_{\mathrm{ij}}=0$
For example, $\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right],\left[\begin{array}{llll}0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{array}\right]$

Diagonal matrix: A square matrix is said to be a diagonal matrix, if all its elements except the diagonal elements are zero.
So, a matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is a diagonal matrix if $\mathrm{a}_{\mathrm{ij}}=0$, whenever $\mathrm{i} \neq \mathrm{j}$ and $\mathrm{m}=\mathrm{n}$.

Diagonal matrix: $\left[\begin{array}{ccc}a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33}\end{array}\right]$
A diagonal matrix of order $\mathrm{n} \times \mathrm{n}$ having diagonal elements as $\mathrm{d}_1, \mathrm{~d}_2, \mathrm{~d}_3 \ldots \ldots \ldots, \mathrm{d}_{\mathrm{n}}$ is denoted by $\operatorname{diag}\left[d_1, d_2, d_3 \ldots \ldots . ., d_n\right]$
For example,
$
A=\left[\begin{array}{cc}
6 & 0 \\
0 & -7
\end{array}\right] \quad B=\left[\begin{array}{ccc}
2 & 0 & 0 \\
0 & -9 & 0 \\
0 & 0 & 3
\end{array}\right]
$
so, we can write
$
\mathrm{A}=\operatorname{diag}[6,-7] \text { and } \mathrm{B}=\operatorname{diag}[2,-9,3]
$

Scalar matrix: A diagonal matrix whose all the diagonal elements are equal is called a scalar matrix.
$
A=\left[\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right] \quad B=\left[\begin{array}{ccc}
-3 & 0 & 0 \\
0 & -3 & 0 \\
0 & 0 & -3
\end{array}\right]
$

For a square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$ to be scalar matrix
$
\mathrm{a}_{\mathrm{ij}}= \begin{cases}0, & i \neq j \\ c, & i=j\end{cases}
$

Where $\mathrm{c}$ is not equal to 0

Unit or Identity Matrix: A diagonal matrix of order $\mathrm{n}$ whose all the diagonal elements are equal to one is called an identity matrix of order $\mathrm{n}$. It is represented as $I$.

So, a square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$ is an Identity matrix if
$
\mathrm{a}_{\mathrm{ij}}= \begin{cases}0, & i \neq j \\ 1, & i=j\end{cases}
$

For example,
$
\mathrm{I}_3=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]
$

The product of the conjugate transpose of a unitary matrix, with the unitary matrix, gives an identity matrix.

Upper triangular matrix: A square matrix whose all elements below the principal diagonal are zero is called an upper triangular matrix.
or $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is said to be upper triangular if $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}=0$ when $\mathrm{i}>\mathrm{j}$.
$
\text { Upper triangular matrix: }\left[\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\
0 & a_{22} & a_{23} & a_{24} & a_{25} \\
0 & 0 & a_{33} & a_{34} & a_{35} \\
0 & 0 & 0 & a_{44} & a_{45} \\
0 & 0 & 0 & 0 & a_{55}
\end{array}\right]
$

Lower triangular matrix: A square matrix whose all elements above the principal diagonal is zero is called a lower triangular matrix.

Lower triangular matrix:
$
\left[\begin{array}{ccccc}
a_{11} & 0 & 0 & 0 & 0 \\
a_{21} & a_{22} & 0 & 0 & 0 \\
a_{31} & a_{32} & a_{33} & 0 & 0 \\
a_{41} & a_{42} & a_{43} & a_{44} & 0 \\
a_{51} & a_{52} & a_{53} & a_{54} & a_{55}
\end{array}\right]
$

Symmetric matrix: A square matrix $A=\left[a_{i j}\right]_{n \times n}$ is said to be symmetric if $A^{\prime}=A$,
$
\begin{aligned}
& \text { i.e., } \mathrm{a}_{\mathrm{ij}}=\mathrm{a}_{\mathrm{ji}} \forall \mathrm{i}, \mathrm{j} \\
& \mathrm{A}=\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right] \text { then } \mathrm{A}^{\prime}=\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right]
\end{aligned}
$

Clearly, $A=A^{\prime}$, hence $A$ is a symmetric matrix

Skew-symmetric matrix:
A square matrix $A=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is said to be skew-symmetric if $\mathrm{A}^{\prime}=-\mathrm{A}$
$
\text { i.e. } A^{\prime}=-A \text {, i.e., } a_{i j}=-a_{j i} \forall i, j
$

Now if we put $\mathrm{i}=\mathrm{j}$, we have
$
\begin{aligned}
& \mathrm{a}_{\mathrm{ii}}=-\mathrm{a}_{\mathrm{ii}}, \\
& \therefore 2 \mathrm{a}_{\mathrm{ii}}=0 \Rightarrow \mathrm{a}_{\mathrm{ii}}=0 \forall \mathrm{i}^{\prime} \mathrm{s}
\end{aligned}
$

Hermitian matrix
A square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{n} \times \mathrm{n}$ is said to be a Hermitian matrix if $a_{i j}=\overline{a_{j i}} \forall \mathrm{i}, \mathrm{j}$,
i.e. $A=A^\theta, \quad\left[\right.$ where $A^\theta$ is conjugate transpose of matrix $\left.A\right]$

Skew-hermitian matrix
A square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{n} \times \mathrm{n}$ is said to be a Skew-Hermitian matrix if $a_{i j}=-\overline{a_{i j}} \forall \mathrm{i}, \mathrm{j}$, i.e. $\mathrm{A}^\theta=-\mathrm{A}, \quad\left[\right.$ where $\mathrm{A}^\theta$ is conjugate transpose of matrix $\left.\mathrm{A}\right]$

Orthogonal matrix
A square matrix is said to be an orthogonal matrix if $A A^{\prime}=I$, where $I$ is the identity matrix.

Singular and Non-Singular matrix

A square matrix is called a singular matrix if its determinant is 0 otherwise it is called a non-singular matrix. Let's say A is a square matrix then it is singular if |A| = 0, otherwise, it will be non-singular if |A| ≠ 0.

Idempotent matrix
A square matrix is said to be an idempotent matrix if it satisfies the condition $A^2=A$

Nilpotent matrix

If $A$ satisfies the condition $Ak = 0$ and $Ak-1 ≠ 0$, then A is called a nilpotent matrix $k$ is known as the order of nilpotent matrix A.

Involutory matrix
If A satisfies the condition $A^2=A$, where $\mathrm{I}$ is the identity matrix then $\mathrm{A}$ is called the involutory matrix.

Note: $A=A^{-1}$ for involutory matrix.

Periodic matrix

If a square matrix $A$ satisfies the relation $A^{k+1}=A$, where $k$ is a +ve integer. Then $A$ is called a periodic matrix. If k is the least +ve integer for which this condition is satisfied then k is called the period of $A$.

For $k = 1$, we get $A^2=A$, which is the condition for the idempotent matrix, so the period of the idempotent matrix $=1$.

Matrix Operations

The addition, subtraction, and multiplication of matrices are the basic algebraic matrix operations.

Addition of matrices

Two matrices can be added only when they are of the same order

If two matrices of $A$ and $B$ are of the same order, they are said to be conformable for addition.

If $A$ and $B$ are matrices of order $m \times n$, then their sum will also be a matrix of the same order and in addition, corresponding elements of $ A$ and $B$ get added.

So if $A=\left[a_{i j}\right]_{m \times n}, B=\left[b_{i j}\right]_{m \times n}$ Then, $A+B=\left[a_{i j}+b_{i j}\right]_{m \times n}$ for all $\mathrm{i}, \mathrm{j}$
Example:
$
\begin{aligned}
\mathrm{A} & =\left[\begin{array}{lll}
10 & 20 & 30 \\
20 & 30 & 40 \\
30 & 40 & 50
\end{array}\right], \quad \mathrm{B}=\left[\begin{array}{lll}
50 & 40 & 30 \\
40 & 30 & 20 \\
30 & 20 & 10
\end{array}\right] \\
\mathrm{A}+\mathrm{B} & =\left[\begin{array}{lll}
10+50 & 20+40 & 30+30 \\
20+40 & 30+30 & 40+20 \\
30+30 & 40+20 & 50+10
\end{array}\right]=\left[\begin{array}{lll}
60 & 60 & 60 \\
60 & 60 & 60 \\
60 & 60 & 60
\end{array}\right]
\end{aligned}
$

Subtraction of matrices

Two matrices can be subtracted only when they are of the same order. If $A$ and $B$ are matrices of order $m \times n$ then their difference will also be a matrix of the same order and in subtraction, corresponding elements of $A$ and $B$ get subtracted. So if

$
\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}, \mathrm{B}=\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \text { Then, } \mathrm{A}-\mathrm{B}=\left[\mathrm{a}_{\mathrm{ij}}-\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n} \text { for all } \mathrm{i}, \mathrm{j}}
$

Example:
$
\begin{aligned}
\mathrm{A} & =\left[\begin{array}{lll}
10 & 20 & 30 \\
20 & 30 & 40 \\
30 & 40 & 50
\end{array}\right], \quad \mathrm{B}=\left[\begin{array}{lll}
50 & 40 & 30 \\
40 & 30 & 20 \\
30 & 20 & 10
\end{array}\right] \\
\mathrm{A}-\mathrm{B} & =\left[\begin{array}{lll}
10-50 & 20-40 & 30-30 \\
20-40 & 30-30 & 40-20 \\
30-30 & 40-20 & 50-10
\end{array}\right]=\left[\begin{array}{ccc}
-40 & -20 & 0 \\
-20 & 0 & 20 \\
0 & 20 & 40
\end{array}\right]
\end{aligned}
$

Scalar multiplication

Let $\mathrm{k}$ be any scalar number, and $A=\left[a_{i j}\right]_{m \times n}$ be a matrix. Then the matrix is obtained by multiplying every element $\mathrm{A}$ by a scalar $\mathrm{k}$ and denoted as $kA$.
$
\begin{aligned}
& k A=\left[k a_{i j}\right]_{m \times n} \\
& \qquad \mathrm{~A}=\left[\begin{array}{ll}
2 & 6 \\
3 & 7 \\
5 & 8
\end{array}\right] \text { then, } 3 \mathrm{~A}=\left[\begin{array}{ll}
3 \times 2 & 3 \times 6 \\
3 \times 3 & 3 \times 7 \\
3 \times 5 & 3 \times 8
\end{array}\right]=\left[\begin{array}{cc}
6 & 18 \\
9 & 21 \\
15 & 24
\end{array}\right]
\end{aligned}
$

Properties of scalar multiplication

If $A$ and $B$ are two matrices and $k, l$ are scalar then
i) $k(A+B)=k A+k B$
ii) $k(A)=k(I A)=l(k A)$
iii) $(k+1) A=k A+1 A$
iv) $(-k) A=-(k A)=k(-A)$
v) $1 \mathrm{~A}=\mathrm{A},(-1) \mathrm{A}=-\mathrm{A}$

Note: $A$ and $B$ have the same order $m \times n$.

Now lets see how to multiply two matrices.

Multiplication of Matrices

Product of two matrices $A$ and $B$ can be found if the number of columns in matrix $ A$ and the number rows in matrix $B$ are equal. Otherwise, multiplication of matrices is not possible.

i) $A B$ is defined only if $\operatorname{col}(A)=\operatorname{row}(B)$
ii) $B A$ is defined only if $\operatorname{col}(B)=\operatorname{row}(A)$

If

$\begin{aligned} & \mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \\ & \mathrm{B}=\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{p}} \\ & \mathrm{C}=\mathrm{AB}=\left[\mathrm{c}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{p}} \\ & \text { Where } c_{\mathrm{ij}}=\sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{a}_{\mathrm{ij}} \mathrm{b}_{\mathrm{jk}}, 1 \leq \mathrm{i} \leq \mathrm{m}, 1 \leq \mathrm{k} \leq \mathrm{p} \\ & =a_{i 1} b_{1 k}+a_{i 2} b_{2 k}+a_{i 3} b_{3 k}+\ldots+a_{i n} b_{n k} \\ & \end{aligned}$

For example

Suppose, two matrices are given
$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{33}
\end{array}\right]_{2 \times 3} \quad \text { and } \quad \mathrm{B}=\left[\begin{array}{lll}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} & b_{32} & b_{33}
\end{array}\right]_{3 \times 3}
$

To obtain the entries in row $i$ and column j of AB, we multiply the entries in row $i$ of $\mathrm{A}$ by column $j$ in $\mathrm{B}$ and add.
given matrices $\mathrm{A}$ and $\mathrm{B}$, where the order of $\mathrm{A}$ are $2 \times 3$ and the order of $\mathrm{B}$ are $3 \times 3$, the product of $\mathrm{AB}$ will be a $2 \times 3$ matrix.To obtain the entry in row 1, column 1 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the first column in $\mathrm{B}$, and add.

$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{11} \\
b_{21} \\
b_{31}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{11}+\mathrm{a}_{12} \cdot \mathrm{b}_{21}+\mathrm{a}_{13} \cdot \mathrm{b}_{31}
$

To obtain the entry in row 1, column 2 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the second column in B and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{12} \\
b_{22} \\
b_{32}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{12}+\mathrm{a}_{12} \cdot \mathrm{b}_{22}+\mathrm{a}_{13} \cdot \mathrm{b}_{32}
$

To obtain the entry in row 1, column 3 of $\mathrm{AB}$, multiply the first row in $A$ by the third column in B, and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{13} \\
b_{23} \\
b_{33}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{13}+\mathrm{a}_{12} \cdot \mathrm{b}_{23}+\mathrm{a}_{13} \cdot \mathrm{b}_{33}
$

We proceed the same way to obtain the second row of $\mathrm{AB}$. In other words, row 2 of $\mathrm{A}$ times column 1 of $\mathrm{B}$; row 2 of A times column 2 of B; row 2 of A times column 3 of B.

When complete, the product matrix will be
$
\mathrm{AB}=\left[\begin{array}{lll}
a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31} & a_{11} \cdot b_{12}+a_{12} \cdot b_{22}+a_{13} \cdot b_{32} & a_{11} \cdot b_{13}+a_{12} \cdot b_{23}+a_{13} \cdot b_{33} \\
a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31} & a_{21} \cdot b_{12}+a_{22} \cdot b_{22}+a_{23} \cdot b_{32} & a_{21} \cdot b_{13}+a_{22} \cdot b_{23}+a_{23} \cdot b_{33}
\end{array}\right]
$

Matrix Multiplication Rules

The following matrix multiplication rules and properties can be expressed using the above-described formula and process.

• If the number of rows in $B$ equals the number of columns in $A$, then the product of two matrices $A$ and $B$ is defined.
• BA does not need to be defined if $AB$ is defined.
• Both $AB$ and $BA$ are defined if $A$ and $B$ are square matrices of the same order.
• It is not required for $AB$ to equal $BA$ if both $AB$ and $BA$ are defined.
• One of the matrices is not required to be a zero matrix in order for the product of two matrices to be a zero matrix.

Properties of Matrix Multiplication

i) Multiplication may or may not be commutative, so $AB$ may or may not be equal to $BA$
ii) Matrix multiplication is associative, meaning $A(B C)=(A B) C$
iii) Matrix multiplication is distributive over addition, mean $A(B+C)=A B+A C$ and $(B+C) A=B A+C A$
iv) If matrix multiplication of two matrices gives a null matrix then it doesn't mean that any of those two matrices was a null matrix.

$A=\left[\begin{array}{ll}0 & 2 \\ 0 & 0\end{array}\right]$ and $B=\left[\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right]$, then $A B=\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$

v) Cancellation law in matrix multiplication doesn't hold, which means $A B=A C \Rightarrow B$ $=\mathrm{C}$
vi) Matrix multiplication $A \times A$ is represented by $A^2$. Thus, $A \cdot A \cdot A \cdot A$ .........$n$ times $=A^n$.

vii) if $\mathrm{A}$ is $\mathrm{m} \times \mathrm{n}$ matrix then, $\mathrm{I}_{\mathrm{m}} \mathrm{A}=\mathrm{A}=\mathrm{AI}_{\mathrm{n}}$.

Inverse of a Matrix

A non-singular square matrix $A$ is said to be invertible if there exists a non-singular square matrix $B$ such that $
\mathrm{AB}=\mathrm{I}=\mathrm{BA}
$ and the matrix $B$ is called the inverse of matrix $A$. Clearly, $B$ should also have the same order as $A$.

Hence, $\mathrm{A}^{-1}=\mathrm{B} \Leftrightarrow \mathrm{AB}=\mathbb{I}_{\mathrm{n}}=\mathrm{BA}$

The inverse of a $2 \times 2$ Matrix
Let $A$ is a square matrix of order $2$

$
\mathrm{A}=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]
$

Then,

$
\mathrm{A}^{-1}=\frac{1}{\mathrm{ad}-\mathrm{bc}}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]
$
The inverse of a $3 \times 3$ Matrix

The inverse of $3 \times 3$ Matrix can be caluculated by the formula $A^{-1}=\frac{1}{|A|} \cdot \operatorname{adj}(A)$

Trace of a Matrix

The sum of all diagonal elements of a square matrix is called the trace of a matrix. Lying along the principal diagonal is called the trace of $A.$

The trace of the matrix is denoted by $Tr(A)$ or $tr.A$.

$
\operatorname{Tr}(\mathrm{A})=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{a}_{\mathrm{ii}}
$

Let us consider the square matrix of order $3 \times 3$ as shown below. The elements of the matrix are $a_{11}, a_{12}, a_{13}$ $\qquad$ , $a_{33}$. The principal diagonal elements are $a_{11}, a_{22}, a_{33}$. So trace of the matrix is the sum of all principal diagonal elements.
$
\begin{aligned}
& A=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right] \\
& \operatorname{Tr}(A)=a_{11}+a_{22}+a_{33}
\end{aligned}
$

Eg.
For a given matrix $\mathrm{A}$,
$
A=\left[\begin{array}{ccc}
-2 & 4 & 7 \\
8 & 3 & -1 \\
5 & -6 & 9
\end{array}\right], \operatorname{Tr}(\mathrm{A})=-2+3+9=10
$

Transpose of a Matrix

A matrix can be transposed by interchanging its rows into columns or its columns into rows. The letter "$T$" in the superscript of the matrix is used to denote the transpose of the matrix.

In simple language, the transpose of a matrix is changing its rows into columns or columns into rows.

Let $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ be a matrix, then matrix obtained by changing rows into columns or vice-versa will give transpose of $\mathrm{A}$ which is denoted as $\mathrm{A}^{\prime}$ or $\mathrm{A}^{\top}$. Hence $\mathrm{A}^{\prime}=\left[\mathrm{a}_{\mathrm{ji}}\right]_{\mathrm{n} \times \mathrm{m}}$

$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right] \Rightarrow \mathrm{A}^{\prime}=\left[\begin{array}{lll}
a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
a_{13} & a_{23} & a_{33}
\end{array}\right]
$

Example,

If, $A=\left[\begin{array}{ll}2 & 6 \\ 3 & 7 \\ 5 & 8\end{array}\right]$ then, $A^{\prime}=\left[\begin{array}{lll}2 & 3 & 5 \\ 6 & 7 & 8\end{array}\right]$

Properties of Transpose of a Matrix

If $A^{\prime}$ and $B^{\prime}$ denote the transpose of the matrices $A$ and $B$, then :

i) Transpose of the Transpose Matrix

The matrix that results from taking the transpose of the transpose matrix is equal to the original matrix. Hence $\left(A^{\prime}\right)^{\prime}=A$

ii) Addition of Transpose Matrix

The resultant transpose of the addition of two matrices $A$ and $B$ is precisely equal to the total of the transposes of $A$ and $B$ separately

Hence, $(A \pm B)^{\prime}=A^{\prime} \pm B^{\prime}$ (given that $A$ and $B$ are conformable for matrix addition)

iii) Multiplication by constant

The matrix acquired is identical to the transpose of the original matrix multiplied by the constant when a matrix is multiplied by a constant and its transpose is taken.

In other words, $(k A)^{\prime}=k A^{\prime}$

iv) Multiplication Properties of Transpose

The product of the transpose of the two matrices in reverse order equals the transpose of the product of two matrices.

That's $(A B)^{\prime}=B^{\prime} A^{\prime}($ given that $A$ and $B$ are conformable for matrix product $A B)$

Applications of Matrices

The applications of matrices include,

• Matrices are useful for representing coefficient in systems of linear equations.
• Matrix notations and operaion are used in electronic spreadsheet programs on computers which in turn are used in different areas of business like budgeting, sales, production, cost estimation, and in science, for analyzing the results of an experiment etc.
• Many geometric operations such as magnification, rotation and reflection through a plane can also be represented mathematically by matrices.
• Economists use matrices for social accounting, input-output tables and in the study of inter-industry economics.
• Matrices are also used in communication theory and network analysis in electrical engineering.
• They are also used in cryptography in encryption and decryption algorithms.

List of topics According to NCERT/JEE MAIN

Importance of Matrices Class 12

Matrices have a significant weighting in the IIT JEE test, which is a national level exam for 12th grade students that aids in admission to the country's top engineering universities. It is one of the most difficult exams in the country, and it has a significant impact on students' futures. Several students begin studying as early as Class 11 in order to pass this test. When it comes to math, the significance of these two chapters cannot be overstated due to their great weightage. You may begin and continue your studies with the standard books and these revision notes, which will ensure that you do not miss any crucial ideas and can be used to revise before any test or actual examination.

NCERT Notes Subject wise link:

• NCERT Notes for class 12 Physics.
• NCERT Notes for class 12 Chemistry.
• NCERT Notes for class 12 Mathematics.
• NCERT Notes for class 12 Biology

How to Study Matrices?

Start preparing by understanding and practicing the operations on matrices. Try to be clear on every types of matrices and their properties. Practice many problems from each topic for better understanding.

If you are preparing for competitive exams then solve as many problems as you can. Do not jump on the solution right away. Remember if your basics are clear you should be able to solve any question on this topic.

Important Books for Matrices

Start from NCERT Books, the illustration is simple and lucid. You should be able to understand most of the things. Solve all problems (including miscellaneous problem) of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the book Arihant Algebra Textbook by SK Goyal or Cengage Algebra Textbook by G. Tewani but make sure you follow any one of these not all. Matrices are explained very well in these books and there are an ample amount of questions with crystal clear concepts. Choice of reference book depends on person to person, find the book that best suits you the best, depending on how well you are clear with the concepts and the difficulty of the questions you require.

NCERT Solutions Subject wise link:

• NCERT solutions for class 12 Physics.
• NCERT solutions for class 12 Chemistry.
• NCERT solutions for class 12 Mathematics.
• NCERT solutions for class 12 Biology.

NCERT Exemplar Solutions Subject wise link:

• NCERT exemplar solutions for class 12 Physics.
• NCERT exemplar solutions for class 12 Chemistry.
• NCERT exemplar solutions for class 12 Mathematics.
• NCERT exemplar solutions for class 12 Biology.