Matrix Multiplication

In linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. In real life, we use matrices in solving linear systems of equations, and image processing.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

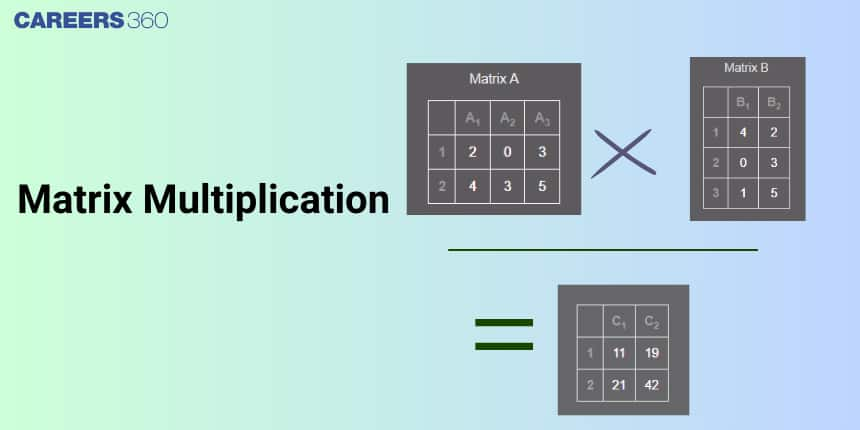
In this article, we will cover the concept of Matrix Multiplication. This category falls under the broader category of Matrices, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main Exam (from 2013 to 2023), a total of 44 questions have been asked on this concept, including five in 2019, three in 2020, eleven in 2021, nine in 2022, nine in 2023

Matrix multiplication Definition

A single matrix is produced by matrix multiplication, which is also referred to as matrix product and the multiplication of two matrices. This particular operation is binary.

The product of the two matrices $A$ and $B$, if they are $A$ and $B$, is represented as follows:

$X=A B$

As a result, the two matrices' product equals their dot product.

Matrix Multiplication by scalar

Let $\mathrm{k}$ be any scalar number, and $A=\left[a_{i j}\right]_{m \times n}$ be a matrix. Then the matrix is obtained by multiplying every element $\mathrm{A}$ by a scalar $\mathrm{k}$ and denoted as $\mathrm{kA}$.
$
\begin{aligned}
& k A=\left[k a_{i j}\right]_{m \times n} \\
& \qquad \mathrm{~A}=\left[\begin{array}{ll}
2 & 6 \\
3 & 7 \\
5 & 8
\end{array}\right] \text { then, } 3 \mathrm{~A}=\left[\begin{array}{ll}
3 \times 2 & 3 \times 6 \\
3 \times 3 & 3 \times 7 \\
3 \times 5 & 3 \times 8
\end{array}\right]=\left[\begin{array}{cc}
6 & 18 \\
9 & 21 \\
15 & 24
\end{array}\right]
\end{aligned}
$

Properties of scalar multiplication:

If $A$ and $B$ are two matrices and $k, l$ are scalar then
i) $k(A+B)=k A+k B$
ii) $k(A)=k(I A)=l(k A)$
iii) $(k+1) A=k A+1 A$
iv) $(-k) A=-(k A)=k(-A)$
v) $1 \mathrm{~A}=\mathrm{A},(-1) \mathrm{A}=-\mathrm{A}$

Note: $A$ and $B$ have the same order $m \times n$.

Matrix multiplication

Product $A B$ can be found if the number of columns in matrix $A$ and the number of rows in matrix $B$ are equal. Otherwise, multiplication $A B$ is not possible.
i) $A B$ is defined only if $\operatorname{col}(A)=\operatorname{row}(B)$
ii) $B A$ is defined only if $\operatorname{col}(B)=\operatorname{row}(A)$

If

$\begin{aligned} & \mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \\ & B=\left[b_{i j}\right]_{\mathrm{n} \times \mathrm{p}} \\ & \mathrm{C}=\mathrm{AB}=\left[\mathrm{c}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{p}} \\ & \text { Where } c_{i j}=\sum_{j=1}^n a_{i j} b_{j k}, 1 \leq \mathrm{i} \leq \mathrm{m}, 1 \leq \mathrm{k} \leq \mathrm{p} \\ & =\mathrm{a}_{\mathrm{i} 1} \mathrm{~b}_{1 \mathrm{k}}+\mathrm{a}_{\mathrm{i} 2} \mathrm{~b}_{2 \mathrm{k}}+\mathrm{a}_{\mathrm{i} 3} \mathrm{~b}_{3 \mathrm{k}}+\ldots+\mathrm{a}_{\mathrm{in}} \mathrm{b}_{\mathrm{nk}} \\ & \end{aligned}$

For example:

Suppose, two matrices are given
$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{33}
\end{array}\right]_{2 \times 3} \quad \text { and } \quad \mathrm{B}=\left[\begin{array}{lll}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} & b_{32} & b_{33}
\end{array}\right]_{3 \times 3}
$

To obtain the entries in row $i$ and column j of AB, we multiply the entries in row $i$ of $\mathrm{A}$ by column $j$ in $\mathrm{B}$ and add.
given matrices $\mathrm{A}$ and $\mathrm{B}$, where the order of $\mathrm{A}$ are $2 \times 3$ and the order of $\mathrm{B}$ are $3 \times 3$, the product of $\mathrm{AB}$ will be a $2 \times 3$ matrix.To obtain the entry in row 1, column 1 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the first column in $\mathrm{B}$, and add.

$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{11} \\
b_{21} \\
b_{31}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{11}+\mathrm{a}_{12} \cdot \mathrm{b}_{21}+\mathrm{a}_{13} \cdot \mathrm{b}_{31}
$

To obtain the entry in row 1, column 2 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the second column in B and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{12} \\
b_{22} \\
b_{32}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{12}+\mathrm{a}_{12} \cdot \mathrm{b}_{22}+\mathrm{a}_{13} \cdot \mathrm{b}_{32}
$

To obtain the entry in row 1, column 3 of $\mathrm{AB}$, multiply the first row in $A$ by the third column in B, and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{13} \\
b_{23} \\
b_{33}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{13}+\mathrm{a}_{12} \cdot \mathrm{b}_{23}+\mathrm{a}_{13} \cdot \mathrm{b}_{33}
$

We proceed the same way to obtain the second row of $\mathrm{AB}$. In other words, row 2 of $\mathrm{A}$ times column 1 of $\mathrm{B}$; row 2 of A times column 2 of B; row 2 of A times column 3 of B.

When complete, the product matrix will be
$
\mathrm{AB}=\left[\begin{array}{lll}
a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31} & a_{11} \cdot b_{12}+a_{12} \cdot b_{22}+a_{13} \cdot b_{32} & a_{11} \cdot b_{13}+a_{12} \cdot b_{23}+a_{13} \cdot b_{33} \\
a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31} & a_{21} \cdot b_{12}+a_{22} \cdot b_{22}+a_{23} \cdot b_{32} & a_{21} \cdot b_{13}+a_{22} \cdot b_{23}+a_{23} \cdot b_{33}
\end{array}\right]
$

Matrix multiplication rules

The following matrix multiplication rules and properties can be expressed using the above-described formula and process.

• If the number of rows in B equals the number of columns in A, then the product of two matrices A and B is defined.
• BA does not need to be defined if AB is defined.
• Both AB and BA are defined if A and B are square matrices of the same order.
• It is not required for AB to equal BA if both AB and BA are defined.
• One of the matrices is not required to be a zero matrix in order for the product of two matrices to be a zero matrix.

Properties of matrix multiplication:

i) Multiplication may or may not be commutative, so AB may or may not be equal to $BA$
ii) Matrix multiplication is associative, meaning $A(B C)=(A B) C$
iii) Matrix multiplication is distributive over addition, mean $A(B+C)=A B+A C$ and $(B+C) A=B A+C A$
iv) If matrix multiplication of two matrices gives a null matrix then it doesn't mean that any of those two matrices was a null matrix.

$A=\left[\begin{array}{ll}0 & 2 \\ 0 & 0\end{array}\right]$ and $B=\left[\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right]$, then $A B=\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$

v) Cancellation law in matrix multiplication doesn't hold, which means $A B=A C \Rightarrow B$ $=\mathrm{C}$
vi) Matrix multiplication $A \times A$ is represented by $A^2$. Thus, $A \cdot A \cdot A \cdot A$ .........$n$ times $=A^n$.

vii) if $\mathrm{A}$ is $\mathrm{m} \times \mathrm{n}$ matrix then, $\mathrm{I}_{\mathrm{m}} \mathrm{A}=\mathrm{A}=\mathrm{AI}_{\mathrm{n}}$.

Solved Example based on Multiplication of matrices

Example 1: Let $\mathrm{A}=\left[\mathrm{a}_{i j}\right]$ be a square matrix of order 3 such that $\mathrm{a}_{i j}=2^{j-i}$, for all $i, j=1,2,3$. Then, the matrix $\mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}$ is equal to: [JEE-2022]
Solution
Forming matrix A using the given $\mathrm{A}=\left[\mathrm{a}_{i j}\right]$ formula
$
\begin{aligned}
& \mathrm{A}=\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right] \\
& \mathrm{A}^2=\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 2^2 \\
2^{-1} & 1 & 2 \\
2^{-2} & 2^{-1} & 1
\end{array}\right] \\
& =\left[\begin{array}{ccc}
3 & 6 & 12 \\
3 \cdot 2^{-1} & 3 & 6 \\
3 \cdot 2^{-2} & 3 \cdot 2^{-1} & 3
\end{array}\right]=3 \mathrm{~A}
\end{aligned}
$

$
\begin{aligned}
& \therefore \mathrm{A}^2=3 \mathrm{~A} \\
& \Rightarrow \mathrm{A}^3=\mathrm{A}^2 \cdot \mathrm{A}=3 \mathrm{~A} \cdot \mathrm{A}=3 \mathrm{~A}^2=3 \cdot 3 \mathrm{~A}=3^2 \mathrm{~A} \\
& \Rightarrow \mathrm{A}^4=\mathrm{A}^2 \cdot \mathrm{A}^2=3 \mathrm{~A} \cdot 3 \mathrm{~A}=3^2 \mathrm{~A}^2=3^2 \cdot 3 \mathrm{~A}=3^3 \mathrm{~A}
\end{aligned}
$

Similarly $\mathrm{A}^5=3^4 \mathrm{~A}, \cdots \cdot \mathrm{A}^{10}=3^9 \mathrm{~A}$
$
\begin{aligned}
& \therefore \mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}=\mathrm{A}\left(3+3^2+\cdots+3^9\right) \\
& =\frac{3\left(3^9-1\right)}{3-1} \mathrm{~A} \\
& =\left(\frac{3^{10}-3}{2}\right) \mathrm{A} \text {. } \\
&
\end{aligned}
$

Hence, the matrix $\mathrm{A}^2+\mathrm{A}^3+\ldots+\mathrm{A}^{10}$ is equal to $=\left(\frac{3^{10}-3}{2}\right) \mathrm{A}$.

Example 2: Let $\mathrm{M}=\left[\begin{array}{cc}0 & -\alpha \\ \alpha & 0\end{array}\right]$, where $\alpha$ is a non-zero real number and $N=\sum_{k=1}^{49} \mathrm{M}^{2 \mathrm{k}}$. If $\left(\mathrm{I}-\mathrm{M}^2\right) \mathrm{N}=-2 \mathrm{I}$, then the positive integral value of $\alpha$ is [JEE-2022]

Solution
$
\begin{aligned}
& \mathrm{M}=\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right] \\
& \mathrm{M}^2=\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right]\left[\begin{array}{cc}
0 & -\alpha \\
\alpha & 0
\end{array}\right] \\
&=\left[\begin{array}{cc}
-\alpha^2 & 0 \\
0 & -\alpha^2
\end{array}\right] \\
&=-\alpha^2 \cdot \mathrm{I} \\
& \therefore \mathrm{M}^4=\mathrm{M}^2 \cdot \mathrm{M}^2=\alpha^4 \mathrm{I} \\
& \mathrm{M}^6=\mathrm{M}^4 \cdot \mathrm{M}^2=-\alpha^6 \mathrm{I} \\
&\ldots . . \\
&\ldots . . \\
& \therefore \mathrm{N}=\mathrm{M}^2+\mathrm{M}^4+\mathrm{M}^6+--+\mathrm{M}^{98}
\end{aligned}
$

$
\begin{aligned}
& =-\alpha^2 \mathrm{I}+\alpha^4 \mathrm{I}-\alpha^6 \mathrm{I} \ldots . .49 \text { terms } \\
& =\left(-\alpha^2+\alpha^4-\alpha^6-\ldots\right) \mathrm{I} \\
& =-\alpha^2\left(\frac{\left(-\alpha^2\right)^{49}-1}{-\alpha^2-1}\right) \mathrm{I}
\end{aligned}
$
$
\begin{aligned}
& \text { Given }\left(\mathrm{I}-\mathrm{M}^2\right) \mathrm{N}=-2 \mathrm{I} \\
& \Rightarrow\left(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{cc}
-\alpha^2 & 0 \\
0 & -\alpha^2
\end{array}\right]\right)\left(\frac{\alpha^2\left(-\alpha^{98}-1\right)}{\left(\alpha^2+1\right)}\right) \mathrm{I}=-2 \mathrm{I} \\
& \Rightarrow\left(1+\alpha^2\right) \mathrm{I} \cdot \frac{\alpha^2\left(-\alpha^{98}-1\right)}{\left(\alpha^2+1\right)}=-2 \mathrm{I} .
\end{aligned}
$

Only $\alpha=1$ satisfies it.
$
\Rightarrow \quad \alpha^2\left(-\alpha^{98}-1\right)=-2
$

Hence, the positive integral value of $\alpha$ is 1

Example 3: Let $\mathrm{A}=\left[\begin{array}{cc}1 & -1 \\ 2 & \alpha\end{array}\right]$ and $\mathrm{B}=\left[\begin{array}{ll}\beta & 1 \\ 1 & 0\end{array}\right], \alpha, \beta \in \mathbf{R}. {\text { Let } \alpha_1 \text { be the value of } \alpha \text { which satisfies }}(\mathrm{A}+\mathrm{B})^2=\mathrm{A}^2+\left[\begin{array}{ll}2 & 2 \\ 2 & 2\end{array}\right]$ and $\alpha_2$ be the value of $\alpha$ which satisfies $(\mathrm{A}+\mathrm{B})^2=\mathrm{B}^2$. Then $\left|\alpha_1-\alpha_2\right|_{\text {is equal }}$ to $\qquad$ [JEE-2022]

Solution

$\begin{aligned} & \mathrm{A}^2=\left[\begin{array}{cc}1 & -1 \\ 2 & \alpha\end{array}\right]\left[\begin{array}{ll}1 & -1 \\ 2 & 2\end{array}\right] \\ & \therefore\left[\begin{array}{cc}1 & -\alpha+1 \\ 2 \alpha+4 & \alpha^2\end{array}\right]=\left[\begin{array}{cc}(\beta+1)^2 & 0 \\ 3(\alpha+\beta+1) & \alpha^2\end{array}\right] \\ & \alpha=1=\alpha_1 \\ & \beta^2=\left[\begin{array}{ll}\beta & 1 \\ 1 & 0\end{array}\right]\left[\begin{array}{ll}\beta & 1 \\ 1 & \theta\end{array}\right] \\ & =\left[\begin{array}{ll}\beta^2+1 & \beta \\ \beta & 1\end{array}\right]=\left[\begin{array}{ll}(\beta+1)^2 & 0 \\ 3(\beta+1)+3 \alpha & \alpha^2\end{array}\right] \\ & \therefore \beta=0, \alpha=-1 \div \alpha_2 \\ & \left|\alpha_1-\alpha_2\right|=|1-(-1)|=2\end{aligned}$

Hence, the answer is 2.

Example 4: Let where $\mathrm{i}=\sqrt{-1}$. Then, the number of elements in the set $\left\{\mathrm{n} \in\{1,2, \ldots, 100\}: \mathrm{A}^{\mathrm{n}}=\mathrm{A}\right\}$ is [JEE-2017]
Solution:
$
\begin{aligned}
& A^2=\left[\begin{array}{cc}
1+i & 1 \\
-i & 0
\end{array}\right]\left[\begin{array}{cc}
1+i & 1 \\
-i & 0
\end{array}\right] \\
& =\left[\begin{array}{cc}
(1+i)^2-i & 1+i \\
-i+1 & -i
\end{array}\right] \\
& =\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right] \\
& \mathrm{A}^4=\mathrm{A}^2 \cdot \mathrm{A}^2 \\
& =\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right]\left[\begin{array}{cc}
i & 1+i \\
1-i & -i
\end{array}\right] \\
& =\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]=I \\
& \therefore \mathrm{A}^4=\mathrm{I} . \\
& \Rightarrow \mathrm{A}^{4 \mathrm{p}+1}=\left(\mathrm{A}^4\right)^{\mathrm{p}} \cdot \mathrm{A}=\mathrm{I} \cdot \mathrm{A}=\mathrm{A}
\end{aligned}
$
$\therefore \mathrm{n}$ should be of type $4 \mathrm{p}+1$

$
\mathrm{n}=1,5,9, \ldots, 97
$

Hence, the number of elements in the set $\left\{\mathrm{n} \in\{1,2, \ldots, 100\}: \mathrm{A}^{\mathrm{n}}=\mathrm{A}\right\}$ is 25 .

Example 5: Let $\mathrm{A}=\left[\begin{array}{lll}1 & a & a \\ 0 & 1 & b \\ 0 & 0 & 1\end{array}\right], \mathrm{a}, \mathrm{b} \in \mathbb{R}$. If for some $\mathrm{n} \in N, A^n=\left[\begin{array}{ccc}1 & 48 & 2160 \\ 0 & 1 & 96 \\ 0 & 0 & 1\end{array}\right]$ then $\mathrm{n}+\mathrm{a}+\mathrm{b}$ is equal to [JEE-2022]

Solution:

$
\begin{aligned}
& \mathrm{A}=\left[\begin{array}{lll}
1 & a & a \\
0 & 1 & b \\
0 & 0 & 1
\end{array}\right] \\
& =\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]+\left[\begin{array}{lll}
0 & a & a \\
0 & 0 & b \\
0 & 0 & 0
\end{array}\right] \\
& =\mathrm{I}+\mathrm{B} \text { (let) } \\
&
\end{aligned}
$
where $\mathrm{B}=\left[\begin{array}{lll}0 & a & a \\ 0 & 0 & b \\ 0 & 0 & 0\end{array}\right]$
Now $B^2=\left[\begin{array}{ccc}0 & 0 & a b \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$
and $\mathrm{B}^3=0$
So $\mathrm{A}^{\mathrm{n}}=(\mathrm{I}+\mathrm{B})^{\mathrm{n}}$
$
=\mathrm{I}^{\mathrm{n}}+{ }^{\mathrm{n}} \mathrm{C}_1 \cdot \mathrm{B}+{ }^{\mathrm{n}} \mathrm{C}_2 \cdot \mathrm{B}^2+0+0+\cdots
$

$
\begin{aligned}
& =\mathrm{I}+\mathrm{n}\left[\begin{array}{lll}
0 & a & a \\
0 & 0 & b \\
0 & 0 & 0
\end{array}\right]+\frac{\mathrm{n}(\mathrm{n}-1)}{2} \\
& =\left[\begin{array}{ccc}
0 & 0 & a b \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right] \\
& =\left[\begin{array}{ccc}
1 & n a & n a+\frac{n(n-1)}{2} a b \\
0 & 1 & n b \\
0 & 0 & 1
\end{array}\right]
\end{aligned}
$

Comparing with the given matrix
$
\begin{aligned}
& \mathrm{na}=48, \mathrm{nb}=96, \frac{\mathrm{n}(\mathrm{n}-1)}{2} \mathrm{ab}=2112 \\
& \Rightarrow \mathrm{a}=4, \mathrm{~b}=8, \mathrm{n}=12 \\
& \therefore \mathrm{n}+\mathrm{a}+\mathrm{b}=24
\end{aligned}
$

Hence, the value of $n+a+b$ is 24.