Maxima and Minima in Calculus

Functions are one of the basic concepts in mathematics that have numerous applications in the real world. Be it mega skyscrapers or super-fast cars, their modeling requires methodical application of functions. Almost all real-world problems are formulated, interpreted, and solved using functions. Image and pre-image help in determining the domain and range of the function. The practical applications of image and pre-image are graphing functions, inverse functions, and database queries.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Maxima and Minima of a Function
2. Methods to find points of Local maxima and Local minima
3. Solved Examples Based on Maxima and Minima of Function:
4. Summary

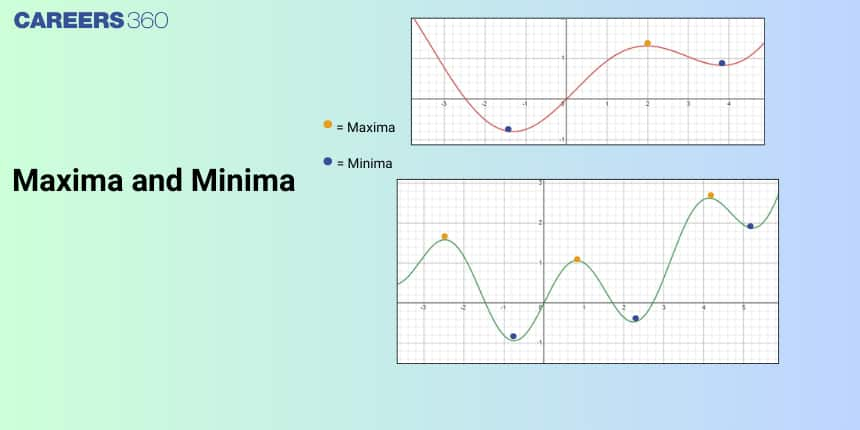
In this article, we will cover the concepts of Maxima and Minima of the function. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of thirty-nine questions have been asked on this concept, including two in 2013, two in 2015, four in 2016, one in 2017, two in 2018, five in 2019, four in 2020, eight in 2021, six in 2022, and three in 2023.

Maxima and Minima of a Function

Function-

A relation from a set $A$ to a set $B$ is said to be a function from $A$ to $B$ if every element of set $A$ has one and only one image in set $B$.

OR
$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as
$f: A \rightarrow B$ and read as $f$ is a mapping from $A$ to $B$.
Let $f$ be a function defined on an open interval $I$. Let $f$ be continuous at a critical point $c$ in $I$. Then
(i) If $f^{\prime}(x)$ changes sign from positive to negative as $x$ increases through $c$, i.e., if $f^{\prime}(x)>0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)<0$ at every point sufficiently close to and to the right of $c$ , then $c$ is a point of local maxima.
(ii) If $f^{\prime}(x)$ changes sign from negative to positive as $x$ increases through $c$, i.e., if $f^{\prime}(x)<0$ at every point sufficiently close to and to the left of $c$, and $f^{\prime}(x)>0$ at every point sufficiently close to and to the right of $c$ , then $c$ is a point of local minima.

Let $y=f(x)$ be a real function defined at $x=a$. Then the function $f(x)$ is said to have a maximum value at $x=a$ if $f(x) \leq f(a) \quad \forall a \in$ R .

And also the function $f(x)$ is said to have a minimum value at $x=$ a, if $f(x) \geq f(a) \quad \forall a \in R$

Concept of Local Maxima and Local Minima

The function $f(x)$ is said to have a local maxima (or maxima) at a point ' $a$ ' if the value of $f(x)$ at ' $a$ ' is greater than its values for all $x$ in a small neighborhood of ' $a$ ' .

In other words, $f(x)$ has a maxima at $x=$ ' $a$ ', if $f(a+h) \leq f(a)$ and $f(a-h) \leq f(a)$, where $h>0$ (very small quantity).

The function $f(x)$ is said to have local minima (or minima) at a point '$b$' if the value of $f(x)$ at ' $b$ ' is less than its values for all $x$ in a small neighborhood of $'b'$ .

In other words, $f(x)$ has a maximum at $x=$ ' $b$ ', if $f(b+h) \geq f(b)$ and $f(b-h) \geq f(b)$, where $h>0$ (very small quantity).

Methods to find points of Local maxima and Local minima

At points of local maxima and local minima, the slope of the tangent drawn to the curve is zero. For local maximum $\frac{d y}{d x}$ changes from positive to negative and for local minimum $\frac{d y}{d x}$ changes from negative to positive.

Where $y=f(x)$

$
\frac{d y}{d x}=f^{\prime}(x)
$

By second derivative method :
Step 1. find values of $x$ for $\frac{d y}{d x}=0$
Step 2. $x=x_{\circ}$ is a point of local maximum if $f^{\prime \prime}(x)<0$ and local minimum if $f^{\prime \prime}(x)>0$.

Recommended Video Based on Maxima and Minima of Function:

Solved Examples Based on Maxima and Minima of Function:

Example 1: Let the tangents drawn to the circle, $x^2+y^2=16$ from the point $P(0, h)$ meet the $x$-axis at points $A$ and $B$. If the area of $\triangle A P B$ is minimum, then h is equal to :
[JEE Main 2015]
1) $4 \sqrt{3}$
2) $3 \sqrt{3}$
3) $3 \sqrt{2}$
4) $4 \sqrt{2}$

Solution

As we learned in

Maxima Minima -

A functions graph follows up and down along the x-axis then the upper part is known as maxima and lower part is known as minima.

-

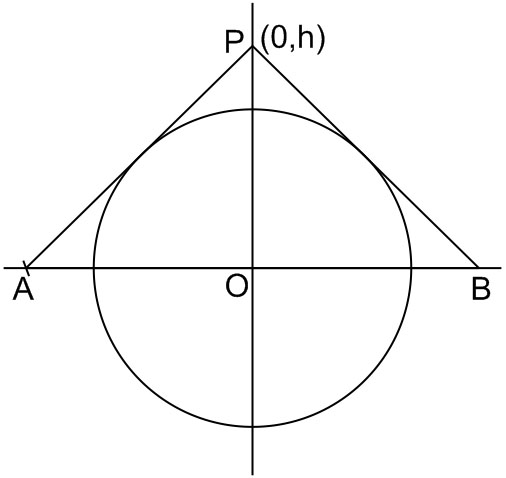
Let equation of tangent is

$
\begin{aligned}
& (y-h)=M(x-0) \\
& \therefore y=M x-h \\
& \therefore h= \pm \sqrt{1+M^2} \\
& \therefore A B= \pm \frac{4 \sqrt{1+M^2}}{M} \\
& \therefore \text { Area }=\frac{1}{2} \times A B \times O P \\
& =\frac{1}{2} \times \frac{8 \sqrt{1+M^2}}{M} \times 4 \sqrt{1+M^2} \\
& \frac{d A}{d m}=0 \\
& \therefore h=4 \sqrt{1+1}=4 \sqrt{2}
\end{aligned}
$

Example 2: If $f(x)$ is non-zero polynomial of degree four,having local extreme points at $x=-1,0,1$; then the set $S=\{x \in R: f(x)=f(0)\}$ contains exactly : [JEE Main 2019]

1) four irrational numbers.

2) four rational numbers.

3) two irrational and two rational numbers.

4) two irrational and one rational number.

Solution

given that
$
\begin{aligned}
& f(x)=f(0) \\
& a\left(\frac{x^4}{4}-\frac{x^2}{2}\right)+c=c \\
& \left(\frac{x^4}{4}-\frac{x^2}{2}\right)=0 \\
& \Rightarrow x^2\left(x^2-2\right)=0 \\
& x=0, \pm \sqrt{2} \\
& S=\{0, \sqrt{2},-\sqrt{2}\}
\end{aligned}
$

Example 3: The maximum volume (in cu.m) of the right circular cone having a slant height $3$m is: [JEE Main 2019]
1) $6 \pi$
2) $3 \sqrt{3} \pi$
3) $\frac{4}{3} \pi$
4) $2 \sqrt{3} \pi$

Solution

Method for maxima or minima -

By second derivative method :

Step 1. find values of $x$ for $\frac{d y}{d x}=0$
Step 2. $x=x_{\circ}$ is a point of local maximum if $f^{\prime \prime}(x)<0$ and local minimum if $f^{\prime \prime}(x)>0$
- wherein

Where $y=f(x)$

$
\frac{d y}{d x}=f^{\prime}(x)
$

$
\begin{aligned}
& l=3 m(\text { slant height }) \\
& h=3 \cos (\theta) \\
& r=3 \sin (\theta)
\end{aligned}
$

Volume of right circular cone

$
\begin{aligned}
V & =\frac{1}{3} \pi r^2 h \\
& =\frac{1}{3} \pi(3 \sin (\theta))^2(3 \cos (\theta)) \\
V & =\frac{\pi}{3} 9 \sin ^2 \theta \cdot 3 \cos (\theta)=9 \pi \sin ^2 \theta \cdot \cos \theta
\end{aligned}
$

for maximum volume

$
\begin{aligned}
& \frac{\mathrm{dv}}{\mathrm{d} \theta}=0, \quad \frac{\mathrm{d} v}{\mathrm{~d} \theta}=-9 \pi \sin (\theta)\left[\sin ^2(\theta)-2 \cos ^2(\theta)\right]=0 \\
& \sin (\theta)=\sqrt{\frac{2}{3}}
\end{aligned}
$

$
\frac{\mathrm{d}^2 v}{\mathrm{~d} \theta^2}=- \text { ve at } \sin (\theta)=\sqrt{\frac{2}{3}}
$

Volume is maximum when

$
\begin{aligned}
& \text { Volume is maximum when } \sin (\theta)=\sqrt{\frac{2}{3}} \\
& \therefore V_{\text {max }}=2 \sqrt{3} \pi(\text { cu.m })
\end{aligned}
$

Example 4: If $p(x)$ is a polynomial of degree three that has a local maximum value 8 at $x=1$ and a local minimum value $4$ at $x=2$; then $p(0)$ is equal to:
[JEE Main 2020]
1) $6$
2) $-12$
3) $-24$
4) $12$

Solution

Since $p(x)$ has relative extreme at $x=1 \& 2$

$
\begin{aligned}
& \text { so } \mathrm{p}^{\prime}(\mathrm{x})=0 \text { at } \mathrm{x}=1 \& 2 \\
& \Rightarrow \mathrm{p}^{\prime}(\mathrm{x})=\mathrm{A}(\mathrm{x}-1)(\mathrm{x}-2) \\
& \Rightarrow p(x)=\int A\left(x^2-3 x+2\right) d x \\
& p(x)=A\left(\frac{x^3}{3}-3 x^2+2 x\right)+C \\
& \mathrm{P}(1)=8
\end{aligned}
$

from (1)

$
\begin{aligned}
& 8=A\left(\frac{1}{3}-\frac{3}{2}+2\right)+C \\
& \Rightarrow 8=\frac{5 \mathrm{~A}}{6}+\mathrm{C} \Rightarrow 48=5 \mathrm{~A}+5 \mathrm{C} \\
& \mathrm{P}(2)=4 \\
& \Rightarrow 4=\mathrm{A}\left(\frac{8}{3}-6+4\right)+\mathrm{C} \\
& \Rightarrow 4=\frac{2 \mathrm{~A}}{3}+\mathrm{C} \Rightarrow 12=2 \mathrm{~A}+3 \mathrm{C}
\end{aligned}
$

From above

$
C=-12 \text { So } P(0)=C=-12
$

Example 5: If a rectangle is inscribed in an equilateral triangle of side length $2 \sqrt{2}$ as shown in the figure, then the square of the largest area of such a rectangle is $\qquad$ [JEE Main 2021]

1) $3$

2) $1$

3) $4$

4) $6$

Key Concepts

Solution

Let height of rectangle $=\mathrm{x}$

$
\frac{x}{y}=\tan 60^{\circ} \Rightarrow y=\frac{x}{\sqrt{3}}
$

$\therefore$ Length of rectangle $=2 \sqrt{2}-2 y=2 \sqrt{2}-\frac{2 x}{\sqrt{3}}$
Area of rectangle $=x\left(2 \sqrt{2}-\frac{2 x}{\sqrt{3}}\right)$

$
=2 \sqrt{2} x-\frac{2}{\sqrt{3}} x^2
$

For max area $\Rightarrow 2 \sqrt{2}-\frac{4}{\sqrt{3}} x=0\left(f^{\prime}(x)=0\right)$

$
\begin{gathered}
\Rightarrow x=\sqrt{\frac{3}{2}} \\
\text { Area }=2 \sqrt{2} \sqrt{\frac{3}{2}}-\frac{2}{\sqrt{3}} \frac{3}{2}=2 \sqrt{3}-\sqrt{3}=\sqrt{3}
\end{gathered}
$

Square of Area $=3$

Summary

The Maxima and minima of a function are critical points where the function reaches its highest and lowest values within a given range. We concluded that function is a very important term in mathematics. Without this half of the mathematics is meaningless. With the concepts of maxima and minima, one can gain a deeper understanding of the behavior of functions and their mappings between different sets.