Maximum and Minimum value of Trigonometric Function

Trigonometric functions are fundamental in mathematics, particularly in geometry, calculus, and applied mathematics. They are used to describe relationships involving lengths and angles in right triangles. The graph of trigonometric functions helps in finding the domain and its range with the help of maximum and minimum values. The six basic trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent are the trigonometric functions.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

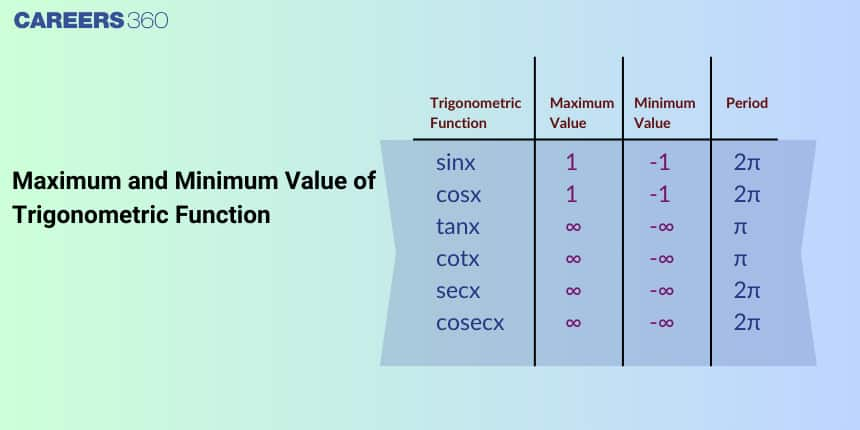
Maximum and Minimum Value of Trigonometric Function

In trigonometry, there are six basic trigonometric functions. These functions are trigonometric ratios that are based on ratios of sides in a right triangle: the hypotenuse (the longest side), the base (the side adjacent to a chosen angle), and the perpendicular (the side opposite the chosen angle). These functions are sine, cosine, tangent, secant, cosecant, and cotangent. They help us find different values in triangles by comparing these side lengths.

The basic formulas to find the trigonometric functions are as follows:

• $\sin \theta=$ Perpendicular/Hypotenuse
• $\cos \theta=$ Base/Hypotenuse
• $\tan \theta=$ Perpendicular/Base
• $\sec \theta=$ Hypotenuse/Base
• $\operatorname{cosec} \theta=$ Hypotenuse/Perpendicular
• $\cot \theta=$ Base/Perpendicular

The trigonometric functions' domain θ can be represented in either degrees or radians. A table showing some of the principal values of θ for the different trigonometric functions can be seen below. These principal values, usually referred to as standard values of the trig function at specific angles, are frequently used in computations. The principal values of trigonometric functions have been found from a unit circle.

We know that range of $\sin x$ and $\cos x$ which is $[-1,1]$,

If there is a trigonometric function in the form of a $\sin x+b \cos x$, then replace a with $r \cos \theta$ and $b$ with $r \sin \theta$.

Then we have,

$
\begin{aligned}
a \sin \mathrm{x}+b \cos \mathrm{x} & =r \cos \theta \sin \mathrm{x}+r \sin \theta \cos \mathrm{x} \\
& =r(\cos \theta \sin \mathrm{x}+\sin \theta \cos \mathrm{x}) \\
& =r \sin (\mathrm{x}+\theta)
\end{aligned}
$

where $r=\sqrt{a^2+b^2}$ and, $\tan \theta=\frac{\mathrm{b}}{\mathrm{a}}$

$
\begin{aligned}
& \text { Since, }-1 \leq \sin (\mathrm{x}+\theta) \leq 1 \\
& \text { Multiply with }{ }^{\prime} \mathrm{r}^{\prime} \\
& \Rightarrow-\mathrm{r} \leq \mathrm{r} \sin (\mathrm{x}+\theta) \leq \mathrm{r} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \mathrm{r} \sin (\mathrm{x}+\theta) \leq \sqrt{a^2+b^2} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq a \sin \mathrm{x}+b \cos \mathrm{x} \leq \sqrt{a^2+b^2}
\end{aligned}
$

So, the minimum value of the trigonometric function $\mathrm{a} \sin \mathrm{x}+\mathrm{b} \cos \mathrm{x}$ is $-\sqrt{a^2+b^2}$ and maximum value is $\sqrt{a^2+b^2}$.

$\begin{array}{|c|c|c|c|c|c|c|}
\hline t \text {-function } & 0^{\circ} & 30^{\circ} \text { or } \frac{\pi}{3} & \mathbf{4 5} \text { or } \frac{\pi}{4} & \mathbf{6 0}{ }^{\circ} \text { or } \frac{\pi}{6} & 90^{\circ} \text { or } \frac{\pi}{2} & 180^{\circ} \text { or } \pi \\
\hline \sin \theta & 0 & \frac{1}{2} & \frac{1}{\sqrt{2}} & \frac{\sqrt{3}}{2} & 1 & 0 \\
\hline \cos \theta & 1 & \frac{\sqrt{3}}{2} & \frac{1}{\sqrt{2}} & \frac{1}{2} & 0 & -1 \\
\hline \tan \theta & 0 & \frac{1}{\sqrt{3}} & 1 & \sqrt{3} & \text { undefined } & 0 \\
\hline \operatorname{cosec} \theta & \text { undefined } & 2 & \sqrt{2} & \frac{2}{\sqrt{3}} & 1 & \text { undefined } \\
\hline \sec \theta & 1 & \frac{2}{\sqrt{3}} & \sqrt{2} & 2 & \text { undefined } & -1 \\
\hline \cot \theta & \text { undefined } & \sqrt{3} & 1 & \frac{1}{\sqrt{3}} & 0 & \text { undefined } \\
\hline
\end{array}$

Quadratic Equation

A quadratic equation is the equation of a second-degree polynomial where it has a minimum of one term which is a higher degree 2. It is one of the types of a polynomial function. In this quadratic equation, the constant ‘a’ cannot be zero. The general form of the quadratic equation is given below:

$ax^2 + bx+c$

Maximum and Minimum Value of Quadratic Equation Formula

The maximum and minimum values of the quadratic equation will be determined with the help of the quadratic formula, which is given below:

$
\begin{gathered}
D=b^2-4 a c \\
y=a x^2+b x+c \\
a x^2+b x+c-y=0
\end{gathered}
$

For finding the zeros of the above equation using the discriminant formula:

$
\begin{gathered}
b^2-4 a(c-y) \geq 0 \\
b^2-4 a c+4 a y \geq 0 \\
4 a y \geq 4 a c-b^2 \\
b^2-4 a(c-y) \geq 0 \\
b^2-4 a c+4 a y \geq 0 \\
4 a y \geq 4 a c-b^2
\end{gathered}
$

When $a>0$, using equation (1):

$
\begin{gathered}
4 a y \geq 4 a c-b^2 \\
y \geq \frac{4 a c-b^2}{4 a} \\
4 a y \geq 4 a c-b^2 \\
y \geq \frac{4 a c-b^2}{4 a}
\end{gathered}
$

It can be seen that whenever the value of constant $a$ is greater than zero, it will give the minimum value of $y$. Therefore, the minimum value of the quadratic equation is

$
\frac{4 a c-b^2}{4 a}
$

When $a<0$, using equation (1):

$
\begin{gathered}
4 a y \geq 4 a c-b^2 \\
y \leq \frac{4 a c-b^2}{4 a} \\
4 a y \geq 4 a c-b^2 \\
y \leq \frac{4 a c-b^2}{4 a}
\end{gathered}
$

It can be seen that whenever the value of constant $a$ is smaller than zero, it will give the maximum value of $y$. Therefore, the maximum value of the quadratic equation is

$
\frac{4 a c-b^2}{4 a}
$

Summary

Finding minimizing and maximizing helps to understand the basic functions of trigonometry, derivatives, etc. They are essential instruments in many scientific and engineering fields because of their qualities and uses, which go well beyond perfect triangles.

Solved Examples Based on Maximum and Minimum Value of Trigonometric Function

Example 1: What is the maximum value of the expression?

$
f(n)=5 \sin \left(x+\frac{\pi}{4}\right)+3 \cos \left(x+\frac{\pi}{4}\right)
$

1) 4
2) $4 \sqrt{2}$
3) $\sqrt{34}$
4) None of these

Solution

As we learned in the concept

Maximum and minimum values:
The maximum and minimum values of $a \cos \Theta+b \sin \Theta$

$
\begin{aligned}
& \text { Max. value }=\sqrt{a^2+b^2} \\
& f(n)=5\left(\frac{\sin x}{\sqrt{2}}+\frac{\cos x}{\sqrt{2}}\right)+3\left(\frac{\cos x}{\sqrt{2}}-\frac{\sin x}{\sqrt{2}}\right) \\
& =\sqrt{2} \sin x+4 \sqrt{2} \cos x \\
& \text { Max value }=\sqrt{\sqrt{2}^2+4 \sqrt{2}^2}=\sqrt{34}
\end{aligned}
$
Hence, the correct option is option 3.

Example 2: Find out the range of function $4 \sin x-\sin ^2 x-1$
1) $[-1,2]$
2) $[-1,4]$
3) $[-6,2]$
4) $[-6,1]$

Solution

Maximum and Minimum Value of Trigonometric Function

We know that range of $\sin \mathrm{x}$ and $\cos \mathrm{x}$ which is $[-1,1]$,
If there is a trigonometric function in the form of a $\sin \mathrm{x}+\mathrm{b} \cos \mathrm{x}$, then replace a with $\mathrm{r} \cos \theta$ and b with $\mathrm{r} \sin \theta$.

$
\begin{aligned}
a \sin \mathrm{x}+b \cos \mathrm{x} & =r \cos \theta \sin \mathrm{x}+r \sin \theta \cos \mathrm{x} \\
& =r(\cos \theta \sin \mathrm{x}+\sin \theta \cos \mathrm{x}) \\
& =r \sin (\mathrm{x}+\theta)
\end{aligned}
$
Then we have, where $r=\sqrt{a^2+b^2}$ and, $\tan \theta=\frac{\mathrm{b}}{\mathrm{a}}$

Since, $-1 \leq \sin (x+\theta) \leq 1$
Multiply with ' r '

$
\begin{aligned}
& \Rightarrow-\mathrm{r} \leq \sin (\mathrm{x}+\theta) \leq \mathrm{r} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \sin (\mathrm{x}+\theta) \leq \sqrt{a^2+b^2} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq a \sin \mathrm{x}+b \cos \mathrm{x} \leq \sqrt{a^2+b^2}
\end{aligned}
$

So, the minimum value of the trigonometric function $\mathrm{a} \sin \mathrm{x}+\mathrm{b} \cos \mathrm{x}$ is $-\sqrt{a^2+b^2}$ and the maximum value is $\sqrt{a^2+b^2}$.
$4 \sin x-\sin ^2 x-1=-(\sin x-2)^2+3$
Range of this function is $[-6,2]$
Hence, the answer is option 3.

Example 3: find the minimum value of $\sin 2 x+\csc 2 x \quad x \in\left[0, \frac{\pi}{2}\right]$
1) $-\infty$
2) -2
3) 2
4) 1

Solution

Maximum and Minimum Value of Trigonometric Function

We know that range of $\sin x$ and $\cos x$ which is $[-1,1]$

If there is a trigonometric function in the form of a $\sin x+b \cos x$, then replace a with $\mathrm{r} \cos \theta$ and b with $\mathrm{r} \sin \theta$.

$
\begin{aligned}
a \sin \mathrm{x}+b \cos \mathrm{x} & =r \cos \theta \sin \mathrm{x}+r \sin \theta \cos \mathrm{x} \\
& =r(\cos \theta \sin \mathrm{x}+\sin \theta \cos \mathrm{x}) \\
& =r \sin (\mathrm{x}+\theta)
\end{aligned}
$
Then we have, where $r=\sqrt{a^2+b^2}$ and, $\tan \theta=\frac{\mathrm{b}}{\mathrm{a}}$

$
\begin{aligned}
& \text { Since, }-1 \leq \sin (\mathrm{x}+\theta) \leq 1 \\
& \text { Multiply with }{ }^{\prime} \mathrm{r}^{\prime} \\
& \Rightarrow-\mathrm{r} \leq \sin (\mathrm{x}+\theta) \leq \mathrm{r} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \sin (\mathrm{x}+\theta) \leq \sqrt{a^2+b^2} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq a \sin \mathrm{x}+b \cos \mathrm{x} \leq \sqrt{a^2+b^2}
\end{aligned}
$

So, the minimum value of the trigonometric function $a \sin x+b \cos x$ is $-\sqrt{a^2+b^2}$ and the maximum value is $\sqrt{a^2+b^2}$.
we know $A \cdot M . \geq G . M$.

$
\frac{\sin 2 x+\csc 2 x}{2} \geq(\sin 2 x \cdot \csc 2 x)^{\frac{1}{2}}
$
$
\sin 2 x+\csc 2 x \geq 2
$

Hence, the answer is option 3.

Example 4: The number of integral values of ' $k$ ' for which the equation $3 \sin x+4 \cos x=k+1$ has a solution, $k \in R$ is $\qquad$

1) 10
2) 8
3) 11
4) 9

Solution

$
\begin{aligned}
& 3 \sin x+4 \cos x=k+1 \\
& \Rightarrow \mathrm{k}+1 \in\left[-\sqrt{3^2+4^2}, \sqrt{3^2+4^2}\right] \\
& \Rightarrow \mathrm{k}+1 \in[-5,5] \\
& \Rightarrow \mathrm{k} \in[-6,4]
\end{aligned}
$

No. of integral values of $\mathrm{k}=11$
Hence, the answer is the option 3.

Example 5 : What is the maximum value of the expression $-5 \sin (x+\pi / 4)-3 \cos (x+\pi / 4)$
1) 4
2) $4 \sqrt{2}$
3) $\sqrt{34}$
4) None of these

Solution
Let $x+\pi / 4=\theta$
So the expression is $-5 \sin \theta-3 \cos \theta$
Its maximum value is $=\sqrt{(-5)^2+(-3)^2}=\sqrt{34}$
Hence, the answer is the option (2).