One to One Function - Graph, Examples, Definition

A one-to-one function, also known as an injective function, is a function where each domain element is mapped to a unique element in the codomain. In other words, no two different elements in the domain map to the same element in the codomain. Understanding one-to-one functions is fundamental in various branches of mathematics, particularly in algebra and calculus.

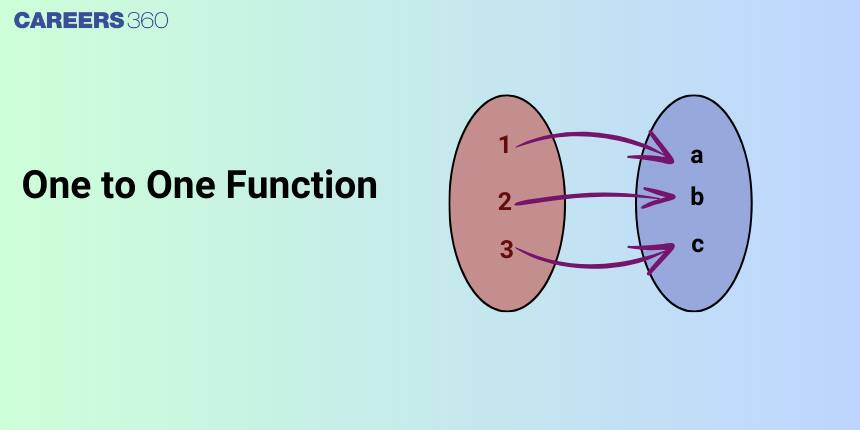
In this article, we will explore the concept of one-to-one functions, a key topic within the broader category of relations and functions. This concept is crucial for board exams and competitive exams like the Joint Entrance Examination (JEE Main), as well as other entrance tests such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the past decade (2013-2023) in the JEE Main exam, a total of six questions have addressed this concept, with one question in 2017, two in 2019, one in 2021, one in 2022, and one in 2023.

Function

A relation from a set $A$ to a set $B$ is said to be a function from $A$ to $B$ if every element of set $A$ has one and only one image in set $B$.

OR
$A$ and $B$ are two non-empty sets, so a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as
$f: A \rightarrow B$ and read as $f$ is mapping from $A$ to $B$.

Function Function Not a function

Not a function

Third one is not a function because d is not related(mapped) to any element in $B$.
Fourth is not a function as element a in $A$ is mapped to more than one element in $B$.

One-one function

An injective function, sometimes referred to as a one-to-one function, is one in which distinct elements of A have distinct relationships with B or distinct images with B. If a function has distinct images, it can only be one-to-one if the pre-images are different. Similarly, if the elements in B set differ, it can only be one-to-one if the elements in A set had different pre-images.

A function $f: X \rightarrow Y$ is called a one-one (or injective) function, if different elements of $X$ have different images in $B$. i.e. no two elements of set $X$ can have the same image.
Consider,
$f: X \longrightarrow Y$, function given by $y=f(x)=x$, and
$X=\{-2,2,4,6\}$ and $Y=\{-2,2,4,6\}$

Graphically it can be shown that for every x, there is a unique y (or no y has more than one x corresponding to it) as below and hence it is one-one.

Now, consider, $\mathrm{X}_1=\{1,2,3\}$ and $\mathrm{X}_2=\{\mathrm{x}, \mathrm{y}, \mathrm{z}\}$

$
\mathrm{f}: \mathrm{X}_1 \longrightarrow \mathrm{X}_2
$

Method to check One-One Function

1. If $x_1, x_2 \in x$, then $f\left(x_1\right)=f\left(x_2\right) \Rightarrow x_1=x_2$

2. A function is one-one if no line parallel to the X-axis meets the graph of the function at more than one point.

3. Even degree polynomials are NOT one-one functions

Example of One-to-One Functions

• Identity Function: The identity function is a simple example of a one-to-one function. It takes an input and returns the same value as the output. For any real number $x$, the identity function is defined as:

$f(x)=x$

Every distinct input x corresponds to a distinct output f(x), making it a one-to-one function.

• Linear Function: A linear function is one where the highest power of the variable is 1. For example:

$f(x)=2 x+3$

This is a one-to-one function because no matter what value of $x$ you choose, you will get a unique value for $f(x)$.

• Absolute Value Function: The absolute value function f(x)=∣x∣ is also a one-to-one function. For any real number x, the absolute value function returns a non-negative value, and different values of x will result in different absolute values.

Number of One-One Function

If A and B are finite sets having elements m and n respectively, then the number of one-one functions from A to B is

$=\left\{\begin{array}{cl}{ }^n P_m & \text { if } n \geq m \\ 0 & \text { if } n<m\end{array}\right.$

Properties of One-to-One Functions

1. Uniqueness: Each element of the domain maps to a unique element in the codomain.
2. Inverse Function: If f is a one-to-one function, then it has an inverse function $f^{-1}$, which is also a function.
3. Horizontal Line Test: A function $f$ is one-to-one if and only if no horizontal line intersects the graph of $f$ more than once.

Solved Examples Based On the One-One Functions

Example1: The function
$f: R \rightarrow\left[-\frac{1}{2}, \frac{1}{2}\right]_{\text {defined as }} f(x)=\frac{x}{1+x^2}$, is
1) injective but not surjective
2) surjective but not injective
3) neither injective nor surjective
4) invertible

Solution:

Solution:

$
\begin{aligned}
& f(x)=\frac{x}{1+x^2} \\
& f: R \rightarrow\left[-\frac{1}{2}, \frac{1}{2}\right] \\
& f^{\prime}(x)=\frac{\left(1+x^2\right) \times 1-x \times 2 x}{\left(1+x^2\right)^2}=\frac{1+x^2-2 x^2}{\left(1+x^2\right)^2}=\frac{1-x^2}{\left(1+x^2\right)^2} \\
& \therefore \text { So that } \frac{-\left(x^2-1\right)}{\left(x^2+1\right)^2}
\end{aligned}
$

So that it is not strictly increasing or decreasing function.
So that it is not one-one.
So, the given function is surjective but not injective.
Hence, the answer is the option 2.

Example 2: Which of the following functions are one - one functions?
1) $f(x)=x^2$
2) $f(x)=x^4$
3) $f(x)=\cos x$
4) $f(x)=\sqrt{x}$

Solution:
A line parallel to the $x$-axis cuts the curve of one-one function at at most one point.

$
f(x)=\sqrt{x}
$
Clearly, this function is one - one function.
Hence, the answer is the option (4).

Example 3: Which of the following functions are one-one functions?
1) $\sin (\cos x)$
2) $\cos (\sin x)$
3) $\sin (\tan x)$
4) None of these

Solution:
As we learned
In the case of composite functions,
If both $f(x)$ and $g(x)$ are one-one functions, then fog $(x)$ and $g \circ f(x)$ are both one-one functions.
Hence, the answer is the option 4 .

Example 4: Let $A=x \in \mathrm{R}: \mathrm{x}$ is not a positive integer. Define a function $f: A \rightarrow R_{\text {as }}$ $f(x)=\frac{2 x}{x-1}$ then f is:
1) injective but not surjective
2) neither injective nor surjective
3) not injective
4) surjective but not injective

Solution:
One - One or Injective function -
A function in which every element of the range of function corresponds to exactly one element.
- wherein

A line parallel to the $x$-axis cuts the curve at most one point.

$
f(x)=\frac{2 x}{x-1}
$
This can be written as

$
\begin{aligned}
f(x) & =2\left(1+\frac{1}{x-1}\right) \\
f^{\prime}(x) & =-\frac{2}{(x-1)^2}
\end{aligned}
$

$\Rightarrow \mathrm{f}$ is one-one i.e injective but not surjective.
Hence, the answer is option 1 .
Example 5: Which of the functions $\mathrm{f}(\mathrm{x})$ will be one-one functions if $f^{\prime}(x)$ is given
1) $f^{\prime}(x)=\sin x, x \equiv R$
2) $f^{\prime}(x)=e^x, x \equiv R$
3) $f^{\prime}(x)=\ln x, x \equiv R^{+}$
4) $f^{\prime}(x)=\cos x, x \equiv R$

Solution:

When $f^{\prime}=e^x>0$
Then $f(x)$ is an increasing function, so it is a one-one function.
Hence, the answer is option 2.

Summary

A one-to-one function is a critical concept in mathematics, ensuring that each input maps to a unique output. Recognizing and proving that a function is one-to-one allows for deeper analysis and application, including the determination of inverse functions and solving unique solutions to equations. Understanding and identifying one-to-one functions is foundational for advanced mathematical studies and various practical applications.

Frequently Asked Questions(FAQ)-

1. What is a function?

Ans: $A$ relation from a set $A$ to a set $B$ is said to be $a$ function from $A$ to $B$ if every element of $\operatorname{set} A$ has one and only one image in set $B$.
2. What is one-one function?

Ans: A function $\mathrm{f}: \mathrm{X} \rightarrow \mathrm{Y}$ is called a one-one (or injective) function, if different elements of X have different images in B. i.e. no two elements of set $X$ can have the same image.
3. What is the difference between one-one and many functions?

Ans: One-one function has a single value for the single domain but many-one function has multiple values for a single input.
4. Is degree polynomial a one-one function?

Ans: Degree polynomials may not be one-one function.
5. Give some examples of one-one function.

Ans: Logarithmic function, constant function, odd degree polynomial, etc are some one-one functions.