Product To Sum Formulas

The Product to sum formulas in trigonometry are formulas that are used to express the product of sine and cosine functions into the sum and difference of sine and cosine functions. We can apply these formulas to express the product of trigonometric functions into sum and the difference of sine and cosine functions. In real life, we use Product to sum formula to simplify the expression in trignometric functions.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What are Product-to-sum/difference formulae?
2. Product into Sum/Difference Formulas
3. Proof of Product-to-sum formulae
4. Solved Example Based on Product to Sum/Difference

In this article, we will cover the concept of Product into Sum/Difference. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

What are Product-to-sum/difference formulae?

The Product formula is used to express the Product of sine and cosine functions into the sum or difference of sine and cosine functions. The sum and difference formulas of sine and cosine functions are added or subtracted to derive these identities. The product-to-sum identities can be used to simplify the trigonometric expression.

Product into Sum/Difference Formulas

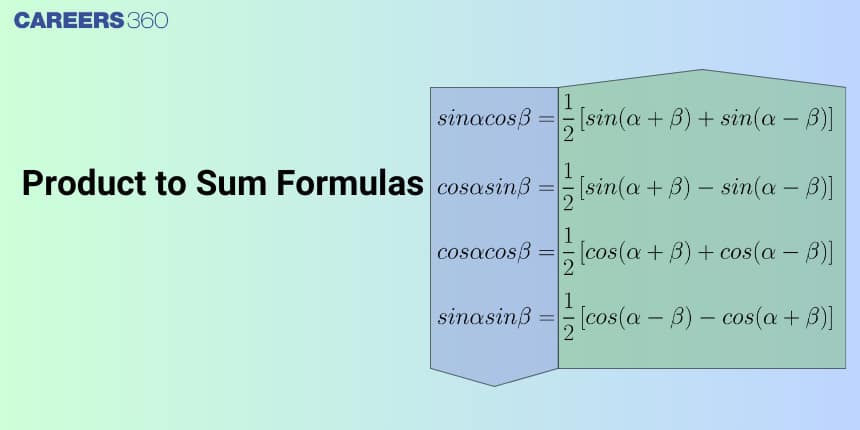
Product-to-sum formulas provide a powerful tool for simplifying trigonometric expressions involving products of sines and cosines, and the product to sum formulas are:

1. $2 \cos \alpha \cos \beta=[\cos (\alpha-\beta)+\cos (\alpha+\beta)]$
2. $2 \sin \alpha \sin \beta=[\cos (\alpha-\beta)-\cos (\alpha+\beta)]$
3. $2 \sin \alpha \cos \beta=[\sin (\alpha+\beta)+\sin (\alpha-\beta)]$
4. $2 \cos \alpha \sin \beta=[\sin (\alpha+\beta)-\sin (\alpha-\beta)]$

where, $\alpha$ and $\beta$ are two angles of a triangle
1) $2 \cos \alpha \cos \beta=\cos (\alpha-\beta)+\cos (\alpha+\beta)$

This formula involves the conversion of the product of cosine functions of two different angles into a sum of the cosine angle.
2) $2 \sin \alpha \sin \beta=\cos \left(\alpha-\beta\right)-\cos \left(\alpha+\beta\right)$

This formula involves the conversion of the product of sine functions of two different angles into a difference in the cosine angle.
3) $2 \sin \alpha \cos \beta=\sin (\alpha+\beta)+\sin (\alpha-\beta)$

This formula involves the conversion of the product of sine and cosine functions of two different angles into a sum of the sine angle.
4) $2 \cos \alpha \sin \beta=\sin \left(\alpha{+} \beta\right)-\sin (\alpha-\beta)$

This formula involves the conversion of the product of sine and cosine functions of two different angles into a different of sine angle.

Proof of Product-to-sum formulae

sin (A + B) = sin A cos B + cos A sin B ... (1)
sin (A - B) = sin A cos B - cos A sin B ... (2)
cos (A + B) = cos A cos B - sin A sin B ... (3)
cos (A - B) = cos A cos B + sin A sin B ... (4)

1. Deriving the formula sin A cos B = (1/2) [ sin (A + B) + sin (A - B) ]

Adding the equations (1) and (2), we get

sin (A + B) + sin (A - B) = 2 sin A cos B

Dividing both sides by 2,

sin A cos B = (1/2) [ sin (A + B) + sin (A - B) ]

2. Deriving the formula cos A sin B = (1/2) [ sin (A + B) - sin (A - B) ]

Subtracting (2) from (1),

sin (A + B) - sin (A - B) = 2 cos A sin B

Dividing both sides by 2,

cos A sin B = (1/2) [ sin (A + B) - sin (A - B) ]

3. Deriving the formula cos A cos B = (1/2) [ cos (A + B) + cos (A - B) ]

Adding the equations (3) and (4), we get

cos (A + B) + cos (A - B) = 2 cos A cos B

Dividing both sides by 2,

cos A cos B = (1/2) [ cos (A + B) + cos (A - B) ]

4. Deriving the formula sin A sin B = (1/2) [ cos (A - B) - cos (A + B) ]

Subtracting (3) from (4),

cos (A - B) - cos (A + B) = 2 sin A sin B

Dividing both sides by 2,

sin A sin B = (1/2) [ cos (A - B) - cos (A + B) ]

Product of cosines

$
\begin{array}{r}
\cos \alpha \cos \beta+\sin \alpha \sin \beta=\cos (\alpha-\beta) \\
+\cos \alpha \cos \beta-\sin \alpha \sin \beta=\cos (\alpha+\beta) \\
\hline 2 \cos \alpha \cos \beta=\cos (\alpha-\beta)+\cos (\alpha+\beta)
\end{array}
$

Product of sine and cosine

$
\begin{gathered}
\sin (\alpha+\beta)=\sin (\alpha) \cos (\beta)+\cos (\alpha) \sin (\beta) \\
+\sin (\alpha-\beta)=\sin (\alpha) \cos (\beta)-\cos (\alpha) \sin (\beta) \\
\hline \sin (\alpha+\beta)+\sin (\alpha-\beta)=2 \sin (\alpha) \cos (\beta)
\end{gathered}
$

Product of cosine

$
\begin{gathered}
\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta \\
-\quad \cos (\alpha+\beta)=-(\cos \alpha \cos \beta-\sin \alpha \sin \beta) \\
\hline \cos (\alpha-\beta)-\cos (\alpha+\beta)=2 \sin \alpha \sin \beta
\end{gathered}
$

Recommended Video Based on Product to Sum/Difference

Solved Example Based on Product to Sum/Difference

Example 1: The value of $
\cos \left(\frac{2 \pi}{7}\right)+\cos \left(\frac{4 \pi}{7}\right)+\cos \left(\frac{6 \pi}{7}\right)
$ is equal to? [JEE MAINS 2022]
Solution:

Using Summation of cosine series

$
\begin{aligned}
\cos \frac{2 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{6 \pi}{7} & =\frac{\sin 3 \times \frac{2 \pi}{2 \times 7}}{\sin \frac{2 \pi}{2 \times 7}} \times \cos \left(\frac{\frac{2 \pi}{7}+\frac{6 \pi}{7}}{2}\right)
\end{aligned} $

$\begin{aligned} & =\frac{\sin \frac{5 \pi}{7}}{\sin \frac{\pi}{7}} \times \cos \frac{4 \pi}{7} \\ & =\frac{\sin \left(\pi-\frac{4 \pi}{7}\right) \cos \frac{4 \pi}{7}}{\sin \frac{\pi}{7}}\end{aligned}$
$
\begin{aligned}
& =\frac{2 \sin \frac{4 \pi}{7} \cos \frac{4 \pi}{7}}{2 \sin \frac{\pi}{7}} \\
& =\frac{\sin \frac{8 \pi}{7}}{2 \sin \frac{\pi}{7}}=-\frac{1}{2}
\end{aligned}
$
Hence the answer is $1 / 2$

Example 2: The value of $\cos ^2 10^{\circ}-\cos 10^{\circ} \cos 50^{\circ}+\cos ^2 50^{\circ}$ is [JEE MAINS 2019]
Solution: $\cos ^2 10^{\circ}-\cos 10^{\circ} \cos 50^{\circ}+\cos ^2 50^{\circ}$

$
\begin{aligned}
& \Rightarrow \frac{1+\cos 20^{\circ}}{2}+\frac{1+\cos 100^{\circ}}{2}-\cos 10^{\circ} \cos 50^{\circ} \\
& \Rightarrow \frac{1}{2}\left[2+\cos 20^{\circ}+\cos 100^{\circ}-2 \cos 10^{\circ} \cos 50^{\circ}\right] \\
& \Rightarrow \frac{1}{2}\left[2+\cos 100^{\circ}+\cos 20^{\circ}-\cos 60^{\circ}-\cos 40^{\circ}\right] \\
& \Rightarrow \frac{1}{2}\left[\frac{3}{2}+2 \cos 60^{\circ} \cdot \cos 40^{\circ}-\cos 40^{\circ}\right] \\
& \Rightarrow \frac{1}{2}\left[\frac{3}{2}+2 \times \frac{1}{2} \cos 40^{\circ}-\cos 40^{\circ}\right]=\frac{3}{4}
\end{aligned}
$
Hence, the answer is $3 / 4$

Example 3: If $x+\frac{1}{x}=2 \cos \theta$, then $x^3+\frac{1}{x^3}$ ?
Solution

$
\begin{aligned}
&\left(x+\frac{1}{x}\right)^3=x^3+\frac{1}{x^3}+3 x \cdot \frac{1}{x}\left(x+\frac{1}{x}\right) \quad \because(x+y)^3=x^3+y^3+3 x y(x+y) \\
& x^3+\frac{1}{x^3}=\left(x+\frac{1}{x}\right)^3-3 x \cdot \frac{1}{x}\left(x+\frac{1}{x}\right) \quad \text { Given }\left(x+\frac{1}{x}\right)=2 \cos \theta \\
& x^3+\frac{1}{x^3}=(2 \cos \theta)^3-3 \cdot 2 \cos \theta \\
&=2\left[4 \cos ^3 \theta-3 \cos \theta\right] \\
&=2 \cos 3 \theta
\end{aligned}
$
Hence, the answer is $2 \cos 3 \theta$

Example 4: The value of $\sin \left(18^{\circ}\right)+\sin \left(72^{\circ}\right)-\sqrt{2} \cos \left(27^{\circ}\right)$ is
Solution

$
\begin{aligned}
& \sin \left(18^{\circ}\right)+\sin \left(72^{\circ}\right)-\sqrt{2} \cos \left(27^{\circ}\right) \\
& =2 \sin \left(45^{\circ}\right) \cos 27^{\circ}-\sqrt{2} \cos \left(27^{\circ}\right) \\
& =0
\end{aligned}
$
Hence, the answer is 0.

Example 5: if $\sin (3 x)+\sin (2 x)-\sin (x)=0$, then find the number of solutions in $[0, \pi]$ ?
Solution

$
\Rightarrow \sin (3 x)+\sin (2 x)-\sin (x)=0
$

$
\begin{aligned}
& \Rightarrow \sin (3 x)-\sin (x)+\sin (2 x)=0 \\
& \Rightarrow 2 \sin (x) \cos (2 x)+\sin (2 x)=0 \\
& \Rightarrow 2 \sin (x) \cos (2 x)+2 \sin (x) \cos (x)=0 \\
& \Rightarrow 2 \sin (x)\{\cos (2 x)+\cos (x)=0 \\
& \Rightarrow 2 \sin (x)\left\{2 \cos \left(\frac{3 x}{2}\right) \cos \left(\frac{x}{2}\right)\right\}=0 \\
& \Rightarrow x=0, \frac{\pi}{3}, \pi
\end{aligned}
$

Hence, the answer is the 3.