Section Formula in Vector Algebra - Definition, Formulas, Proof and Examples

A vector lying on the line formed by joining two vectors divides it into two parts externally or internally. Section formula is used to find the ratio in which the line segment is divided by the vector that lies externally or internally on a line. With the help of the section formula, we can also find the location of a vector from where the line is divided. In real life, we use section formulas in buildings and architectural design.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Section Formula?
2. Internal Section Formula
3. Derivation of Internal Section Formula
4. External Section Formula
5. Midpoint Formula
6. Solved ExamplesExample 1: If the vectors $=3 \hat{i}+4 \hat{k}$ and $\overrightarrow{A C}=5 \hat{i}-2 \hat{j}+4 \hat{k}$ are the sides of a triangle ABC, then the length of the median through A is: Solution: Midpoint formula - $\frac{\vec{a}+\vec{b}}{2}$ If $\vec{a}$ and, position vector of the mid-point of AB

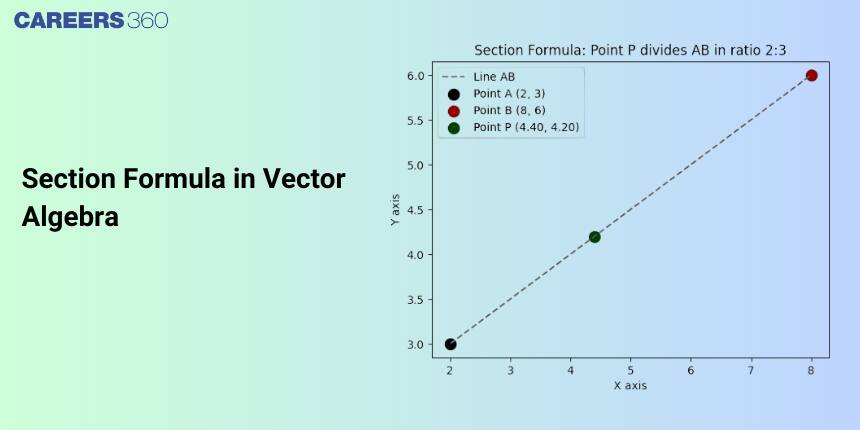
In this article, we will cover the concept of Section Formula. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of eight questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2013, and one in 2016.

What is Section Formula?

The section formula is the formula used for determining the coordinates of the vector that divides the line formed by joining the two vectors.

Let A and B be two points represented by the position vectors $\overrightarrow{O A}$ and $\overrightarrow{O B}$ respectively, with respect to the origin O.

Let R be a point that divides the line segment joining the points A and B in the ratio m: n.

Internal Section Formula

The internal division is the division of a line formed by joining two vectors by a vector lying between the two vectors.

If R divides AB internally in the ratio m: n, then the position vector of R is given by $\overrightarrow{\mathrm{OR}}=\frac{m \vec{b}+n \vec{a}}{m+n}$

Derivation of Internal Section Formula

Let $O$ be the origin. Then $\overrightarrow{\mathrm{OA}}=\tilde{\mathbf{a}}$ and $\overrightarrow{\mathrm{OB}}=\tilde{\mathbf{b}}$. Let $\tilde{\mathbf{r}}$ be the position vector of R which divides AB internally in the ratio $\mathrm{m}: \mathrm{n}$. Then

$
\begin{aligned}
& \frac{\mathrm{AR}}{\mathrm{RB}}=\frac{\mathrm{m}}{\mathrm{n}} \\
& \mathrm{n}(\overrightarrow{A R})=\mathrm{m}(\overrightarrow{R B})
\end{aligned}
$
Now from triangles ORB and OAR, we have

$
\overrightarrow{\mathrm{RB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OR}}=\tilde{\mathrm{b}}-\tilde{\mathrm{r}}
$
and, $\overrightarrow{\mathrm{AR}}=\overrightarrow{\mathrm{OR}}-\overrightarrow{\mathrm{OA}}=\tilde{\mathrm{r}}-\tilde{\mathrm{a}}$
Therefore, we have
$\mathrm{m}(\tilde{\mathrm{b}}-\tilde{\mathrm{r}})=\mathrm{n}(\tilde{\mathrm{r}}-\tilde{\mathrm{a}})$
or $\quad \vec{r}=\frac{m \vec{b}+n \vec{a}}{m+n}$

Hence, the position vector of the point R which divides A and B internally in the ratio of m: n is given by

$\overrightarrow{\mathrm{OR}}=\frac{m \vec{b}+n \vec{a}}{m+n}$

External Section Formula

The external section formula is used when the line segment is divided externally by the point in the given ratio. This formula is used to find the coordinates of the point on the line segment joining the two points and falling beyond the two points, in the given ratio.

If R divides AB externally in the ratio m: n, then the position vector of R is given by $\overrightarrow{\mathrm{OR}}=\frac{m \vec{b}-n \vec{a}}{m-n}$

Midpoint Formula

The midpoint formula is used to find the coordinates of the midpoint of a line segment. Here, the ratio between the two parts is 1:1. A midpoint refers to a point that is exactly in the middle of the line segment.

If R is the midpoint of AB, then m = n. And therefore, the midpoint R of $\overrightarrow{A B}$ , will have its position vector as $\overrightarrow{\mathrm{OR}}=\frac{\vec{a}+\vec{b}}{2}$

Solved Examples
Example 1: If the vectors $=3 \hat{i}+4 \hat{k}$ and $\overrightarrow{A C}=5 \hat{i}-2 \hat{j}+4 \hat{k}$ are the sides of a triangle ABC, then the length of the median through A is:
Solution: Midpoint formula - $\frac{\vec{a}+\vec{b}}{2}$
If $\vec{a}$ and, position vector of the mid-point of AB

$
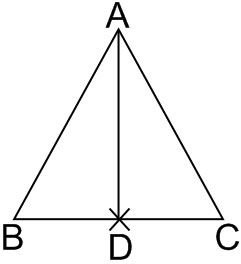
\frac{\overrightarrow{A B}+\overrightarrow{A C}}{2}=\overrightarrow{A D}
$
$
\begin{aligned}
& \overrightarrow{A D}=4 \vec{i}+\vec{j}+4 \vec{k} \\
& |\overrightarrow{A D}|=\sqrt{4^2+1^2+4^2}=\sqrt{33}
\end{aligned}
$
Hence, the answer is $\sqrt{33}$

Example 2: If $C$ is the midpoint of $A B$ and $P$ is any point outside $A B$, then
Solution: If $\vec{a}$ and $\vec{b}$, position vector of mid-point of $A B$

$
\begin{aligned}
& \overrightarrow{P A}+\overrightarrow{P B}=(-\vec{P}+\vec{a})+(-\vec{P}+\vec{b}) \\
= & -2 \vec{P}+(\vec{a}+\vec{b}) \\
\overrightarrow{P C}= & \frac{\vec{a}+\vec{b}-2 \vec{P}}{2} \\
= & \frac{\overrightarrow{P A}+\overrightarrow{P B}}{2} \\
= & \overrightarrow{P A}+\overrightarrow{P B}=2 \overrightarrow{P C}
\end{aligned}
$
Hence, the answer is $\overrightarrow{P A}+\overrightarrow{P B}=2 \overrightarrow{P C}$

Example 3: The position vector of the point, which divides the join of the points having position vectors $\hat{i}+2 \hat{j}+\hat{k}$ and $-\hat{i}-\hat{j}+2 \hat{k}$ internally in ratio $2: 1$ is:
Solution: Let $\vec{a}=\hat{i}+2 \hat{j}+\hat{k}, \vec{b}=-\hat{i}-\hat{j}+2 \hat{k}$
And $m: n=2: 1$

$
\therefore \vec{r}=\frac{1(\hat{i}+2 \hat{j}+\hat{k})+2(-\hat{i}-\hat{j}+2 \hat{k})}{1+2}=\frac{-\hat{i}+5 \hat{k}}{3}
$
Hence, the answer is $\frac{1}{3}(-\hat{i}+5 \hat{k})$

Example 4: The vectors $\overrightarrow{A B}=3 \hat{i}+4 \hat{k}$ and $\overrightarrow{A C}=5 \hat{i}-2 \hat{j}+4 \hat{k}$ are the sides of a triangle $A B C$. The length of the median through $A$ is
Solution

$
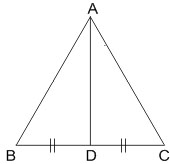
\begin{aligned}
& \text { Median is } \overrightarrow{A D}=\frac{\overrightarrow{A B}+\overrightarrow{A C}}{2} \\
& =\frac{3 \hat{i}+4 \hat{k}+5 \hat{i}-2 \hat{j}+4 \hat{k}}{2} \\
& =4 \hat{i}-\hat{j}+4 \hat{k}
\end{aligned}
$
Length of Median $=|\overrightarrow{A D}|=\sqrt{4^2+1^2+4^2}=\sqrt{33}$
Hence, the answer is $\sqrt{33}$

Summary

Section formula provides the precise method for solving the problem related to the division of line. Knowing the section formula equips one with a special tool for solving problems related to line division. With the help of the section formula, we can also find the centroid of a triangle, the centre of mass of the object, etc.