Semiperimeter And Half Angle Formulae

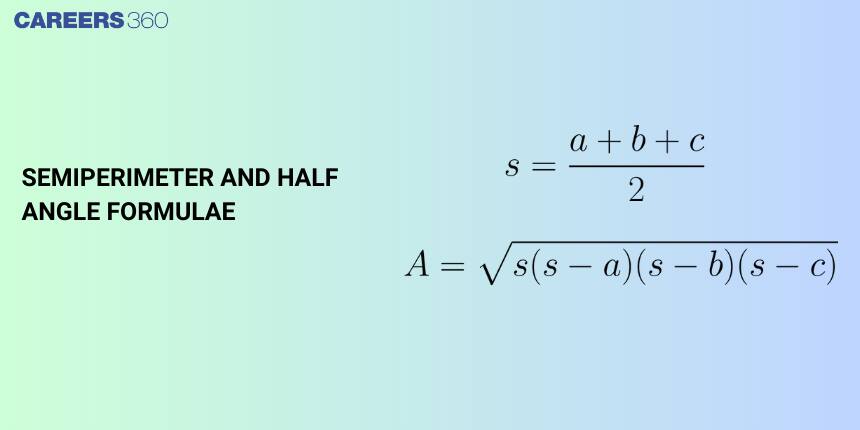
Semiperimeter Formula of a Triangle

The semiperimeter formula of a triangle is a simple but important concept in geometry and trigonometry. It is defined as half of the triangle’s perimeter and is denoted by $s=\frac{a+b+c}{2}$. This formula plays a key role in solving problems related to Heron’s formula, half-angle identities, and trigonometric relations in triangles.

Definition of Semiperimeter ($s = \frac{a+b+c}{2}$)

The semiperimeter formula of a triangle is the sum of all three sides divided by two. If the sides are $a$, $b$, and $c$, then
$s = \frac{a+b+c}{2}$.
This value is widely used in calculating area, inradius, and solving triangle-based problems in geometry.

Semiperimeter and Area Formula (Heron’s Formula)

Using semiperimeter, the area of a triangle can be calculated without directly using the height.
Heron’s Formula:
$A = \sqrt{s(s-a)(s-b)(s-c)}$
where $s$ is the semiperimeter.
This makes the semiperimeter and area formula very useful in trigonometry and geometry.

Semiperimeter and Inradius Formula ($A = r \cdot s$)

Another important relation is between semiperimeter and inradius. The area of a triangle can also be expressed as:
$A = r \cdot s$
where $r$ is the inradius of the triangle. This formula highlights the role of semiperimeter in circle-related problems inside triangles.

Applications of Semiperimeter Formula in Geometry

• Finding the area of any triangle when only sides are known.

• Deriving relations involving inradius and circumradius.

• Useful in problems involving incircle and excircle properties.

• Applied in advanced trigonometry for proving half angle identities.

Half Angle Formula in Trigonometry

The half-angle formulas can be derived from the double-angle or reduction formulas. They are useful when the given angle is half the size of a standard angle.

Half Angle Formula for Sin, Cos, and Tan

The half-angle formulas are written with a $\pm$ sign. This does not mean both positive and negative are valid simultaneously. The correct sign is chosen depending on the quadrant in which $\frac{\alpha}{2}$ lies.

1. $\sin \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 - \cos \alpha}{2}}$

2. $\cos \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 + \cos \alpha}{2}}$

3. $\tan \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 - \cos \alpha}{1 + \cos \alpha}}$

Derivation of Half-Angle Formula for Sine

Starting with the identity:

$\sin^2 \theta = \frac{1 - \cos (2\theta)}{2}$

Now replace $\theta$ with $\frac{\alpha}{2}$:

$\sin^2 \left(\frac{\alpha}{2}\right) = \frac{1 - \cos \alpha}{2}$

Taking square root:

$\sin \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 - \cos \alpha}{2}}$

Derivation of Half-Angle Formula for Cosine

Using the identity:

$\cos^2 \theta = \frac{1 + \cos (2\theta)}{2}$

Substitute $\theta = \frac{\alpha}{2}$:

$\cos^2 \left(\frac{\alpha}{2}\right) = \frac{1 + \cos \alpha}{2}$

Taking square root:

$\cos \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 + \cos \alpha}{2}}$

Derivation of Half-Angle Formula for Tangent

Start with:

$\tan^2 \theta = \frac{1 - \cos (2\theta)}{1 + \cos (2\theta)}$

Substitute $\theta = \frac{\alpha}{2}$:

$\tan^2 \left(\frac{\alpha}{2}\right) = \frac{1 - \cos \alpha}{1 + \cos \alpha}$

Taking square root:

$\tan \left(\frac{\alpha}{2}\right) = \pm \sqrt{\frac{1 - \cos \alpha}{1 + \cos \alpha}}$

Uses of Half Angle Formula in Solving Trigonometric Equations

• Simplifying higher power trigonometric functions.

• Converting equations into quadratic forms.

• Solving integration problems in calculus.

• Useful in problems involving exact values of non-standard angles.

Semiperimeter and Half Angle Formula Combined

The semiperimeter and half angle formula combined provides a strong link between geometry and trigonometry. Using the semiperimeter $s=\frac{a+b+c}{2}$, we can express the half-angle identities for sine, cosine, and tangent in terms of the triangle’s sides. This relation is especially useful in deriving formulas involving the inradius, area, and trigonometric ratios of a triangle.

How Semiperimeter and Half Angle Formula Work Together

The semiperimeter and half angle formula are often linked. In a triangle with sides $a, b, c$, we use:
$\sin^2 \frac{A}{2} = \frac{(s-b)(s-c)}{bc}$
$\cos^2 \frac{A}{2} = \frac{s(s-a)}{bc}$
These connect half angle identities with the semiperimeter.

Half Angle Formula Using Semiperimeter

In this section, we will see the half angle formulas using the semi perimeter. i.e., these are the half angle formulas in terms of sides of a triangle. Let us consider a triangle ABC where AB = c, BC = a, and CA = b.

We know that the semi-perimeter of the triangle is

$
s=\frac{a+b+c}{2}
$

From this, we have

$
2 s=a+b+c
$

Derivation of Half-Angle Formula for Cosine

$
\begin{gathered}
\cos A=2 \cos ^2\left(\frac{A}{2}\right)-1 \quad \text { (or) } \\
2 \cos ^2\left(\frac{A}{2}\right)=1+\cos A
\end{gathered}
$

Now using the law of cosines,

$
\begin{gathered}
2 \cos ^2\left(\frac{A}{2}\right)=1+\frac{b^2+c^2-a^2}{2 b c} \\
2 \cos ^2\left(\frac{A}{2}\right)=\frac{2 b c+b^2+c^2-a^2}{2 b c} \\
2 \cos ^2\left(\frac{A}{2}\right)=\frac{(b+c)^2-a^2}{2 b c} \\
2 \cos ^2\left(\frac{A}{2}\right)=\frac{(b+c+a)(b+c-a)}{2 b c} \\
2 \cos ^2\left(\frac{A}{2}\right)=\frac{2 s(2 s-2 a)}{2 b c} \\
2 \cos ^2\left(\frac{A}{2}\right)=\frac{2 s(s-a)}{b c} \\
\cos ^2\left(\frac{A}{2}\right)=\frac{s(s-a)}{b c} \\
\cos ^2\left(\frac{A}{2}\right)=\sqrt{\frac{s(s-a)}{b c}}
\end{gathered}
$

Similarly, we can derive other half-angle identities for cosine using the semi-perimeter.

Derivation of Half-Angle Formula for Sine

$
\sin ^2\left(\frac{A}{2}\right)=\frac{1-\cos A}{2}
$

Using the law of cosines:

$
\begin{gathered}
\sin ^2\left(\frac{A}{2}\right)=\frac{1}{2}\left[1-\frac{b^2+c^2-a^2}{2 b c}\right] \\
=\frac{1}{2} \cdot \frac{a^2-(b-c)^2}{2 b c} \\
=\frac{1}{2} \cdot \frac{(a+b-c)(a+c-b)}{2 b c} \\
=\frac{1}{2} \cdot \frac{(a+b+c-2 c)(a+b+c-2 b)}{2 b c} \\
=\frac{1}{2} \cdot \frac{(2 s-2 c)(2 s-2 b)}{2 b c} \\
=\frac{(s-b)(s-c)}{b c} \\
\Rightarrow \sin \left(\frac{A}{2}\right)=\sqrt{\frac{(s-b)(s-c)}{b c}}
\end{gathered}
$

Half-Angle Formula for Tangent

The half-angle formula for the tangent function can be derived using:

$
\tan \left(\frac{A}{2}\right)=\frac{\sin \left(\frac{A}{2}\right)}{\cos \left(\frac{A}{2}\right)}
$

Solving Triangle Problems Using Half Angle Identities and Semiperimeter

• Find unknown angles using side lengths.

• Compute area using both $s$ and half angle relations.

• Prove advanced trigonometric identities.

• Solve competitive exam questions involving semiperimeter and half angle formula together.

Solved Examples Based on Half-Angle Formula

Example 1: In triangle $A B C$ if $\tan \frac{A}{2}, \tan \frac{B}{2}, \tan \frac{C}{2}$ are in H.P. then the sides of triangle $A B C$ will be in.

Solution:

Half-Angle Formula (in terms of perimeter and sides of the triangle)

$
\begin{aligned}
& \tan \frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \\
& \tan \frac{B}{2}=\sqrt{\frac{(s-a)(s-c)}{s(s-b)}} \\
& \tan \frac{C}{2}=\sqrt{\frac{(s-a)(s-b)}{s(s-c)}}
\end{aligned}
$

Hence, the answer is sides of triangle $A B C$ will be in $A P$

Example 2: If in a triangle $\mathrm{ABC},(s-a)(s-b)=s(s-c)$ then angle C is equal to.
Solution: Half-Angle Formula (in terms of perimeter and sides of the triangle.

$
\begin{aligned}
& \tan \frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \\
& \tan \frac{B}{2}=\sqrt{\frac{(s-a)(s-c)}{s(s-b)}} \\
& \tan \frac{C}{2}=\sqrt{\frac{(s-a)(s-b)}{s(s-c)}}
\end{aligned}
$

$
\begin{aligned}
\tan \frac{C}{2} & =\sqrt{\frac{(s-a)(s-b)}{s(s-c)}} \because(s-a)(s-b)=s(s-c) \\
\tan \frac{C}{2}=1 & =\tan \frac{\pi}{4} \\
C & =\frac{\pi}{2}
\end{aligned}
$

Hence, the answer is angle C is $\frac{\pi}{2}$

Example 3: The value of $\tan \frac{B}{2} \tan \frac{C}{2}$ if $\mathrm{b}+\mathrm{c}=2 \mathrm{a}$, is.
Solution:

$
\begin{aligned}
& \tan \frac{B}{2} \tan \frac{C}{2} \\
& =\sqrt{\frac{(s-a)(s-c)}{s(s-b)}} \sqrt{\frac{(s-a)(s-b)}{s(s-c)}} \\
& =\frac{s-a}{s} \\
& =\frac{b+c-a}{a+b+c} \\
& =\frac{1}{3}
\end{aligned}
$

Hence, the answer is $\frac{1}{3}$

Example 4: In triangle ABC if $\tan \frac{A}{2}=\frac{3}{8}$ and $\tan \frac{C}{2}=\frac{8}{9}$ then sides $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are in
Solution:

$
\begin{aligned}
& \tan \frac{A}{2} \tan \frac{C}{2} \\
& =\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} \sqrt{\frac{(s-a)(s-b)}{s(s-c)}} \\
& =\frac{s-b}{b} \\
& =\frac{a+c-b}{a+b+c}=\frac{3}{9}
\end{aligned}
$

(since $\tan \frac{A}{2}=\frac{3}{8}$ and $\tan \frac{C}{2}=\frac{8}{9}$ )

$
\begin{aligned}
& \Rightarrow 3(a+c-b)=a+b+c \\
& a+c=2 b
\end{aligned}
$

$a, b, c$ are in A.P.
Hence, the answer is A.P

Example 5: In a $\triangle A B C \cot \frac{A}{2} \cdot \cot \frac{B}{2} \cdot \cot \frac{\mathrm{C}}{2}$ is equal to

Solution: Trigonometric Ratios of Functions -
$\operatorname{cosec} \theta=\frac{H y p}{O p p}$
$\sec \theta=\frac{H y p}{\text { Base }}$
$\cot \theta=\frac{\text { Base }}{\text { Opp }}$

- wherein
$
\begin{aligned}
& \cot \frac{A}{2} \cdot \cot \frac{B}{2} \cdot \cot \frac{C}{2} \\
& =\frac{s(s-a)}{\Delta} \cdot \frac{s(s-b)}{\Delta} \cdot \frac{s(s-c)}{\Delta} \\
& =\frac{s^3(a+b+c)}{\Delta^3}=\frac{s^2 \Delta^2}{\Delta^3}=\frac{s^2}{\Delta} \\
& =\left(\frac{\Delta^2}{r^2}\right) \times \frac{1}{\Delta}=\frac{\Delta}{r^2} \\
& \cot \frac{A}{2} \cdot \cot \frac{B}{2} \cdot \cot \frac{C}{2}=\frac{\Delta}{r^2}
\end{aligned}
$

Hence, the answer is $\frac{\Delta}{r^2}$

List of Topics related to Semiperimeter and Half Angle Formula

The following is a list of topics related to semiperimeter and half angle formula that covers key concepts, formulas, and applications in trigonometry and geometry. These topics will help in solving triangle-based problems, area calculations, and simplifying trigonometric expressions.

NCERT Resources

For a clear understanding of Trigonometric Functions, NCERT notes, solutions, and exemplar are the best resources. Below are the recommended NCERT materials for Chapter 3.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Semiperimeter and Half Angle Formula

This section provides practice questions based on semiperimeter and half angle formula to strengthen problem-solving skills. These questions help in applying formulas effectively and preparing for exams with confidence.

Semiperimeter and Half Angle Formulae - Practice Question MCQ

You can practice questions on the related topics by using the links shared below: